4]
(a)
Solve , write your answer to 3 significant digits.




SOLUTION

We want to isolate the unknown variable. Take the logarithm to the base 10
of both sides of the equation. We use base 10 because we can evaluate
logarithms to the base 10 (common logarithms) using handy calculators.
We could have also used logarithms to the base e (natural logarithms)
for the same reason. Either base will give us the same answer.











Using a calculator, we get .


The symbol is read "approximately equal to".


(b)
Solve , write your answer to 3 significant digits.




SOLUTION
To be different, this time let's use logarithms to be base e (natural logarithms)









(c)
Solve , write your answer to 3 significant digits.




SOLUTION
Let's use common logarithms (base 10) again.







Now put all the on one side of the equation, say, the left side.



Factor out the on the left side.




To get alone and finish the problem, divide the equation by the coefficient of .







(d)
Solve the formula for .




SOLUTION
Multiply the equation by to get rid of the fraction.







Continue to isolate the term involving .



Or



We just changed the order in which the equation is written in order to be able
to more easily read it. Multiply by so the left side becomes positive.





Or



We are almost there.
Take the natural logarithm (ln) of both sides of the equation.






Remember, .



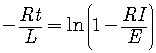
Finally, to get alone, multiply the equation by    .


Finished!



5]
Find the oblique asymptotes
(a)



SOLUTION
The graph of a rational functions (a fraction) has an oblique asymptote only if
the degree of the numerator is exactly one more than the degree of the denominator.
Do the long division.


                
              ____________
                            
                            
                           _____________
                                              

So


As , the remainder term , so the function behaves
more and more like , which is a linear function. The graph of a linear
function is a straight line, so the rational function has an oblique asymptote
whose equation is

.


(b)


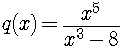
SOLUTION
The degree of the denominator, 5, is not one more than the degree
of the denominator, 3, so the function has no oblique asymptote.


(c)


SOLUTION



As , the remainder term , so the function has an oblique asymptote
whose equation is

.


6 ]
Find all vertical and horizontal asymptotes.
(a)


SOLUTION

The vertical asymptotes occur where the denominator of the rational function
is equal to zero.







The two vertical asymptotes are given by the equations

and .

To find the horizontal asymptote, if any, let us do the process:
Divide the numerator and the denominator of the fraction
by the highest power of the variable, viz., .



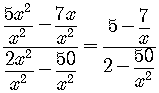
As , and
so


.

     is a finite number, so the function has an horizontal asymptote
          whose equation is

.


(b)



SOLUTION



The vertical asymptotes are the lines    and   .

Let's do the process to find the horizontal asymptotes:
The highest power is .




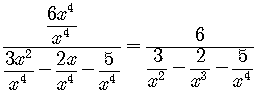
As , the denominator .

The numerator is a constant, 6, and the denominator is becoming smaller
and smaller towards zero, so the fraction itself is getting bigger and bigger,
blowing up towards infinity.
The conclusion is that the function does not have a horizontal asymptote.


(c)


SOLUTION
We must solve the equation

.

The polynomial on the left side involves only even powers of .
Raising a number to an even power always results in a number
that is positive or zero at the least.
The smallest value that

can take is

The denominator is never equal to zero.
Therefore, the function does not have a vertical asymptote.

For the horizontal asymptote, do the process. The highest power is .





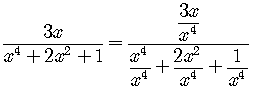
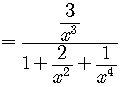
As



and

.
So



is a finite number, so the conclusion is that the function
has an horizontal asymptote whose equation is

.


                                                                            top

                                                                Review 2 Problems