7]
List all possible rational zeros.
(a)
SOLUTION
By the rational zeros theorem, if the equation has a rational zero,
,
the numeration must be an integer factor of the constant term
- here, the number 2 - and the denominator must be an integer factor
of the leading coefficient - here, the number 3.
The possible value of
are 
.The possible values of
are 
. So the possible rational roots are
.(b)
SOLUTION
The possible values of
.The possible values of
are 
.So the possible rational roots are
,
,
,
.8]
Find all roots exactly (rational, irrational, and imaginary) of the polynomial equation.
SOLUTION
The possible rational roots are
.Using synthetic division to test the numbers, we find
The third line is the result of the synthetic division.
The remainder which is the last number in the line is zero.
By the remainder theorem and the factor theorem,
is a root of the equation and 
is
a factor of the polynomial. The other factor is given by the numbers in the third line of the synthetic division.
These numbers are the coefficients of the second degree polynomial factor.
By the zero factors theorem, we set the quadratic factor equal to zero
in order to finish the solution of the problem.
Divide by
to simply the equation.
This equation can not easily be factored, so let's use the quadratic formula to solve it.
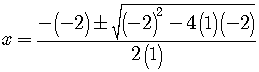
The three roots are
.9]
(a)
Use synthetic division and the remainder theorem to do this problem.
Find
, given 
.SOLUTION
By the remainder theorem,
.(b)
Using synthetic division, write the quotient including the remainder term.
SOLUTION
Put in the missing powers of
in the dividend. Synthetic division works when the divisor is of the form
,
so we must write
,
and 
is what goesinto the little box in the synthetic division scheme.
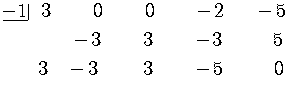
The quotient is given by the numbers in the third line.
The remainder
.(c)
Using synthetic division, write the quotient including the remainder term.
SOLUTION
Put in the missing powers of
in the dividend.Synthetic division works when the divisor is of the form
,
so
is what goes into the little box in the synthetic division scheme.
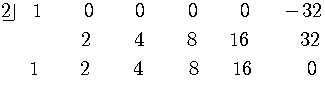
The quotient is given by the numbers in the third line.
The remainder
.10]
Sketch the graph of the functions. Indicate and label
the x-and y-intercepts, and the vertical, horizontal, and oblique asymptotes.
(a)
SOLUTION
vertical asymptotes
horizontal asymptote
oblique asymptote none
y-intercept is
set 
and solve
for 
x-intercept is
set 
and solve
for 
(b)
SOLUTION
vertical asymptotes are
and 
horizontal asymptote
oblique asymptote none
y-intercept
set
and solve for x-intercept
and 
set
and solve
for 
Multiply by the denominator to clear the fraction.
and 
top
End of Review 2
Review 2 Problems
© edmond 2002