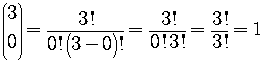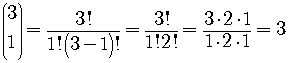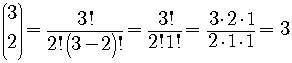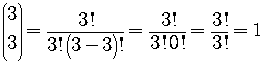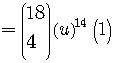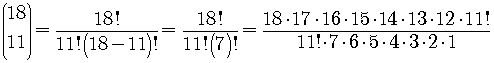1]
Use the binomial formula to expand


SOLUTION
The binomial formula is
, where is a positive integer.

The are called binomial coefficients.
They are defined by the formula

, where is the factorial symbol

and .

In particular, and .

For example, .

For our problem, we need to make the identifications  and  .

.

Note that the summation goes from 0 to 3 which is the power to which we are raising the binomial.


We must work out the powers and the values of the various binomial coefficients.








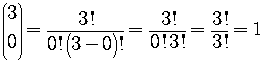
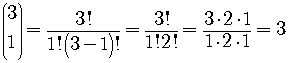
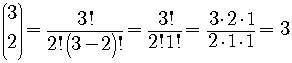
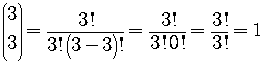
So


                               

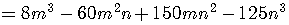
2]
Use the binomial formula to find the fifth and twelfth terms in the expansion of
         .

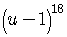SOLUTION
In the expansion for , the

.

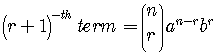The term is the term, so, and .


                             



            
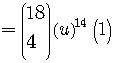
So



Similarly,




         
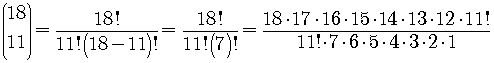
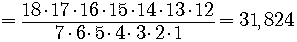
So



3]
a)
How many 4-letter code words are possible using the first 10 letters of the alphabet if
(i) No letter can be repeated?
(ii) Letters can be repeated?
(iii) Adjacent letters cannot be alike?

SOLUTION

(i) No letter can be repeated.
In a 4-letter code, there are 4 slots to fill.

___ ___ ___ ___

The first slot can be filled with any one of the 10 letters.

10 ___ ___ ___

Since no letters are to be repeated, only 9 letters are available in the second slot.

10 9 ___ ___

In the third slot only 8 letters are available.

10 9 8 ___

In the fourth slot only 7 letters are available.

10 9 8 7

By the Multiplication Principle, the number of 4-letters code is the product of the numbers.

10 x 9 x 8 x 7 = 5040

(ii) Letters can be repeated.
In each of the slots there are 10 possibilities, so the total number of possibilities.

= 10 x 10 x 10 x 10 = 10,000

(iii) Adjacent letters cannot be alike.
Fn the first slot there are 10 possibilities, for the second slot there are 9 possibilities.
For the third slot, the letter can be the same letter used in the second slot, so there are 10 - 1
or 9 possibilities for the third slot.
For the fourth slot, the letter can not be the same letters used for the third slot,
so there are still 10 - 1 or 9 possibilities for the fourth slot.

Then the number of codes = 10 x 9 x 9 x 9 = 7,290

b)
Find the number of permutations of 25 objects taken 8 at a time.
Compute the answer to 4 significant digits using a calculator.

SOLUTION
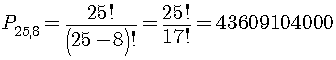exactly.
Rounding off to 4 significant digits and using scientific notation, the answer is

                                                                        

4]
a)
How many 4-letter code words are possible from the first 6 letters of the alphabet,
with no letter repeated? Allowing letters to repeat?

SOLUTION
With no letter repeated, the number of 4-letter codes = 6 x 5 x 4 x 3 = 360.
With letters allowed to be repeated, the number of 4-letter codes = 6 x 6 x 6 x 6 = 1296.

b)
How many different license plates are possible if each contains 3 letters followed by
3 digits? How many of these license plates contain no repeated letters and no repeated digits?

SOLUTION
With repetitions of letters and digits, the number of license plates
      = 26 x 26 x 26 x 10 x 10 x 10 = 17,576,000.

With no repeated letters and no repeated digits, the number of different license plates
      = 26 x 25 x 24 x 10 x 9 x 8 = 11,232,000


                                                            top

                                                    Problems Only


© edmond 2002