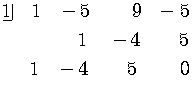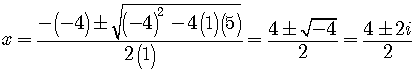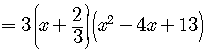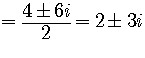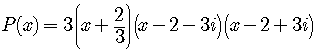14]
a)
Find all zeros exactly for .

SOLUTION
By the Rational Roots Theorem, the possible rational zeros of the polynomial are
.
Use synthetic division to test these possibilities.



So is a zero and is a factor of the polynomial by the factor Theorem.
Moreover,
.
Repeating this process, are the possible rational zeros of the polynomial
.
Again, use synthetic division to test these possibilities.


So is a zero of and we can write
.
The last factor is a quadratic polynomial.
We can use the quadratic formula to find its zeros.





The exact zeros of are .
The root , occurring twice, is called a root of multiplicity two.


b)
Given that and that is a zero,
write as a product of linear terms.

SOLUTION
Since is a zero of the polynomial, is a factor of the polynomial. To find the other factor, we use synthetic division.


So
.


To find the factors of the quadratic polynomial, we use the quadratic formula to solve the equation
.



So

and

are the factors of the quadratic polynomial.
Putting all these together, we write

.

This is the final answer.


15]
Find all vertical, horizontal, and oblique asymptotes. Do not graph.


SOLUTION
vertical asymptote
The verical aymptotes occur where the denominator is equal to zero.

is the equation of the vertical asymptote.

horizontal asymptote
To find the horizontal asymptote, we study the behavior of the function as .
Divide the numerator and the denominator of the fraction by the highest power of the variable, .



As , and .
The numerator remains constant, , while denominator gets smaller and smaller towards
zero, so the fraction itself gets bugger and bigger towarsd infinity. The fraction itself
blows up beyond all bounds.
Conclusion: The function does not have an horizontal asymptote.

oblique asymptote
The function has an oblique asymptote because the degree of the numerator is exactly
one more than the degree of the numerator. Now, we find the equation of the oblique asymptote by doing the division indicated in the function. We can use synthetic division.




As . the remainder term .
This means that the function behaves more and more like ,
which is a linear function and the graph of a linear function is a straight line, so
has a linear asymptote whose equation is
.


16]
Solve and check.

NOTE:
Recall that means , which are called common logarithms. The base is 10.

SOLUTION
Use the laws for working with logaithms. We can write the left side of the equation as the
logarithm of a product.

By the definition of logarithms, this means
.
Solve this quadratic equation.





CHECK

does not work in the original, logarithmic equation because we get
and we can take the logarithm of a negative number.
In interval notation, the domain of the logarithmic function is .
In inequality notation, the domain is .
In set-builder notation, the domain is .


is this a true statement?
The left side



So we have the statement

which is true.
Conclusion: is the solution of the logarithmic equation.


17]
Solve the equations and give your answers to 3 significant digits.
a)


NOTE:
Recall that and that means .
Logarithms to the base are called natural logarithms.

SOLUTION
a)
Take the natural logarithm of both sides of the equation.


Use the laws for working with logarithms. The logarithm of a power is the power times the
logarithm.



This is just a linear equation in . We know how to solve linear equations.




b)


SOLUTION
Take the common logarithm of both sides of the equation.


Now us the property: The logarithm of a power is the power times the logarithm.




                                                top

                                        Problems Only


© edmond 2002