18]
Graph
SOLUTION
vertical asymptotes
To find the vertical asymptotes we find where the rational function is undefined,
that is, where the denominator of the rational function is zero
We need to solve the equation
So the vertical asymptotes are the vertical lines
and 
y intercepts
To find the y-intercepts, if any, we set x = 0 and solve the resulting equation for y
In this case, it's very easy
Remember that the function values of f(x) are the same as the y values
The coordinates of a point can be written as either (x, y ) or ( x, f(x) )
The y-intercept is the point
x intercepts
To find the x-intercepts, if any, we we set y = 0 and solve the resulting equation for x
We must solve the rational equation
The fraction on the left side of the equation is already reduced to lowest terms
In other words, there are no common factors in the numerator or the denominator
that can be cancelled to simplify the fraction
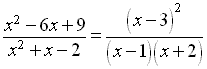
So the fraction will be equal to zero when the numerator is equal to zero
The solutions of this quadratic equation are
and The numbers are the same so the solution defines only one geometric point
So the x-intercept of the rational functions occurs only at the single point
horizontal asymptotes
To find the horizontal asymptotes, if any, of the rational function, we must examine
its behavior as the x coordinate of a point P(x,y) on the graph increases beyond all bounds.
In other words, as
Our method to do this - to examine the behavior of the rational function - is to divide
the numerator and denominator of the rational function by the highest power of the
variable x occurring in the rational function
Namely,
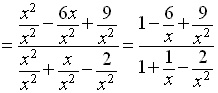
Now as
,
so
The limit
is a finite
number, so our conclusion is that the graphhas a horizontal asymptote and the equation of the horizontal asymptote is
Now to situate where the graph is located, we evaluate the function
at a single point in each of the subintervals
If the function is positive (negative) at one point in the subinterval,
it is positive (negative) everywhere
in the subinterval
What point we choose is arbitrary, any point will do and we are interested
only in the sign, + or - , of the evaluation
A positive ( + ) value means that the graph, within the chosen subinterval,
lies above the x-axis
A negative ( - ) value means that the graph, within the chosen subinterval,
lies below the x-axis
Graph of the Rational Function
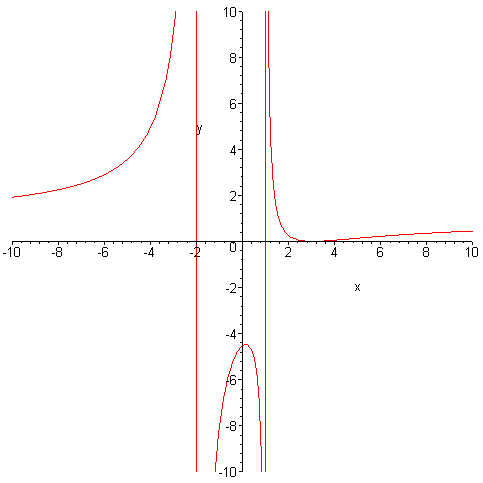
The vertical lines are the vertical asymptotes
19]
Simplify the complex fraction
SOLUTION
First, let's rewrite the fraction using only positive exponents
Remember the definition of negative exponents as reciprocals
In general,
So
To simplify a complex fraction, our method is to multiply
the numerator and the denominator of the complex fraction
by the LCD of the constituent fractions within the complex fraction
In this case,
It is important to use the parentheses,as shown above, in order to remind us
that we must use the Distributive Property
in algebra whenever we multiply
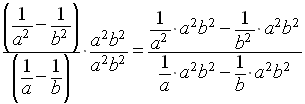
Now we must factor, if possible, the numerator and the denominator in order to see
whether we can simplify the fraction by canceling out factors that are common to both
the numerator and the denominator
Remember the difference of two squares identity
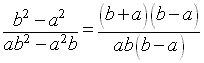
So the final answer is
20]
Write in standard form the complex fraction
,
where 
.SOLUTION
We must rewrite the fraction in the standard form for complex numbers, a + bi
Multiply the numerator and the denominator by the complex conjugate of the
denominator
The complex conjugate of
is 
The product in the denominator is in the difference of two squares form
The numerator is multiplied out using, as always, the distributive property
This is not yet in the standard complex number form, a + bi
We must rewrite the single fraction above as two fractions
with the common denominator of 5,
is the final answertop
Problems Only
©edmond 2002