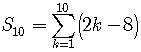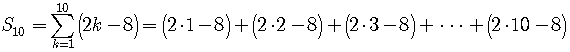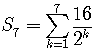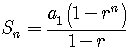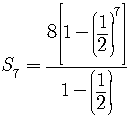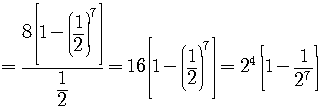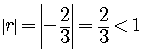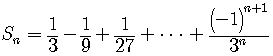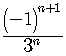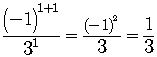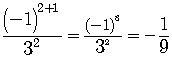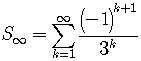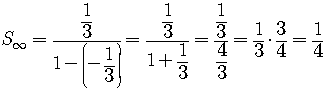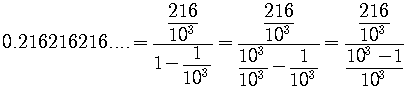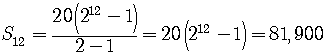5]
a)
Write the following without the summation notation and find the sum.


SOLUTION
Write out the first few terms of the series.


The sum begins at and ends at .
Determine whether the series is a geometric series or an arithmetic series.
If the difference between any two adjacent terms is a constant (always the same number),
then the series is an arithmetic series.
If the ratio of any two adjacent terms is a constant (always the same number),
then the series is a geometric series.
Do the arithmetic to get the terms of the series.



Let's apply the first test to determine whether the series is geometric or arithmetic.
Find the difference between any two adjacent terms.


etc.

The difference is always the same number, , so the series is an arithmetic series.
We can use either the formula
or to find the sum.
Let's use the first formula because we know , , .


b)

SOLUTION
As in the last problem, let's write out the first few terms of the series.

Determine whether the series is geometric or arithmetic.
Find the ratio of any two adjacent terms.




etc.
The ratio is always the same number, , so the series is geometric.
Use the formula



for the sum of the first terms of a geometric series.
Here,

, , .



Simplify and work out this complex fraction.









c)


SOLUTION
The means that the series is infinite. It goes on forever, never ends.
Test whether the series is geometric or arithmetic.
Find the ratio of any two adjacent terms.





etc.

The ratio is always the same number, . The series is a geometric series.

Since the absolute value of the common ratio is less than one

we know that the infinite geometric series converges and the sum is given by the formula

.




d)
Write

using summation notation, and find .

SOLUTION
The last term


is also the general term of the series.
It give the rule for forming the specific, individual terms of the series.
For example, to get the first term of the series put .

To get the second term of the series put .


So we can write the series in summation notation as

.
This is a geometric series with common ratio , so the infinite geometric series

converges and we can use the formula

to find the sum, as we did in the last problem.




6]
Represent the repeating decimal as the quotient of two integers.


SOLUTION
Note that we can write

The easiest way to do this problem is to find a fraction that represents the repeating decimal part

To see how this repeating decimal part is formed, we can write it column-wise as


Now write each term in the above sum as a fraction.
For example,






etc.

So

This is an infinite geometric series with the first term and the common ratio
, so the infinite series converges and its sum is given by the formula

.







So

is the answer.

7]
Let be a geometric sequence. Find the the indicated quantity.


SOLUTION
The sum of the first terms of a geometric series is given by the formula
.
Here, .



                                                      top

                                             Problems Only

© edmond 2002