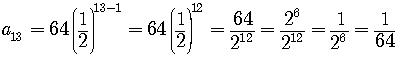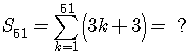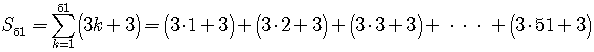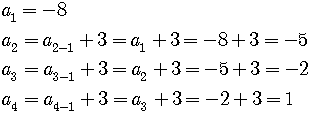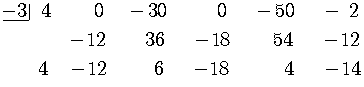8]
Let  be an geometric sequence. Find the indicated quantity.

                                                      

SOLUTION
The n-th term of a geometric sequence is given by the formula
.

Here, .




9]
Find


SOLUTION
Write out the first few terms of the series.



        
The difference between any two adjacent terms



etc.

is always the same number, , so the series is arithmetic and the sum of the first n terms is given by

or .

Since we know the first term and the last term and ,

.


10]
Let    be an arithmetic sequence. Find the indicated quantity.

                                                           

SOLUTION
The n-th term of an arithmetic sequence is given by the formula





means the sum of the first 12 terms of the arithmetic series,

.

We can use the formula

.




11]
Given  

(i) Write the first four terms of the sequence.
(ii) Find .
(iii) Find .

Note:
This is an example of a sequence in which the definition of the general term is given recursively.
That is, a term is defined by reference to another term.
In this case, is defined by reference to the previous term, .

(i) Write the first four terms of the sequence.
SOLUTION



(ii) Find .
SOLUTION
The sequence is an arithmetic sequence with common difference .
The n-th term of an arithmetic sequence is given by the formula

.




(iii) Find .

SOLUTION
is the sum of the first 10 terms of the arithmetic sequence.
The sum of the first n terms of an arithmetic series is given by the formula

.




12]
Use synthetic division to find the quotient and remainder resulting from dividing
  by   .

SOLUTION
Synthetic division works only when the divisor of the form ,
which is the case in this problem but we have to re-write
,  so  .
And we must re-write the polynomial to show the missing powers of .



Now we can correctly form the scheme for synthetic division.


The answer is read from the numbers in the last line of the synthetic division scheme.

The quotient is

and the remainder is .

So the answer to the long division problem is

.


13]
Find all the rational zeros for  .

SOLUTION
By the Rational Roots Theorem, if the polynomial has a rational root
,
the numerator must be a divisor of the constant term 6 and the denominator
must be a divisor of the leading coefficient 2.
The possible values of are

.
The possible values of are

.
The possible rational roots of the polynomial are

.

Now we use synthetic division to find if any of the possibilities listed
are roots of the polynomial.
We find that the rational roots are .

In fact, we have found all the roots of the polynomial
since the polynomial is of the 3^rd degree and has only three roots.


                                                 top

                                          Problems Only


© edmond 2002