Circular
Functions
Here we give a more abstract, modern approach to the definition
of trigonometric functions, which does not directly involve triangles
or angles. This enables us to employ trigonometric functions even in
cases where no angles are involved
In the Cartesian coordinate system the graph of
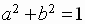
is a unit circle with center at the origin and radius 1
Using this circle, we define the circular functions on a domain of real numbers.
Let

be an arbitrary real number and let U be the unit circle
Begin at (1,0) and go counterclockwise along the circumference of the circle if

is positive and go clockwise along the circumference of the circle if  is negative,
is negative,
go until the an arc length of

along the circumference of the circle has been covered
Let P(a,b) be the point at the terminal end of the arc
DEFINITION 1
The six circular functions (commonly referred to as trigonometric functions)
are then defined in terms of the coordinates of the point P

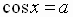

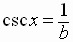
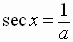
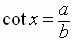
Notice that these definitions do not involve the mention of any angles.
The definitions involve the length of the arc whose measure is  ,
a real number,
,
a real number,
and the coordinates a and b of the point P that is the end-point of the arc.
Sine
and Cosine Domain and Range

By Definition 1, note that the coordinates of the point P at the end of an arc
of length
 ,
,
starting at (1,0), can be written as P(cos x, sin x).
The domains of the sine and the cosine functions, that is, the quantities for
which these functions
are defined, are real numbers.
Notice that as the point P moves around the circle the values of the sine and
the cosine functions
vary from –1 at the smallest to +1 at the largest;
these values comprise the range of the sine and the cosine functions.
Domain:
The set of all real numbers
Range:
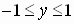 y
is a real number
y
is a real number
where 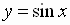 or
or 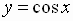
See
Example 1, pages 456 – 457, of the textbook.
Periodic
Functions
Imagine the point P moving around the unit circle in either direction, clockwise
or counterclockwise.
Every time P covers a distance of
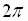
(the circumference of the unit circle), it will be back at the point where it
started.
So for any real number  and any integer
and any integer 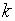 ,
it will be true that
,
it will be true that
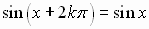
and
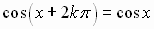
Functions with this kind of repetitive behavior are called periodic functions.
DEFINITION
A function 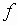 is periodic
if there exists a positive real number
is periodic
if there exists a positive real number 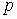 such that
such that
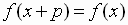
for all  in the domain
of
in the domain
of 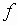 .
.
The smallest such positive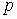 ,
if it exists, is called the fundamental period
,
if it exists, is called the fundamental period
of 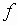 , or simply the
period of
, or simply the
period of 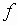 .
.
The sine and the cosine functions are periodic with period
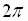 .
.
The other trigonometric functions also are periodic functions.
The tangent and the cotangent functions have period
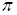 .
.
The secant and the cosecant functions have period
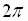 .
.
We will graph these functions in sec 6.6
See Example 2, page 458, of the
textbook.
Many phenomena in nature can be modeled using trigonometric functions
because of the periodic properties of the trigonometric functions.
For example, phenomena such as light, sound, and electromagnetic waves in general;
the motion of bridges and buildings during earthquakes; the motion of planets
and satellites.
Basic
Identities
From the definitions of the trigonometric functions, the following identities
are immediate.
For any real number  (restricted
so that both sides of the equation are defined):
(restricted
so that both sides of the equation are defined):
Reciprocal
Identities

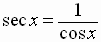

Quotient
Identities
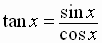
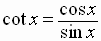
Identities
for Negatives



Pythagorean
Identity
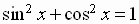
From the definitions of the circular functions (definition 1) and that

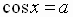
we can easily prove the identities.


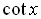

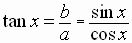
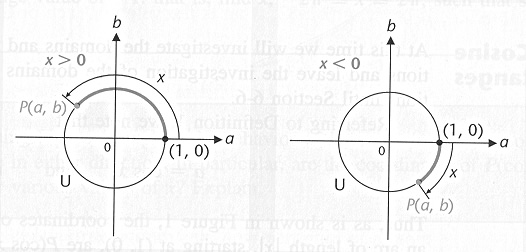
In the figure below, since the terminal points of x and -x are
symmetric with respect to the horizontal axis,

we can write:
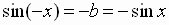
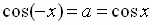
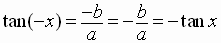
To prove the Pythagorean identity, note that

is on the unit circle
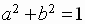
so that
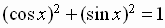 .
.
This is usually written in the form
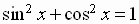
See Example 3, page 460, of the textbook.
Circular
Functions and Trigonometric functions
The definitions of the trigonometric functions involving angle domains can be
related to the circular
functions involving real number domains.
Look at the radian measure of an angle
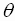
opposite an arc of  units on the unit circle.
units on the unit circle.

For the unit circle, the angle opposite an arc of  units has a radian measure of
units has a radian measure of  .
.
In other words, every real number  can
be associated with an arc of
can
be associated with an arc of  units on the
units on the
unit circle or a central angle of  radians on the same circle.
radians on the same circle.
If  is positive, go
counterclockwise;
is positive, go
counterclockwise;
if  is negative, go
clockwise.
is negative, go
clockwise.
Note that the point on the terminal end of the arc of  units is
units is
also on the terminal side of the angle of  radians,
so we can write the following relationships
radians,
so we can write the following relationships
between trigonometric functions defined with angle domains and the trigonometric
functions defined
with real number domains:
Circular
Functions
Trigonometric Functions
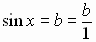
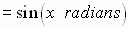
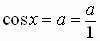
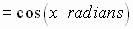
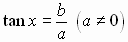

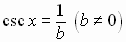

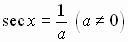
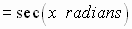
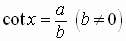

See
Examples 4 – 5, pages 461 – 462, of the textbook.
top
next Graphing
Basic Trigonometric Functions




