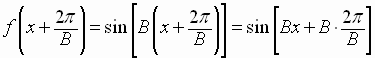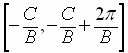Graphing 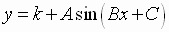 and
and 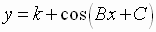
Functions of this form can be graphed by studying the effects of k,
A, B, and C
on the basic graphs of y = sin x and y = cos x.
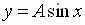 and
and 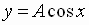
The constant
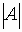
is called the amplitude of the graph .
Both graphs are periodic with period 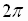 ,
since
,
since
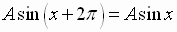
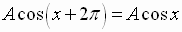
See Example 1, page
478, of the textbook.
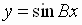 and
and 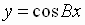
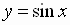 and
and 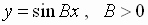 both have amplitude
equal to 1.
both have amplitude
equal to 1.
The period of the sine function is 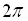 ,
,
so 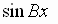 completes
one cycle as
completes
one cycle as 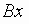 varies
from
varies
from
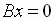 to
to 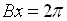
or, in other words, as 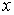 varies from
varies from
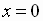 to
to 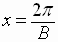
So the period of 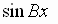 is
is
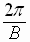
Checking:
If 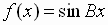 , then
, then
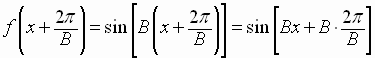
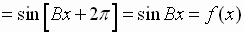
Similarly, the period of
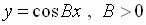
is
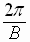
See Example 2, page
479, of the textbook.
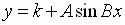 and
and 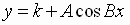
Summarizing
our results so far:
For 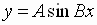 or
or 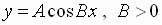
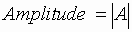
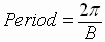
If 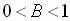 ,
,
the basic sine or cosine curve is stretched.
If 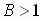 ,
,
the basic sine or cosine curve is compressed.
See Examples 3 – 4, pages 480 – 481, of the textbook.
The graphs of 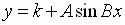 and
and
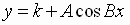
can be obtained by
translating
the graphs of
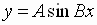 and
and
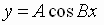
vertically,
up
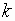 units
units
if
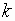 is positive
is positive
and
down
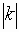 units
units
if
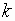 is negative.
is negative.
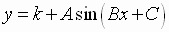 and
and 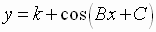
Since 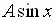 has period
has period
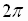 ,
,
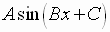
must complete one cycle as
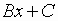
varies
from
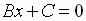
to
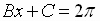
In other words, as
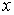
varies
from
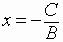
to
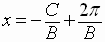
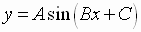 has a period of
has a period of 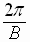
Its graph is translated
 units to the right if
units to the right if 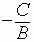 is positive
is positive
 units to the left if
units to the left if 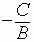 is negative
is negative
The quantity 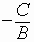 is
called the phase shift.
is
called the phase shift.
Similar results apply to 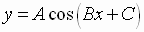
Summary of Properties of y = A sin (Bx + C) and
y = A cos (Bx + C)
For B > 0:
Amplitude = 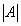 Period =
Period = 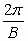 Phase Shift =
Phase Shift = 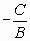
The graph completes one full cycle as 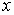 varies over the interval
varies over the interval
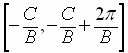
See Examples 6 – 8, pages 485 – 487, of the textbook.
top
next Graphing
General Tangent, Cotangent, Secant, and Cosecant Functions