Inverse
Trigonometric Functions
Here is a short review of the general concept of inverse functions
For  a one-to-one
function and
a one-to-one
function and  its
inverse
its
inverse
1]
If 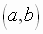 is an element of
is an element of  ,
then
,
then 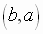 is an element
of
is an element
of  , and conversely
, and conversely
2]
Range of  = Domain of
= Domain of 
Domain of  = Range of
= Range of 
3]

4]
If 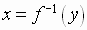 , then
, then 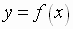 for
for 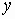 in the domain of
in the domain of 
and 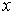 in the domain of
in the domain of  ,
and conversely
,
and conversely

5]
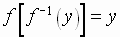 for
for 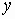 in the domain
of
in the domain
of 
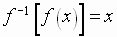 for
for 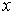 in the domain
of
in the domain
of 
The trigonometric functions are periodic
All of the trigonometric functions fail the horizontal line test
That is, each value in the range can be associated with infinitely many values
in the domain
So no trigonometric function is a one-one function
That is, no trigonometric function has an inverse function
However, if we restrict the domain of each function so that the function is a
one-one function
over the restricted domain, then we can define an inverse function over the restricted
domain
Inverse
Sine Function
The inverse sine function, denoted by 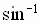 or
or 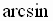 ,
,
is defined as the inverse
of the restricted sine function
 ,
, 
So
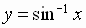 and
and

are equivalent to

where  ,
, 
In other words, the inverse sine of  ,
or the arcsine of
,
or the arcsine of  ,
,
is the number or angle 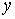 ,
,
 ,
,
whose sine is 

Sine-Inverse Sine Identities
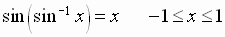

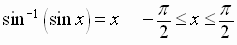

See Examples 1 – 2, pages 504 – 505, of the textbook
Inverse Cosine Function
The inverse cosine function, denoted by 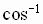 or
or 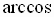 ,
,
is defined as the inverse
of the restricted cosine function
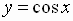 ,
, 
So
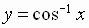 and
and

are equivalent to

where 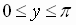 ,
, 
In other words, the inverse cosine of  ,
or the arccosine of
,
or the arccosine of  ,
,
is the number or angle 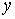 ,
,
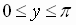 ,
,
whose cosine is 

Cosine-Inverse Cosine Identities


See Examples 3 – 4, pages 507 – 508, of the textbook.
Inverse Tangent Function
The inverse tangent function, denoted by  or
or
 ,
,
is defined as the inverse
of the restricted tangent function
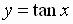 ,
, 
So
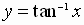 and
and 
are equivalent to

where

and  is a real number
is a real number
In other words, the inverse tangent of  ,
or the arctangent of
,
or the arctangent of  ,
,
is the number or angle 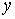 ,
,
 ,
,
whose tangent is 

Tangent-Inverse Tangent Identities


See Example 5, pages 509 – 510, of the textbook.
Inverse
Cotangent, Secant, and Cosecant Functions
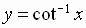 is equivalent to
is equivalent to 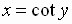 where
where 
 is equivalent to
is equivalent to 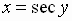 where
where 
 is equivalent to
is equivalent to  where
where 
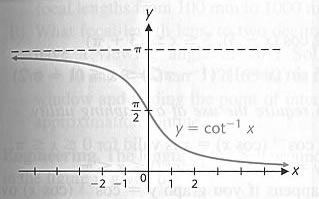
Domain:
All real number
Range: 
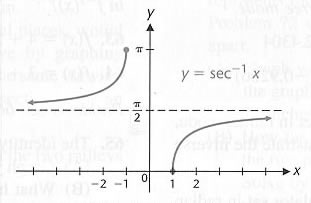
Domain:

Range: 

Domain: 
Range:
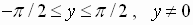
Note:
The definitions of 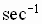 and
and 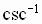 are not universally
agreed upon.
are not universally
agreed upon.
top
next Basic
Trigonometric Identities and Their Use
begin
Module 2
Trigonometric
Identities and Conditional Equations






