Double-Angle
and Half-Angle Identities
Double-Angle
Identities
Letting 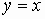 in the identity
in the identity
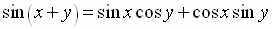
we get the
double-angle identity
for the sine function
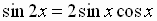
Similarly, letting 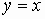 in the identity
in the identity

we get the
first
double-angle identity for the cosine function
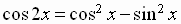
Using the Pythagorean identity

we get the
second
double-angle identity for the cosine function
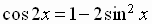
and the
third
double-angle identity for the cosine function,
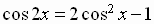
Since the tangent is the ratio of the sine to the cosine, and using the above
identities, and some simple algebra, we get the various forms of the
double-angle
identity for the tangent function
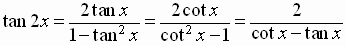
See Examples 1 – 2, pages 544 – 545, of the textbook.
Half-Angle
Identities
The half-angle identities are just the double-angle identities given in a different
form.
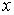 can be written
as
can be written
as 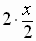
For example, the double-angle identity

can be rewritten as

or

Solving this equation for 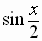 ,
we get the
,
we get the
Half-Angle Identity
for the Sine Function
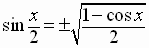
where the sign, 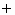 or
or
 , is determined by the quadrant
in which
, is determined by the quadrant
in which 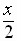 lies.
lies.
Similarly we get the
Half-Angle Identity
for the Cosine Function

where the sign, 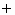 or
or
 , is determined by the quadrant
in which
, is determined by the quadrant
in which 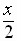 lies.
lies.
Since the tangent is the ratio of the sine to the cosine, we get the
Half-Angle Identity
for the Tangent Function
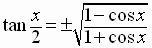
where the sign, 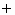 or
or  ,
is determined by the quadrant in which
,
is determined by the quadrant in which 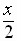 lies.
lies.
Other half-angle identities for the tangent function are

and
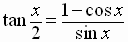
See Examples 3 – 5, pages 548 – 549,
of the textbook
top
next Product-Sum
and Sum-Product Identities