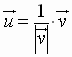Algebraic Vectors
By placing geometric vectors in the context of a rectangular coordinate system,
we can think of vectors in an algebraic way
Then we can employ all the operations of algebra to work abstractly with vectors
and use vectors in the solutions of problems
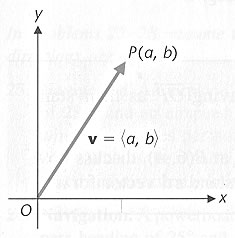
We will denote a vector by putting an arrow over the symbol
For example, in the figure above, the boldface vector will be written as 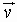
See Example 1, page 604, of the textbook
The magnitude, or norm, of a vector 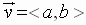 is given by
is given by

See Example 2, page 605, of the textbook
Vector
Addition
If 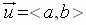 and
and
 , then
, then

Scalar
Multiplication of a Vector
If 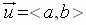 and
and
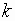 is a
scalar, then
is a
scalar, then

See Example 3, page 606, of the textbook
Unit
Vectors
A vector whose magnitude, or norm, is equal to 1 is called a unit vector
If  is
a nonzero vector, then
is
a nonzero vector, then
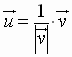
is a unit vector with the same direction as 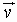
See Example 4, page 607, of the textbook
The
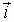 and
and 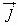 unit vectors.
unit vectors.

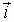 is a unit vector parallel to the x-axis
is a unit vector parallel to the x-axis
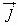 is a unit vector
parallel to the y-axis
is a unit vector
parallel to the y-axis
These unit vectors are important because any vector

can be written as a linear combination of these two vectors

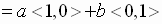
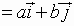
See Examples 5, page 608, of the textbook
Summary of Properties
For all vectors 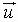 ,
,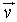 ,
, 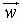 and
all scalars
and
all scalars 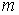 and
and
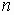 ,
,
the following properties hold
Addition Properties
1. 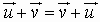 Commutative Property
Commutative Property
2. 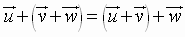 Associative Property
Associative Property
3. 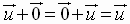 Additive
Identity
Additive
Identity
4. 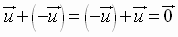 Additive
Inverse
Additive
Inverse
Scalar Multiplication
Properties
1. 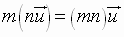 Associative
Property
Associative
Property
2. 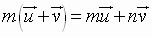 Distributive
Property
Distributive
Property
3. 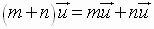 Distributive
Property
Distributive
Property
4. 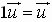 Multiplicative
Identity
Multiplicative
Identity
See Example 6, page 609, of the textbook
Static Equilibrium – see Example 7, pages 609 – 610, of the textbook
top
next Polar
Coordinates and Graphs