Law
of Sines
Oblique triangles – triangles without a right angle – can be
solved
by using the law of cosines or the law of sines
An oblique triangle is either acute (all the interior angles are between
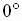 and
and 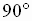 )
)
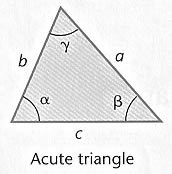
or obtuse (the triangle has an interior angle that is between 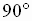 and
and 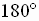 )
)
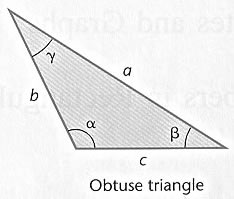
In any triangle there are three angles and three sides, six quantities in all
Given any three of the six quantities, we want to determines the measures
of the remaining three quantities
The processing of doing so is called solving the triangle
If the three given quantities include a side and the angle opposite the given
side,
the law of sines should be used in solving the triangle;
otherwise, the law of cosines should be used
The
Law of Sines
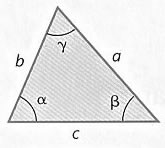
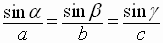
The
ratio of the sine of an angle to the side opposite the angle
is
the same as the ratio of either of the remaining angles to its opposite side
The ratios can be calculated when an angle of a triangle and the side opposite
the angle are known,
that is, their measures are given
So if one other part of the triangle is known, either another angle
or another side, then the quantity opposite that given part can be
calculated using the law of sines
The law of sines is used to solve triangles
when
1] Two sides and and an angle opposite one of the sides are given (SSA)
or
2] Two angles and any side are given (ASA or AAS)
CAUTION:
For a triangle, if two sides and the included angle (SAS) are give or three sides
(SSS)
are given, then the law of sines cannot be used to solve the triangle
For these cases, the law of cosines
may be used
SSA
Variations
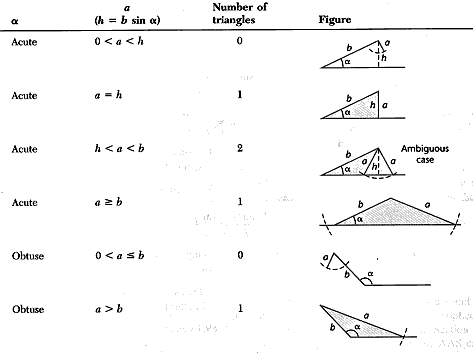
The ambiguous case occurs when 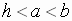 .
See the figure above
.
See the figure above
In this case, two solutions - two triangles - are always possible, , one an acute
triangle
and the other an obtuse triangle
Solving the ASA Case –see Example 1, pages 580 – 581, of the textbook
Solving the SSA Case – see Example 2, pages 582 – 583, of the textbook
Solving the Ambiguous SSA Case – see Example 3, pages 583 – 584, of
the textbook
Solving the AAS Case – see Example 4, pages 584 – 585, of the textbook
top
next Law of Cosines



