Conic Sections Parabola
Equation of the first degree in two variables
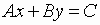
where the coefficients are not both zero have graphs that are straight lines
Equations of the second degree in two variables
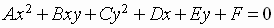
where the coefficients A, B and C are not all zero have graphs that are called
conic sections
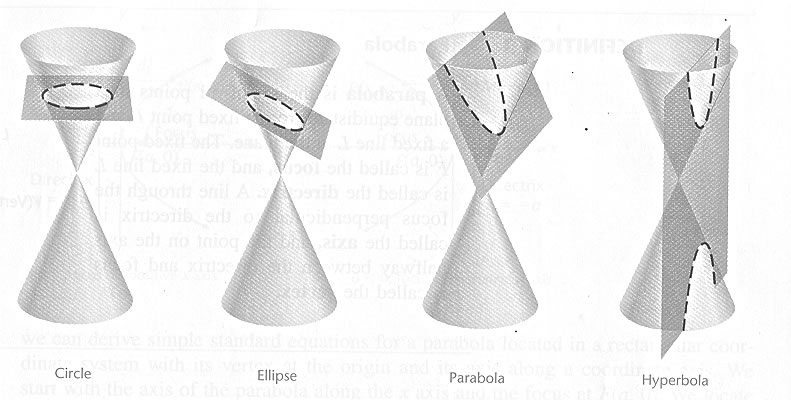
These graphs (curves) are called conic sections because they were originally defined
by ancient Greek geometers in terms of the various intersections of a plane
with the two nappes of a cone.
If a plane intersects one nappe, then
the curve defined by the intersection is a
circle
if the plane is perpendicular to the axis of the cone
ellipse
if the plane is not perpendicular to the axis of the cone
parabola;
if the plane intersects only one nappe but does not cut clear through the nappe
hyperbola
if the plane intersects both nappes but does not cut through the vertex
If the plane passes through the vertex of the cone, the resulting graph (curve)
a point
or
a line
or
a pair of lines
is
called
a
degenerate conic section
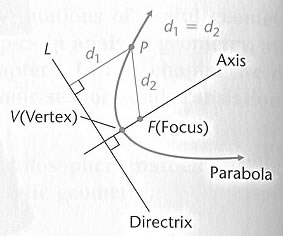
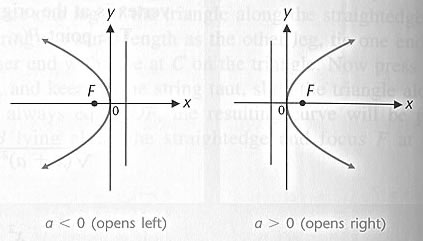
Coordinate-Free Definition of a Parabola
A parabola is the set of all points in a plane
equidistant from a fixed point F and a fixed line L
in the plane. The fixed point F is called the focus,
and the fixed line L is called the directrix
A line through the focus perpendicular to the directrix
is called the axis, and the point on the axis halfway
between the directrix and the focus is called the vertex
“
Using this definition of parabola within the context of a rectangular coordinate
system
we get the
Standard
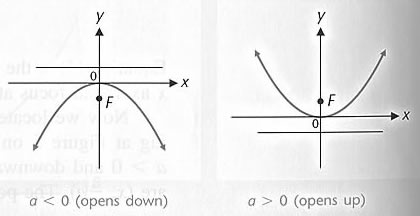
Equations of a Parabola with Vertex at (0,0)
1]
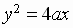
Vertex:
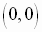
Focus:
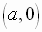
Directrix:
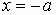
Symmetric
with respect
to
the x-axis
2]
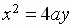
Vertex:
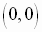
Focus:
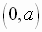
Directrix:

Symmetric
with respect
to
the y-axis
See Examples 1 – 2, pages 854 – 856,
of the textbook
Parabolic forms occur in nature
The trajectory of a thrown baseball
the paths in space of comets or meteors with certain amounts of energy
microphones
design of symphony halls
satellite antennae
shapes of lens in a flashlight
radar equipment
See Example 3, pages 857 – 858, of the textbook
top
next Ellipse



