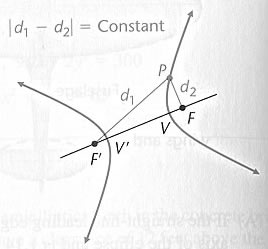
Coordinate-Free Definition of a Hyperbola
A hyperbola is the set of all points P in a plane
such that the absolute value of the difference of
the distances of P to two fixed points in the plane
is a positive constant
Each of the fixed points, F and F', is called a focus
The intersection points V and V' of the line through
the foci and the two branches of the hyperbola are
called vertices, and each is called a vertex
The line segment VV' is called the transverse axis
The midpoint of the transverse axis is called the center
of the hyperbola
Using this coordinate-free definition of a hyperbola,
we can derive the standard equations of a hyperbola
with respect to the x axis and y axis of a rectangular
coordinate system.
Standard Equations of a Hyperbola with Center at (0,0)
1]
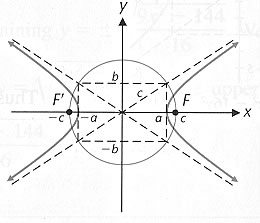
FIGURE 1
x intercepts:
y intercepts: none
Foci:
Transverse axis length =
Conjugate axis length =
2]
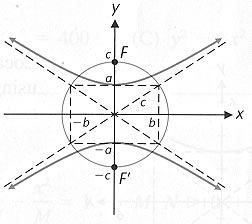
FIGURE 2
x intercepts: none
y intercepts:
Foci:
Transverse axis length =
Conjugate axis length =
Both graphs are symmetric with respect to the x axis, y axis, and origin
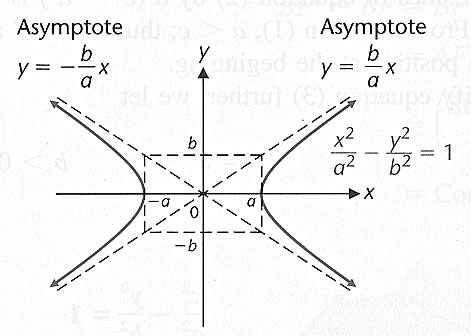
FIGURE 3
The lines
are the asymptotes of the hyperbola
The hyperbola approaches these lines as a point P(x,y) on the hyperbola
moves away from the origin
A quick way to draw these asymptotes is first to draw the rectangle shown in Figure 3,
then extend the diagonals of the rectangle
These extended diagonals coincide with the asymptotes of the hyperbola
The rectangle may be called the asymptote rectangle
The perpendicular bisector of the transverse axis, extending from one side of the asymptote rectangle
to the other side of the asymptote rectangle, is called the conjugate axis of the hyperbola
A circle, with center at the origin, that passes through all four corners of the asymptote rectangle
- see Figures 1 and 2 -
also passes through all foci of the hyperbolas with asymptotes determined by the diagonals of the rectangle
Hyperbolas of the form
and
are called conjugate hyperbolas.
They share the same asymptotes
See Examples 1 – 2, pages 876 – 878, of the textbook
Hyperbolic forms occur in nature
the orbits in space of meteors and comets having certain amounts of energy
loran radar systems
capillary action
nuclear cooling towers
optical instruments
top
next Translation of Axes