Systems
Involving Second Degree Equations
If a system of equations contains any equation that is not linear,
the system is called a nonlinear system
For example,
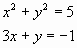
The solutions of such nonlinear systems may contain complex numbers, a+bi
We will assume that the replacement set for each variable is the set of complex
numbers,
which includes the set of real numbers
The process of solving a nonlinear system of equations may produce numbers
that do not satisfy all of the equations of the nonlinear system
Such numbers are called extraneous solutions, or extraneous
roots, of the system
It is important to check the derived solutions of any nonlinear system
in order to ensure that extraneous roots have not been introduced.
See Example 1, pages 690 - 691, of the textbook
Solution by Substitution
The substitution method used to solve linear system
may be used to solve nonlinear systems
See Examples 1 – 3, pages 690 – 693,
of the textbook
Other Solution Methods
Elimination –
see
Example 4, pages 694 – 695, of the textbook
Factoring and Substitution –
see
Example 5, pages 695 - 696, of the textbook
Graphic Approximation –
see
Example 6, page 696, of the textbook
top
next Matrices
Basic Operations
begin
Module 6
Matrices