Physics for the 2nd term: Kinematics

Part I: Concepts	Kinematics is the study of motion. Sa motion, several concepts ay ginagamit.
Scalar vs vector	Again, we go back to the very first lesson concerning scalar and vector quantities. The difference between the two is with the quantity they define. Ang pinaka-common na ginagamit na quantities in kinematics ay ang displacement, velocity at acceleration. Remember na velocity and displacement ay vector counterparts ng distance at speed. Vectors have direction, in addition to magnitude. Scalars have only magnitude. Sometimes, negative vectors do not necessarily mean negative magnitudes, pde rin going to the negative direction kaya nagka ganun.
Frame of reference	Frame of reference = the space in which an object is moving, na nakikita ng taong nakakakita. For example, may tao sa loob ng bus na naglalakad papuntang back of the bus habang bus ay nagm-move forward. From sum1 inside, ang tao ay makikita niyang going towards him (negative direction). Pero from sum1 outside, ang tao ay nagm-move forward kac d whole bus is moving forward.

Part II: Uniform Motion	This topic shows objects travelling at a constant speed. They experience zero acceleration, and the speed is the same all throughout the entire path. Preferred units ay m/s, km/h, mi/h
Formulas (formulae?)	Pinakaimportanteng formula dito ay speed = dist ÷ time. From this, pwdeng iderive ang dist. d = st And also time. t = d ÷ s
Problem Solving / Application	Compute the average speed of a formula one car in one race. On the average, ang isang race ay nagt-take ng 70 laps. In one lap, on the average, may mga 4.5km to complete a circuit. And on the average, a race lasts for about one hour and 45 minutes. Using these facts, maso-solve natin ang average speed ng mga f1 cars sa race. Solving for distance 4.5km/lap x 70 laps = 315km Converting time into hours 105mins ÷ 60mins/hour = 1.75hr Solving for average speed 315km ÷ 1.75hr = 180km/hr Therefore, ang average speed ng f1 race car ay 180 kilometres per hour. That's really fast. Check nyo rin ung units analysis. sa first one, nagcancel ung per lap nung i-mult. sa laps. Tapos sa next nagcancel nung dinivide ung 150mins sa 60mins. napunta sa taas ung hour kac dinivide. sa last naman no units cancelled so km/hr ung natira

Part II: Uniform Accelerated Motion	Shows objects travelling at constant acceleration. Their speed increases by the same amount every second. The unit of measure is any distance over the square of any time. Preferred unit ay m/s2
Formulas/e	velocity = acceleration x time     <--starting from rest vf = vo + at     <--in motion dist. = Vot + ˝at2     <--if starts from rest, then Vo = 0 and ur left w/ d = ˝at2 d = Vf2 - Vo2           2a
Problem Solving/Application	The main difference bet velocity and acceleration is dis: ang speed refers to how fast an object moves. gano kabilis siya nagch-change in position. While ang acceleration, refers 2 how fast an object changes speed, at what rate ba yun bumibilis or bumabagal. Using our previous problem sa formula 1, suppose nasa ibang circumstances, kung ang car ay nag- aaccelerate starting from rest and maintains a value of 6m/s2 until it reaches d average speed, gano katagal kaya ito naga-accelerate? Converting to m/s 180km/hr x 1hr/3600s x 1000m/km = 50m/s deriving time from 1st 4mula velocity = acceleration x time t = v ÷ a Solving for time t = 50m/s ÷ 6m/s2 = 8.3s Unit analysis: sa first nagcancel per hour sa hour, naging per sec. tapos cancel km sa conversion factor. Sa second nagderive lang. divided both side by acceleration to isolate time. Sa third medyo tricky. nag divide ka so ung s2 napunta sa taas. isang s ay nag cancel with the one below. may s na natira sa taas. then m divided by m ay nagcancel. Following the unit analysis mav-verify mo kung tama ung solution ehh. kaya importante din un. As it is, d f1 car takes 8.3 seconds to reach the average speed starting from rest.

Part II˝: Freefall	Special case of uniform accelerated motion. In freefall, an object is in motion without any xternal force acting upon it other than gravity. Always starts from rest, kac wla ngang initial force that acted on it.
Concepts/ Formulae (i prefer e)	Since the body is falling, we need to consider an object's acceleration due to gravity. Eto ay ang constant na -9.8m/s2 which replaces a in our UAM equations. This makes it easy kac one of the variables alam mo na. The formulae for speed and distance fallen are as follows:     v = gt    <--where g = -9.8m/s2     d = ˝ gt2    <--dito lam na natin ang g natin as opposed to normal UAM, value ng a varies Bakit negative lagi ung g? It's because of the effect of acceleration. If it moves to the positive direction (opposing gravity - UP) then the object is slowing down kaya naging negative. Pag speeding up naman (with gravity - DOWN) edi negative parin since it's going towards a negative direction. This comes in handy pagsolve ng equations minsan nagkakagulo dahil sa sign ng g. Hassle tlga ang g...
Problem solving/Application	A stone was dropped from the top of a cliff. If the speed at impact with the ground is 33m/s, how much time did it take to reach the ground and how high is the cliff? Derive time v = gt t = v ÷ g Solve for time t = 33m/s ÷ 9.8m/s2 = 3.37s Solve for distance fallen d = ˝(9.8m/s2·(3.37s)2) = 55.65m In 3.37 seconds the stone fell 55.65 metres. For the unit analysis, solving 4 time see previous example that shows dividing a velocity by an acceleration gives a time unit. sa 2nd magc-cancel ung per second-squared sa seconds-squared. ung ˝ wlang unit so un na un
Conclusion (for part II and II˝)	in uniform accelerated motion, velocity varies directly as time, and acceleration is the constant of variation. v = at2 means na pag mas mahaba ung time, pag mayroong acceleration, mas malaki ung final velocity. Sa freefall a is replaced with the constant g, which is equal to -9.8m/s2 distance naman varies directly as the square of time, with half of the acceleration as the constant of variation. if given an initial velocity before starting to accelerate, edi just get the speed change by mult. d acceleration by time. then add dun sa initial velocity na given. Freefall ay special case of UAM. laging zero ang initial velocity meaning it starts from rest. at ang acceleration ay laging constant (-9.8m/s2) kac eto ang acceleration ng falling body.

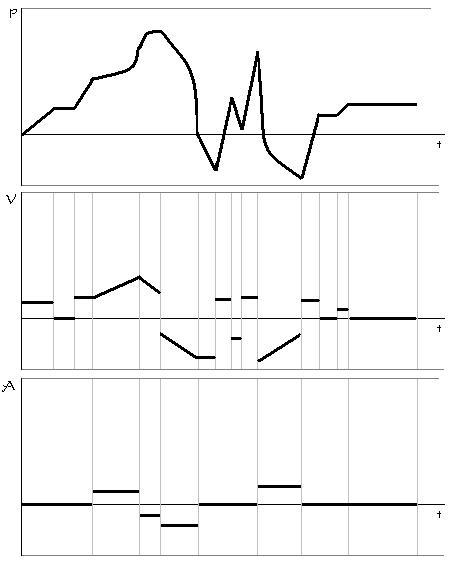
Part III: Motion Graphs	Madugong topic ito. Since this is a reviewer, dapat alam nyo na how to make rough kinematic graphs of the motion of the object, concerning the position, velocity and acceleration of the object.
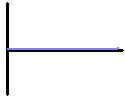
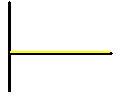
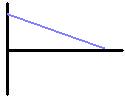
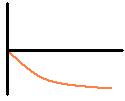
How to graph correctly/effectively	First thing to draw is the coordinate plane/matrix thingy. Magdraw ng L shape. In some cases, tho, ull have to extend the vertical line downwards. This gives room for negative values. The time is plotted on the x-axis (independent) and the y-axis can stand for displacement, velocity, or acceleration. Displacement-time graphs:   This usually starts from the origin (where the lines meet).   As the object moves, note of the direction its going, kc vector quantity ang displacement.   North, up, east and right give positive displacements. Draw above the x-axis (time line).   South, down, west and left give negative displacements. Draw below the time line.   Next, note the movement relative to the origin. It can be towards or away from it.   If away from origin, move farther upward or farther downward from the time line.   If towards origin, move from a point away from time line towards the time line.   An object at rest has a flat line.   An object moving at uniform motion has a diagonal line.   An object moving at uniform accelerated motion has a curved line.   Tandaan!: time is always passing, so you have to move to the right lagi. Can never move to the left   This also explains bakt ang x-axis puro nasa right lang. No such thing as negative time.   Slope of the graph gives the value for the velocity.   Changing slope means diagonal line for the velocity. Increasing steepness = increasing vel. Velocity-time graphs:   Sometimes this has a value at the beginning of time so it doesn't always start sa origin.   A zero value means the object is at rest   A flat line not at zero means the object is moving at constant velocity.   A diagonal line means the object is accelerating - there is a change in velocity.   Wlang curved line sa v-t graph. At least, wla dito sa zobel/highschool.   A negative velocity means a negative direction, not a negative magnitude.   Slope of the line becomes the value for acceleration. If constant velocity, zero accel.   Area between the line and origin becomes the position/displacement. Acceleration-time graphs:   Wlang slanted lines dito, since wlang curved lines sa v-t graph. Lahat flat lines.   At zero can either mean at rest or moving at constant speed.   Only pag may change in velocity magkakaroon ng value. And it's always a flat line (highskul)   Negative acceleration can mean a positive magnitude but a negative direction or..   A negative magnitude. Pag negative magnitude it means object is slowing down.   Area bet. the line and the origin becomes the value for velocity.
Examples of graphs	# Position-time Velocity-time Acceleration-time 0 1 2 3 4 5 6 7 8 9 10 11 12 Pagpasensyahan na sobrang daming pics.. ang hirap tuloy i-load lahat ng pics. Pag di lumabas baka nagt-timeout ung pagload ng pics, just right click kung san dapat may pic and press "show picture".
Motion story	The complex version of the graphs. Dito ic-combine several cases of the graph. Gagamitin ko nalang para dito ang project namin ni ryan sa science. Along Acacia Avenue in Ayala Alabang, a man was walking with constant velocity. After a while, he stopped and checked a nearby parked car. He had an evil scheme so he stole the parked vehicle. A patrolling officer saw him and started to shoot at him but the man was quick enough to hot-wire the car and drove off with haste. The officer followed him around the village with changing speed and directions at several times. After a while, the car went out of control and hit a tree. The man tried to run but he got surprised by a hiding officer. The officer quickly shot him and he lay on the ground with a bullet in the head. the most impt. thing to remember ay ang pag-split ng position graph into unique time intervals. this way you can create the v-t and a-t graphs step by step.

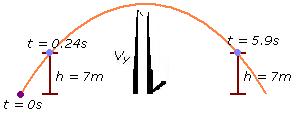
Part IV: Projectile Motion	Coming soon! just in case di umabot, pls study!!!
The concept	Motion of an object projected in a gravitational field. The object thrown, called the projectile, then follows a curved path (called its trajectory). The paths of these projectiles vary on what initial velocity it was projected with, the angle of inclination, and the object's height from the ground. We will apply many of the lessons that were tackled this year sa physics, these include resolving vector quantities to x and y components as well as the lessons in UM and UAM. Actually projectiles ay combination ng UM and freefall. There are just special cases involved w/c add a few extra steps to the problem solving
Formulae	A certain V is given, to resolve it in its x and y components use trigonometry: initial velocity is written as Vo kasi un ang velocity at 0 seconds (the start) x-component: Vx = Vocos θ y-component: Vy = Vosin θ Sa x portion ng projectile travel ay nagf-follow ng uniform, non-accelerated motion. For the whole horizontal part ay constant ang speed. We are concerned with the object's speed and the horizontal distance it travelled (referred to as Range) range: R = Vxt (simply like solving for a distance which is speed x time) velocity-x: Vx = R                            t Derived it from the above equation, not likely to be used since u can use the Vx = V ocos θ Sa y component is a different matter. It makes use of UAM, ung constant na acceleration nito ay dahil sa gravity (at a constant -9.8m/s2). If it is projected upwards at an angle, it slows down going up (see thinning arrow) and speeds up going down (arrow is getting fatter). Pag horizontal lang ung projection, wlang initial y-component pero it increases w/ time kac may acceleration nga. Using the y-component also gives us the time of flight, the only value linking both the x and the y components of the velocity. Solving for final velocity: [ Vf = Vo + gt ] This shows that the final vel. is equal to the initial plus how much it accelerated for the time it was travelling Solving for the vertical dist. travelled: [ dy = Vot + ˝gt2 ] Parang ung uniform accelerated motion. Pag wlang Vo then: [ h = ˝gt2 ] This is the height na for projectiles. If it's the special case (diagram 1) edi ung height neto ay just a one way trip, it doesn't include na the distance it travelled pababa. Diagram 2 wlang prob. since the height is just the distance it fell. [ t = 2Voy ÷ g ] deriving time from the first equation [ Vf = Vo + at ] you get the equation above. This is helpful lalo na sa special case (diagram 1) kung san given sayo ang Vo pero walang height. Nagkaroon ng 2 dun dahil kung wla, that's just the time going up (at the top, Vfy is equal to zero, kaya nawala na ung Vf completely). Double it to get d total time of flight. [ t = √2h ÷ √g ] or [ t = √(2h ÷ g) ] basta sq.root ng buo eto naman helpful for those under diagram 2. Usually kac given na ang height na binagsak tapos u need 2 find all components. Dinerive to mula sa 3rd equation [ y = ˝at2 ] na merong square of time.
Problem solving	Instead of the normal ako gagawa lahat tas nakadrawing lang, ssbihin ko nalang ung formula dat u need to use, with some hints. Question Formula/e Hints/Notes Object is dropped from top of a place and hits the ground after t time. How high did it fall h = ˝gt2 freefall lang ito What was the velocity upon hitting ground Vf = Vo + gt Vo = 0 Object is thrown directly downward with speed of Vo. How fast will it be going at t time Vf = Vo + gt parang UAM pero a = g How far has it fallen after t time d = Vot + ˝gt2 and g = -9.8m/s2 Object thrown vertically into the air with speed Vo How high does it go tup = -Voy ÷ g Voy = Vo since θ = 90 d = Votup + ˝atup2 right part becomes minus kac -9.8 How long before it returns 2 ground t = 2tup Going up same as going down so x2 Object thrown horizontally from top of h height structure. It lands R range away from structure. How long b4 reaching ground t = √(2h ÷ g) di pa gagamitin range What was the Vo on x direction Vox = R ÷ t yan, nagamit din pala ung formula Ano ung velocity when it hit d ground Vf = Voy + at Voy = 0 Guy jumps at an θ and at Vo initial What was his Voy Voy = Vosin θ pag wlang x or y sa given, i-resolve How long does s/he stay in air t = -2Voy ÷ g total kac pag pababa, still in air How far does s/he reach horizontally R = Voxt resolve. use R = Vo(cos θ)t How high does s/he reach h = ˝gt2 neglect negative sign
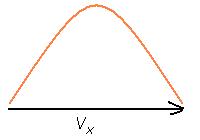
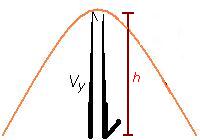
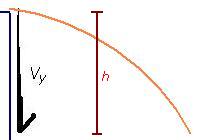
Rules to remember:	There is no x velocity if the launch angle is 90°. There is no y velocity if the launch angle is 0°. If there is no y velocity there is no flight; wlang mgyyare if 0° ung angle, kahit gano kalakas i- launch. Increasing the launch angle increases the time of flight; max time if 90° ang launch θ. The projectile has maximum range at θ = 45°. Also, the x and y velocities are equal. Any launch angle below or above 45° will give a shorter range. Complimentary angles (add up to 90°) have equal ranges but different times of flight. The perfect curve (equal height and range) occurs at θ = 76°. Changing the Vx will not affect time of flight Changing the Vy affects the time of flight and subsequently, the range.
Harder problems	Dito titignan ang quadratic formula, pati na rin ung pagc-combine ng mga equations in one. Quadratic A cannonball is launched at 35m/s at an angle of 60°. What time will it be at 7m above the ground? Note We will be using first the [ d = Vot + ˝at2 ] and in math, the quadratic formula. Tandaan na ang quadratic formula ay [ x = -b ± √(b2 -4ac) ÷ 2a ] y-component Voy = 35m/s(sin 60°) This is mga 30.3m/s Derive formula [ d = Vot + ˝at2 ] Plug in the known values first 7m = 30m/s(t) + (-4.9m/s2)t2 Move to left side to get At2 + Bt + C = 0 4.9t2 - 30t + 7 = 0 Now use the quadratic formula to get values of t Solution t = -b ± √(b2 - 4ac) ÷ 2a yung x naging t kasi un ung quadratic var. substitute 30±√[(-30)2-4(4.9)(7)]÷2(4.9) ang dami!hehe. use coefficients of terms sa letters = (30.3 ± 27.9) ÷ 9.8 resolved the [ ] tapos compute this answer 2.4 ÷ 9.8   and   58.2 ÷ 9.8 we get two answers for t Answers 0.24 seconds This is the time while going up 5.9 seconds This is the time coming back down Makes sense since pag project, on its ascent, 0.24 seconds palang nagpass ay umabot na sa 7m ung height from ground. Tapos some time passes, during this time tumataas until mareach ang max. height then starts to come back down. At 5.4 seconds after pinroject ay 7m nalang ang height from the ground. Combination An archer aims at a target 218.95m away. Assuming he cannot see the target directly and he has to shoot upwards, what is the minimum and the maximum angle he should fire with para mahit ung target if he shoots at 47m/s? Analysis Given na ang range and our initial velocity (not split into components). We are looking for the two angles that will give us the range. From the discussion alam na natin that these two angles are complimentary. Pwedeng isang angle nalang ang icompute natin and subtract it from 90° to get the other. We can also substitute other formulae into a main formula para isang solve nalang ang gagawin. Formulae needed R = Voxt The main equation, dito ip-plug in ung other equations Vox = Vocos θ Use in place of Vox in the above equation t = 2Voy ÷ g Use in place of t sa first equation Voy = Vosin θ Use in place of Voy in above Master formula R = Vocos θ (2Vosin θ)                   g Plugged in na lahat Derive the closest to θ Rg = Vocos θ2Vosin θ Divide both side by 2 and Vo2 kac dalwa ung Vo sa right    Rg    = cos θsin θ  2Vo2 Nakuha ko na ung identity! [ cos θsin θ = sin 2θ ]                                                                          2    Rg    = sin 2θ  2Vo2         2 Note: di yan 2sin θ ..un angle na makuha mo sa sin-1, half lng nun ung sagot. Solve 218.95(9.8) = sin 2θ       2(472)            2 mult. both side by 2 para maiwan ung sin 2θ 218.95(9.8) = sin 2θ        472 (nagcancel ung dalwang 2 sa left) 0.97 = sin 2θ use Arcsin/sin-1 (shift+sin sa calcu) 76° = 2θ divide this angle by 2 to get the minimum launch angle θ = 38° eto na ung minimum angle! subtract from 90 to get the max The Angles θ = 38° The first one (lower angle, shorter time of flight) φ = 52° From φ = 90° - θ (higher angle, longer time of flight) Phew! sa wakas nakuha ko na.. umm, it's kinda late though hahaha.. salamat pala sa lahat ng nag-contribute ng kanilang "intellectual property" d2 pati sa ibang subjects. consider urselves part of d copyright narin! hahahaha. 108 \m/

© 2004 by Luis Medina. Unauthorized duplication and distribution of this document will be persecuted and is punishable by federal law.... ayus!