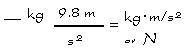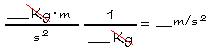| Part I: Setting up Equations |
|
| Summary:
Ito yung talagang kailangan malaman for the next parts. Ita-tackle narin dito ang units of measure,
conversion at factor label method. |
|
| First topic:
Units of Measure |
Usually in the items in the first term exam, 3 units lang ang gagamitin sa lahat ng problems.
The quantities we usually measure can be expressed in variations of these units. The three are
Kg, m, and s. We combine these units to get acceleration, force, weight, work done, distance at kung
anu-anong pinahanap sa atin. |
Conversion is easy. Just memorize the Tera-Giga-Mega ek-ek Happy Bday song. This applies to all
metric quantities.
Tera-Giga-Mega-Kilo-Hekto-Deka-(unit)-Deci-Centi-Milli-Micro-Nano-Pico [in descending order] |
In other conversions naman, let's hope madadali yung ilagay sa test. Sana the things we know.
1ft = 12in
1in = 2.54cm
1kg = 2.2lbs
*mga ganyan, un mga madadali lang sana. |
| Second topic:
Factor-label method |
Siguro iniisip nyo "ano un? watdapak?" Pero sa totoo, ung factor-label method ay madali lang, ito
ay isang way to illustrate how you got certain units in the process of computing for the final
answer. |
| |
Basically, the rule you need to remember is when you encounter same unit in the same part of the
equation (numerator pareho/denominator pareho), mas-square ung unit. And when they are on opposite
parts ay magc-cancel silang dalawa. It's also really useful kung alam mo what unit you're supposed
to get, tapos mali ung nakuha mo, it tells you na mali yung computation mo. With the calculator,
wala na nagco-compute manually, pero i suggest writing it in FLM para malaman mo na tama ang dapat
pindutin. |
| Example 1: |
Compute for weight (unit: Newton) by multiplying mass by acceleration of gravity.
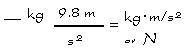 |
|
As you can see, walang nag-cancel, nacombine lahat. Note that the unit for Newton(N) can also
be expressed as kg·m/s2 |
|
| Example 2: |
Compute for acceleration of gravity, given mass and weight.
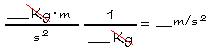 |
|
Here, nag-cancel na yung Kilograms. You're left with m/s2 |
|
| Part II: Vector Quantities |
This section tackles Vectors, adding vectors and the graphic and component methods. |
| Summary:
Vector quantities differ from scalar quantities in that they have both magnitude and direction,
whereas scalar quantities have only magnitude. Where scalars have only 1 dimension, vectors have two.
|
Examples of vectors are velocity and acceleration. The scalar counterpart
is speed. Another example of a vector quantity is force. Scalar counterpart
is energy. |
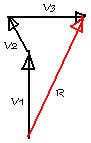
| Adding vectors: graphical method |
Two basic methods: head-to-tail and tail-to-tail.
| Head to tail: |
Tail to tail: |
|
 |
 |
In adding vectors, our objective is to get the resultant vector, this vector is the sum of all
the magnitudes of the vectors. Parang treating all the vectors as one. |
| Put the tail of the next vector on the end of the preceeding vector. Then, connect the tail of
the first to the head of the last. That is your resultant vector. |
Draw a line from the end of one vector. This line should be parallel to the other vector. Then
connect the intersection of their tails to the intersection point of the two parallel lines. |
Note that the tail to tail method can be used only for two vectors. |
|
| Adding vectors: component method |
Treat vectors as the components of the resultant vector.
| First, split all the vectors into the x and y components of each one, then add all
the components, and then get the resultant of the total x and y components. |
Add these vectors:
1] 14m, N
2] 22m, 67° south of west
3] 6.97m, 15° north of east
4] 3.28m, NW
|
Component method makes use of the three fundamental principles in
finding the sides of a right triangle, or in trigonometry, SOHCAHTOA (salamat ms munar!) (ms
paclarin pa pla). |
| The easiest way is to tabulate your data. Mamaya, i-explain ko how we know what trig function
to use. |
| Vector |
x |
x comp |
y |
y comp |
| 1 |
14m(cos 90°) |
±0 |
14m(sin 90°) |
+14m |
| 2 |
22m(cos 67°) |
-8.6m |
22m(sin 67°) |
-20m |
| 3 |
6.97m(cos 15°) |
+6.7m |
6.97m(sin 15°) |
+1.8m |
| 4 |
3.28m(cos 45°) |
-2.32m |
3.28m(cos 45°) |
+2.32m |
| Resultant |
(Add all x's) |
-4.22m |
(Add all y's) |
-1.88m |
|
| To get the resultant of the two components, use tangent. |
tan θ = | y ÷ x |
= | -1.88m ÷ -4.22m |
= 0.45 |
[ibig sabihin, tangent of the angle is equal to the absolute value ng
y-component over x-component] |
| *Get the angle which has a tangent of 0.45, use tan-1 |
Arctan 0.45
= 24° |
Using the signs (+ or -) of both components (x and y) of the resultant, malalaman nadin natin
ang direction ng vector. In this case, since both are negative, quadrant III tayo, then it's goin
24° south of west. |
| *Use any component and the computed angle to get the magnitude. neglect signs |
cos θ = adj ÷ hyp
hyp = adj ÷ cos θ |
so use the x-component to get the value of the resultant vector.
R = 4.22 ÷ cos 24°
= 4.62m |
| *Can also be computed using the other component and the other trig function. neglect signs |
sin θ = opp ÷ hyp
hyp = opp ÷ sin θ |
using the y-component this time, and the sin function, we get the same answer:
R = 1.88 ÷ sin 24°
= 4.62m |
| *Can also be computed using pythagorean theorem. |
Pythagorean theorem:
c2 = a2 + b2 or
r = √(x2 + y2) |
c = √ (-4.222m + -1.882m)
= √21.34m
= 4.62m |
| We will use application of the component method in all succeeding lessons. |
|
| Explanation: |
 |
|
R is our vector, Vx and Vy are the components. Ax is congruent to Vx and Ay is congruent to Vy.
θ is the angle. In this case, R is a vector with direction to the southeast. Using SOHCAHTOA
we find that to get Ay we use [ sin θ = Ay ÷ R ] and derive from there. That will also be the
length of Vy since they are congruent. Using the other triangle, we can use cos and the value of
[ 90 - θ ] |
|
| Part III: Normal Force |
|
| Summary:
Normal force refers to the force that supports an object currently in equilibrium on a certain
plane. It is always perpendicular to the horizontal plane that the object being acted upon is
resting on. |
| Formula:
Fn = w(cos θ) |
*ang theta (θ) refers to the angle of the plane. If plane is flat on the
ground, then θ = 0 and (cos θ) = 1 |
| Special Cases:
If the plane is inclined, then you use the normal formula. But if the plane is flat, for example
the ground itself, then you do not need to do the cos part of the equation, since we know that
cos of 0° is 1. |
*naging 0° yun angle since walang elevation or incline from the ground. |
| How to solve problems involving normal force. |
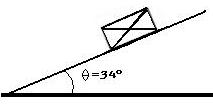
| Problem 1:
Compute for the normal force in the diagram to the right if the mass of the object is 7.5kg. |
 |
Step 1:
Find the weight of the object. Dahil nadiscuss na in previous lessons that weight is equal to the
mass of the object times its acceleration due to gravity, magagamit na natin ang equation na ito.
Formula: w = mg
*we also know the constant of acceleration due to gravity.
g = 9.8m/s2 |
|
w = mg
= 7.5kg(9.8m/s2)
= 73.5kg·m/s2
= 74N |
*the formula from step1.
*substituting the values
*the answer and units
*following correct significant figures and Newton(N) = kg·m/s2
|
|
| Step 2:
Indicate the given and use the free body diagram. Usually hassle gawin to pero sabi ni sir na if you
have the given and the free body diagram in your solution, marami kang makukuhang points na pangbawi
in case your solution is wrong. And it also helps you para di ka maconfuse sa gagawin. |
|
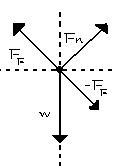
Given:
w = 74N
θ = 34º
Fn = ?
|
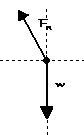 |
*In the Free-Body Diagram (FBD), we need to show only the forces that
are currently acting on the object. Label them also. In stating the given, you need to include
the quantity we are looking for. Lagyan nyo nalang ng ' ? ' |
|
| Step 3:
Solve for the Normal Force using the given formula. |
|
Fn = w (cos θ)
= 74N (cos 34º)
= 74N (0.83)
= 61.35N
= 61N |
*eto ung given formula
*substituting the known values
*solved (cos 34º)
*computed answer
*correct significant figures, no units to be changed, final answer na |
|
| *Enough na siguro ang one example. In fact, this should cover the
lesson on normal force na, because in the example I gave, meron ng angle, and the values aren't
that exact. Tandaan lang na pag flat sa ground yung object, you don't need to get the angle.
θ = 0º and cos 0º = 1. Therefore, normal force is equal to the weight of the object, or Fn = w.
Easy, no? Ngayon, ie-explain ko pano nakuha ung formula na Fn = W(cos θ)
|
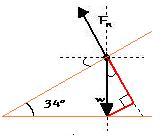
Baket naging ganun ung formula?
Since alam natin na ang normal force ay ang amt of weight of the object that is being supported by
the plane, and that it's perpendicular to the horizontal plane itself, and since na-establish ni sir
ezrel and ms panaligan that "the summation of forces acting on a body is equal to zero", madali ng
ma-explain ang formula of normal force using some knowledge of trigonometry (tnx to ms munar and ms
paclarin) |
 |
|
If we use the previous example, makikita natin na we form a right triangle if we
extend the lines. The orange lines are the inclined plane that the object is resting on. The red
lines are the sides of the right triangle that we form. The three angles you see (ung tatlong me
arc) are all congruent. They are all equal to your θ which is 34º. Since ang normal force
ay always perpendicular to the plane, by extending it we can get one side of the triangle. From
the tip of the weight vector, draw a line parallel to the plane, and you have the last side of
the right triangle. Ngayon, pano natin makukuha ung side na un? Tinuro sa atin last yr ang rule
of SOHCAHTOA when dealin with right triangles. In this set-up we will use the CAH part of the
rule. Since
cos θ = adjacent/hypotenuse ; then
adjacent = hypotenuse (cos θ)
Pag tinignan yung diagram sa left, we can see that our θ is at the top, so to find the
adjacent side we multiply the hypotenuse (which is our w), with the cosine of the angle. This
adjacent side is now equal to our Normal Force. |
*Sa test we don't have to prove the equations (hopefully), nilagay ko lang ito for
those who wonder bakit naging ganun yung equation. Para they know all sides of d story..
*sorry kung ang labo nun pic, ginawa ko sa paint and when i compressed the file, it lost so much
quality. |
|
| Part IV: Force of Friction |
|
| Summary:
The force of friction refers to the force that maintains a body's state of equilibrium. It allows the
object to remain at rest using contact with a surface. The Force of Friction is equal to the normal
force multiplied by a certain coefficient w/c varies from surface to surface. It is also known as the
equivalent amount of opposite force required to push the object into a state of motion. |
| Formula:
FF = µFn |
*ang µ ay ang coefficient of friction (this depends on your surface) |
| Special Cases:
In these sets of problems, bibigyan tayo ng iba-ibang quantities that we must solve for. Pwedeng mass
yung hinahanap, pde rin coefficient of friction. Analyze the problem and find out what you're going
to solve for. Then solve it. |
*some knowledge of derivation of formulas will help. Para iro-rotate nyo nalang yung formula
to isolate the needed variable using transposition. |
| How to solve problems involving force of friction. |
| Problem 1: What is the mass of an object which takes 43N of
energy to move on the floor with a coefficient of friction equal to 0.37? |
Analyze the problem:
Para mong sinabe kelagn mo ng 43N of energy to move an object on a surface which has a coefficient of
friction of 0.35
De joke, inulit ko lang ahahaha.. |
| Step 1:
State the given and unknown quantities and sketch the free body diagram. |
|
Given:
m = ?
FF = 43N
µ = 0.35
Fn = ?
w = ?
|
 |
Complete formula list for Force of Friction:
FF = µFn
µ = FF/Fn
Fn = FF/µ
Master formula for this problem:
|
| *it seems as if sobrang daming unknown, pero kaya yan, because all these are
related to one another and madali lang yan if you work in the correct order. Also, mass is
indented kase un yung final answer that you are looking for. |
|
| Step 2:
Analyze the problem and solve for the first unknown given the above formulae: |
|
Fn = FF/µ
= 43N/0.35
= 122.9N
= 120N |
*given formula
*substitute known values
*computed answer
*significant figures |
*since the angle of elevation is Oº, we do not need to compute the weight of the object anymore.
Naka-flat na sya sa ground so all we need to do is to equate normal force to weight. That will
give us the weight. (see previous lesson on normal force)
w = Fn
w = 120N
|
|
| Step 3:
Find the mass of the object given the weight. Use the formula w = mg and from it derive the
equation m = w/g. |
|
m = w/g
= 120N / (9.8m/s2)
= 12kg |
*formula
*substitute known values
*computed and final answer |
*this is the last step. since we are looking for the mass, pabaliktad tayo magwo-work. Given na
yung force of friction but we need to find the mass (usually kase, mass ung given quantity.) also
notice na ang unit ng mass ay kg. natira ang kg after dividing Newtons by m/s2. since
ang Newtons ay kg·m/s2, its logical na kg nalang ang natira. |
|
| Note:
We can also use the master formula given sa me taas (ung picture na m = FF/µg |
|
m = FF/µg
= 43N / 0.35(9.8m/s2)
= 43N / 3.43m/s2
= 12kg |
*notice we get the same answer. derederetso na un computation. by substituting the
other known formulae, i came up with a single formula para 1 calcu use nalang. minsan kac mahirap
pag napindot mo pala AC dun sa calcu, u have to compute again. anyway, gawin nyo lang to if you
really know what your doing kac nakakalito siya, but it saves you time(parang UPCAT ang naging
dating ah). |
|
|
|
| Problem 2:
Refer to the diagram and compute for the Force of Friction. The coefficient of friction is 0.18 |
|
 |
*Kumpleto itong problem na ito. It's straightforward lang so it's easy. You're given
the initial quantities (mass, µ, and θ). Use the formulae in order, to get to the final answer
which is your FF. |
|
| Step 1:
As usual, identify the given and draw the free-body diagram. |
| |
 |
Given:
m = 16.6Kg
w = ?
θ = 27º
µ = 0.18
Fn = ?
FF = ? |
Recall:
w = mg
Fn = w·cos θ
FF = µFn |
|
| Step 2:
Solve. |
| |
w = mg
= 16.6Kg(9.8m/s2)
= 162.68Kg·m/s2
= 163N |
Fn = w·cos θ
= 163N(cos 27º)
= 145N
|
FF = µFn
= 0.18(145N)
= 26.1N << Final |
|
| *Note that µ cannot be greater than 1. Hindi pde un or else sobrang hirap naman nun if
you want to make an object move you'll have to apply force equal to its weight. Note also that you
have to express the answer in correct significant figures (although sir ezrel is not strict about it,
just to be sure gawin nyo parin) and in correct unit of measure (eto kelangan sundin talaga). |
| Part V: Translational Equilibrium |
|
| Summary:
Translational Equilibrium is a state of an object in rest. This equilibrium is different from the
other in that all the forces acting on the object meet at a certain point. A good example of this
situation is in an object being held in rest by a rope, cord or string. The force we compute for is
the tension of the cord. |
in other words, may isang point na lahat ng forces meet. this is the center of mass of the object.
mas madali to kesa dun sa rotational because the origin of the coordinate plane in the FBD is the
center of mass of the body. usually, ang ipapahanap sayo ay ang force of tension. analyze the
questions well and you can answer them with ease. mahirap lang tlga mag-analyze. |
| Formulae:
madami dito, refer to the complete list to the right. |
General Formulae:
ΣFX = 0
ΣFY = 0 |
 |
|
Trigonometric Formulae:
VY = VRsin θ
VX = VRcos θ
|
| *Σ means summation, or means adding all the quantities of that type. |
in adding these, take into account all the vectors to that axis. also, remember to use proper
signs. downward force is a negative vector, so is a force going to the left. |
The trigonometric formulae came from the SOHCAHTOA rule.
VY came from SOH and VX came from CAH. |
|
| Special Cases:
Many to mention, refer to the problem solving part. |
*feedback nyo pakilagay nlg sa yahoogroup (if you'd want this one for other subjs as well, if you
think it should be condensed further, if you like d layout, etc.) |
| How to solve problems involving translational equilibrium. |
| Problem 1:
The figure on the right shows a weight being held in equilibrium by two ropes. Find the tension in
each of the ropes. |
| |
 |
|
*In this diagram 3 values are given: the weight of the object, and the values of the
2 angles of depression from the horizontal. You have to set-up the equation using the general
formulae, the SOHCAHTOA rule and other trig knowledge. |
Layout by |meDz| |
|
| Step 1:
Draw the free-body diagram. |
| |
 |
|
*Bakt napunta sa baba ung dalwang angle? Eh diba nasa taas dapat un?? |
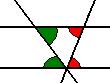 |
*We learned last school yr in Trigonometry that when two parallel lines are cut by
another line which intersects both (called a transversal) then congruent ang alternate
interior angles. The diagram clearly shows this. Like colors mean congruence. |
| Actually sinabe na yan dati pa na pareho lng ung 2 angles. I just explained it para
lam nyo bakit. |
|
| Step 2:
Set-up your solution by finding the equation for all variables. |
| |
ΣFX = 0
TBX + TAX = 0
ΣFX = 0
TBY + TAY - w = 0 |
X-components
TAX = -TAcos θ
TBX = TBcos Φ |
Y-components
TAY = TAsin θ
TBY = TBsin Φ |
|
| Step 3:
Derive variables using cominations of substitution and transposition. |
| |
TAX + TBX = 0
-TAcos θ +TBcos Φ = 0
TBcos Φ = TAcos θ
TB = TAcos θ
cos Φ
TB = TAcos 67°
cos 43°
TB = 0.53TA |
*From ΣFX = 0
*Transpose TAcos θ
*Divide both sides by cos Φ
*Substitute known values (angles)
*Divide
*Derived formula for TB |
|
| Step 4:
Solve for the remaining variables. |
| |
TAY + TBY - w = 0
TAsin θ + TBsin Φ - w = 0
TAsin θ + 0.53TA sin Φ - 74N = 0
TAsin θ + 0.53TA sin Φ = 74N
TA(sin 67° + 0.53sin 43°) = 74N
1.28TA = 74N
TA = 57.72N |
*From ΣFY = 0
*Substitute answer from Step 3 for TB
*Transpose 74N
*Factor out TA and resolve parenthesis
*Divide both sides by 1.28
*Tension of Rope A |
*Use formula from Step 3 to find TB
TB = 0.53TA
= 0.53(57.72N)
= 30.59N |
|
| Part VI: Rotational Equilibrium |
|
| Summary: State of an object wherein it tends to rotate, because the forces that
are acting on the object do not meet at one common point. Because of this, the object tends to
rotate. The resulting quantity from the product of the force applied and the length of the moment arm
is known as Torque. |
| |
Example: |
 |
|
*Tendency of the body is to rotate. |
If the object is in equilibrium, then the summation of torques is equal to zero. It
is given by the equation:
Στ = 0 |
|
| Formula: τ = FL where τ is your torque. |
*Torque only considers the force applied perpendicular to the moment arm. |
| Special Cases: Depends on the given problem. |
| *Things to remember when dealing with Rotational Equilibrium. |
| |
*Forces which tend to rotate the object counterclockwise have a positive torque.
*Forces which tend to rotate the object clockwise have a negative torque. |
*Di ko na ilalagay yung "right hand rule". The only things you really need to keep in
mind are [counter = +] and [clock = -] |
Units- Name (symbol): unit
Moment arm (L): m
Force (F): N
Torque (τ): N·m |
|
| How to solve problems involving Rotational Equilibrium. |
| Problem 1:
Find the torque of the force applied to the wrench. θ = 60° |
| |
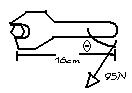 |
*Analyze:
You need only the force perpendicular to the moment arm. When you have this, you can
solve directly for the torque. |
Given:
L = 0.16m
F = 94N
F| = ?
θ = 60° |
|
| Step 1: Find the force perpendicular to the moment arm. In this case it is the
y-component of the given force applied. Then solve for the torque using the given formula. |
| |
Since the force makes a 60° angle with the moment arm, and you need a 90° angle (to
make it perpendicular), then our new θ is 30°. Find the y-component using SOHCAHTOA. |
|
95N(cos 30°)
= 82.3N |
τ = F|L
= 82.3N(0.16m)
= 13.2N·m |
|
| *Practical application: see-saw |
| Problem 2:
A boy, weighing 50kg, sits on one end of the see-saw. His brother, weighing 64kg, sits on the other
end. The see-saw is 4 meters long. How far from the center must their sister, weighing 40kg, sit so
that the see-saw will be perfectly balanced? |
| |
 |
*Note that the see-saw is balanced at the middle (meron ba namang see-saw na hindi
nakagitna? meron cguro, pero we assume nakagitna to). In effect, the two opposing forces are set
equidistant from the center. We also assume that the sister will sit somewhere on the left side.
Explain ko in step 1. |
|
| Step 1: Set-up the equation. It's easy if you use a table to organize the many
values you have to solve. Mas organized kase. |
| |
| Force |
Mass (Force) |
Distance |
Torque |
Sign |
| a |
50kg(9.8m/s)
= 490N |
2m |
490N(2m)
= 980N·m |
Counter (+) |
| b |
64kg(9.8m/s)
= 627N |
2m |
627N(2m)
= 1254N·m |
Clockwise (-) |
| c |
40kg(9.8m/s)
= 392N |
? |
392N·L |
Counter (+) |
|
|
*Bakit inassume na force c(the sister) is sitting on the left side (resulting in a +
sign since she will rotate the seesaw counter-clockwise)? Syempre, if we will use common sense, we
see na mas mabigat ung 64kg kesa sa 50kg, and they are equidistant from the center. So alanganaman
tumuntong pa cya sa mas mabigat na side eh we wish to balance the seesaw nga eh. |
|
| Step 2: Solve for the missing length. |
| |
Στ = 0
τa - τb + τc = 0
980N·m - 1254N·m + 392N(Lc) = 0
-274N·m + 392N(Lc) = 0
392N(Lc) = 274N·m
Lc = 0.699m
|
*General Formula
*Substitute respective torques w/ proper sign
*Substitute known values, solving for Lc
*Transpose -274N·m
*Divide both side by 392N
*Final answer
|
|
| The sister must sit 0.70m or 70cm from the left side of the center. |
|