
Figura 1. Cargas eléctricas a lo largo del eje x
Medardo Fonseca
Universidad Distrital
E-mail : mefle@yahoo.com
Publicado en la revista FÍSICA
Y DIDÁCTICA, Universidad Distrital. Vol 1. No 1. (1999).
Resumen
Cuando se trabaja en el campo de la electrostática, normalmente hay que recurrir a la imaginación para hacerse a una idea de como es el campo y el potencial eléctrico generado por una serie de cargas eléctricas. Afortunadamente la tecnología informática provee herramientas que contribuyen a la enseñanza y a la comprensión de los conceptos físicos; con la ayuda de un programa de computador vamos a visualizar algunas situaciones particulares.
Introducción
En la enseñanza secundaria y en los primeros semestres de la universidad nos encontramos con un tema bastante abstracto e intangible como son las cargas eléctricas, sabemos que estas generan campos eléctricos y que estos afectan a otras cargas eléctricas. En general podemos afirmar que la región del espacio donde una carga eléctrica experimenta fuerzas eléctricas se denomina Campo Eléctrico1. El Campo eléctrico es un campo vectorial y por tanto hay que tener cuidado al hacer cálculos y no olvidar que los vectores son orientados.
Afortunadamente hay herramientas informáticas que permiten hacer cálculos numéricos, simbólicos y visualizar gráficamente fuerzas, campos y potenciales eléctricos. Estas son las herramientas CAS (Computer algebra systems) y Mathcad es una de ellas2,3. A continuación vamos a desarrollar unos ejemplos muy sencillos con la ayuda de este programa.
Ejemplo 1: Dibujar el campo eléctrico a lo largo de la línea que une dos cargas eléctricas.
Solución: supongamos que las cargas están en la posición (1,0) y (8,0) metros

Figura 1. Cargas eléctricas a lo largo del eje x
Se escriben las constantes, las cargas, el rango de x, la ecuación del Campo eléctrico para hacer luego la gráfica.


Figura 2. Programa E_2cargas.mcd para visualizar el campo eléctrico generado por dos cargas eléctricas
Como se puede apreciar en la figura 2 hay claramente tres regiones: en la primera a la izquierda que el campo es negativo es decir una carga positiva allí ubicada experimentaría una fuerza haca la izquierda por tanto el campo eléctrico va hacia la izquierda (por ser negativo); en la región intermedia el campo va hacia la derecha (positivo), se vuelve cero (0) en un punto para después ir hacia la izquierda; y la tercera zona donde el campo va hacia la derecha.
El punto donde se cruza el campo con la línea cero es donde la fuerza eléctrica sobre una carga sería nula, es un punto de equilibrio estable para una carga positiva e inestable para una carga negativa.
Ejemplo 2: Dadas tres cargas q y un punto (x, y) hallar la magnitud y dirección del Campo Eléctrico y representarlo en ese punto.
Solución Mathcad:





Figura 3. Programa Elec_coul.mcad para representar el campo eléctrico generado por varias cargas en un punto dado (el rombo es el final de la flecha que lo representa).
En la figura 3 se muestran tres cargas ubicadas en un plano y el campo eléctrico generado por las mismas en un punto dado. Los estudiantes deben cambiar las posiciones (x, y) y ajustar la escala para observar gráficamente la dirección del campo eléctrico, y observar los resultados numéricos para la magnitud y dirección del campo eléctrico (magnitud total, el valor de sus componentes y el ángulo que forma con el eje x). Hacer estos cálculos a mano incluso con calculadora para varios puntos (x, y) es una tarea poco atractiva mientras que en el computador se hacen los cambios y listo, se observan resultados se prueban las hipótesis y se sacan las conclusiones pertinentes.
Ejemplo 3: Visualizar el potencial eléctrico para un sistema de tres cargas:
Solución: El potencial eléctrico
producido por un conjunto discreto de cargas esta dado por la siguiente
ecuación ![]() Donde K
es una constante, qi representa cada una de las cargas eléctricas
y ri representa la distancia de la carga qi al punto
donde calculamos el potencial. A diferencia del campo eléctrico
el potencial eléctrico es un escalar. Veamos el programa Mathcad.
Donde K
es una constante, qi representa cada una de las cargas eléctricas
y ri representa la distancia de la carga qi al punto
donde calculamos el potencial. A diferencia del campo eléctrico
el potencial eléctrico es un escalar. Veamos el programa Mathcad.



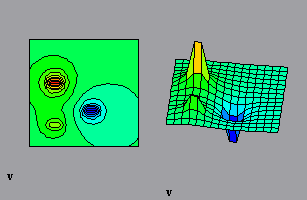
Figura 4. Programa pot_ele.mcd, Curvas de nivel y de superficie para el potencial eléctrico
Al lado izquierdo de la fig. 4. Se muestra la gráfica de curvas de nivel para el potencial, cada curva representa el mismo potencial, por tanto se tienen las curvas EQUIPOTENCIALES.
En la gráfica derecha de la figura 4, se muestra una curva de superficie en la que nos podemos imaginar, a una carga positiva como, una esferita en ese terreno y sabríamos fácilmente en que dirección se movería, esas direcciones corresponden a lo suelen llamar los textos como "líneas de campo eléctrico" que como sabemos no es mas que el gradiente del potencial.
Conclusiones
La enseñanza actual está siendo influenciada por las nuevas tecnologías, particularmente la informática. En el caso particular de la enseñanza de la Física es posible el uso de programas "software" de diferentes niveles:
![]() Referencias
Referencias