
Mathcad 8 (En español)
Por
Medardo Fonseca
mefle@yahoo.com
Apartes sobre la conferencia, ( patrocinada
por Software-Shop).
Dada en La Universidad Javeriana, Bogotá - Colombia, Julio 1 de
1999 en el
V Encuentro Nacional sobre la Enseñanza del Cálculo
¿Qué es Mathcad?
Mathcad es un ambiente para la solución de problemas, con una amplia variedad de herramientas y soporta una gran variedad de técnicas de análisis y visualización.
El programa es de amplio uso en disciplinas como en Ingeniería, Arquitectura, Química, Física y Matemáticas entre otras.
Mathcad es la combinación de:
Las tareas en Mathcad pueden realizar Cálculos y documentos en un proceso integrado.
En Mathcad se trabaja como lo haríamos
en nuestro cuaderno de trabajo, inicialmente aparece una hoja
blanca en la que podemos escribir el enunciado del problema (texto),
a continuación escribimos los datos del problema (asignamos
valores a algunas variables), escribimos las ecuaciones
pertinentes (de acuerdo al modelo en que enmarquemos en el
problema), escribimos el nombre de la variable que nos interesa
conocer su resultado, el signo igual (=) y listo, también
podemos colocar la gráfica de alguna de las variables
dependientes con los comentarios necesarios.
3.2.1.2. Una Página Típica

se muestra una página de Mathcad donde se combinan ecuaciones, texto y gráficas
Unidades
Mathcad tiene un soporte de unidades incorporado, Podemos mezclar unidades y Mathcad hace las transformaciones pertinentes, veamos un par de ejemplos:
Unidades de longitud:
![]()
Unidades de Fuerza:
![]()
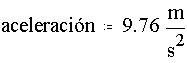
![]()
![]() Obsérvese la respuesta en Newtons
Obsérvese la respuesta en Newtons
Al combinan unidades de distinto tipo (como longitud y velocidad), Mathcad no ejecuta la operación, la ecuación cambia a color rojo y al colocar el cursor en ella , despliega una advertencia de unidades incompatibles
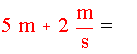
3.2.1.4 Cálculos
La manera de asignar valores a las
variables de Mathcad y solicitar resultados es muy intuitiva y la
presentación es visualmente agradable como se muestra en la
figura 3.2 y 3.3.
 |
Asignaciones
con :=
Solicitando resultados con =
(Mathcad permite incorporar gráficos explicativos). |
Fig. 3.2. ejemplos de cálculos con Mathcad

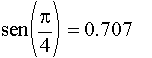
![]()
![]()
Fig. 3.3. ejemplos de cálculos con Mathcad
3.2.1.5 Cálculo simbólico
Mathcad usa un procesador simbólico que reconoce los operadores para derivadas, integrales, y limites, así resulta muy útil para despejar alguna variable de interés (ver fig 3.4).

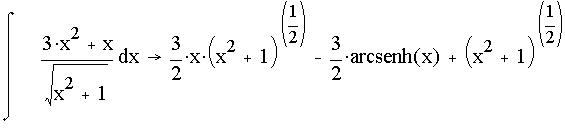

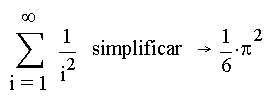
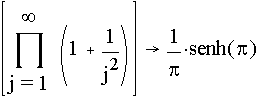
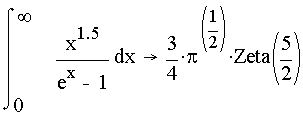
Fig. 3.4. ejemplos de cálculos simbólicos con Mathcad
3.2.1.6. Vectores y Matrices
La presentación visual de vectores y matrices hacen de Mathcad un programa ideal para el uso de estos en Física (ver Fig. 3.5).
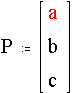
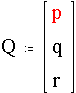

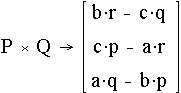
Fig. 3.5. Vectores con Mathcad
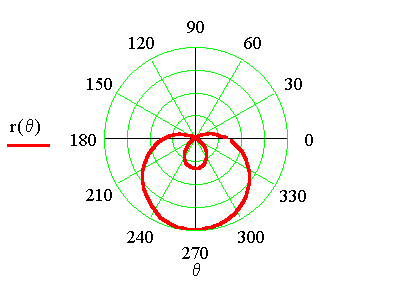
3.2.1.7. Gráficas
La habilidad gráfica de este programa permite que tan solo definamos los rangos de las variables independientes, definamos las funciones (inclusive a trozos) y visualicemos de inmediato su dependencia, en física esto es muy importante para el estudio y análisis de parámetros de un sistema (Es posible ampliar una parte de la gráfica o monitorear los valores x, y )
Las versiones
recientes de Mathcad, permiten hacer gráficas 2D (rectangulares,
polares) y 3D (superficie, Nivel, de campos vectoriales, de
dispersión) Ver Figs. 3.6 y 3.7 :
 |
 |
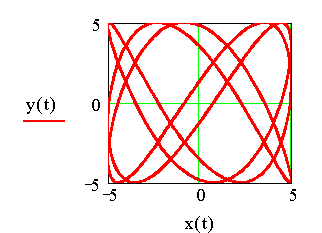 |
Fig. 3.6 Gráficas Cartesianas, polares y paramétricas-2D



![]()


Fig. 3.7 Gráficas MathCad -3D tomadas de WWW.
3.2.1.8. Programación
Con la evolución del programa, también ha evolucionado la flexibilidad para hacer programas estructurados (a partir de la versión 6) que incluyen condicionales if, ciclos For, Do e incluso mensajes de error.
En versiones anteriores 2 a 5:
![]()
![]()
En la figura 3.8 se muestra un ejemplo de programación en Mathcad para la solución de la ecuación cuadrática ax2 +bx+c = 0
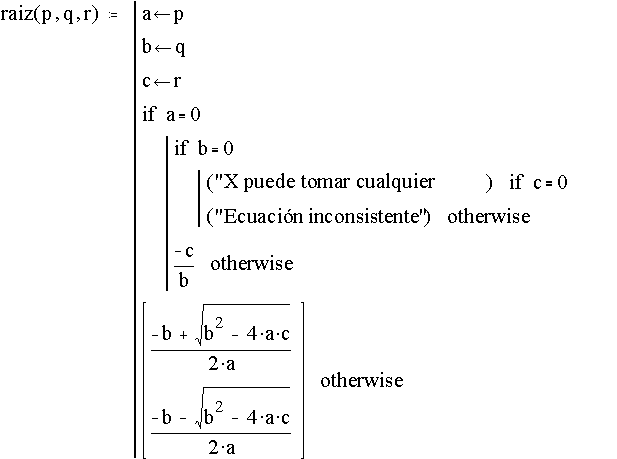

Fig. 3.8 Un programa Mathcad.
3.2.1.9. Animación - Superposición de pulsos
La variable de control de animación es "FRAME", su rango se establece al momento de hacer la animación. El resultado de la animació es un archivo .AVI, en las figuras 3.9 y3.10 se muestran las instrucciones para dibujar unos pulsos y unas imágenes de la animación resultante.
![]()
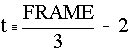
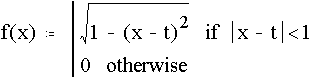
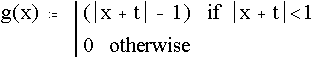

Fig. 3.9 Instrucciones en Mathcad para una superposición de pulsos y proceder a animarla.
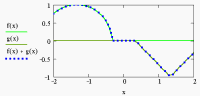

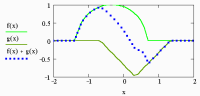
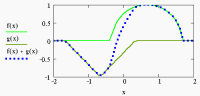
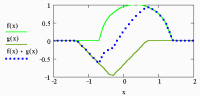

Fig. 3.10 Algunos fotogramas de la animación de la superposición de pulsos.