A Research Paper Presented by:
Murtaza Rehman (2003-02-0135)
Mohammad Omer Sheikh (2003-02-0129)
Yasir Siddique Sheikh (2003-02-0218)
Shah Rukh Mirza (2004-02-0168)
Muhammad Abdullah (2005-02-0091)
LINGUISTIC HEDGES AND APPLICATIONS OF FUZZY LOGIC TO RULE BASED SYSTEMS
ABSTRACT:
Fuzzy logic, over the past few years has turned out to be a very useful technique and phenomenon to deal with real-world and practical problems. Unlike binary logic (i.e. either 1 or 0) fuzzy logic enables us to make approximations and thus the reasoning criteria becomes more precise and comprehensive. As it is a multi-valued logic, it also allows degrees (e.g. normal versus slow or fast).
A number of practical uses of fuzzy systems have been witnessed during the past decade. The largest commercial uses for fuzzy logic are as controllers for tasks such as managing temperatures and energy efficiency in heating and cooling devices and regulating timing and fuel flow in automobile engines. Controllers also are used to make constant operating adjustments to subway trains, home appliances, cameras, and elevators.
According to David Brubaker, president of a fuzzy-logic and embedded-systems consulting firm “products designed with fuzzy logic have simpler controls, are easier to build and test, and provide smoother control than those using conventional systems.” The benefits of fuzzy logic include fault tolerance and more accurate responses to vague data.
Most of the Computer Scientists today foresee Fuzzy logic as an important tool to develop applications involving computer chips, computer graphics, software development, financial planning, information processing, sales analysis, speech recognition, machine vision, and character recognition.
All the previous attempts to measure complexity relied on sharp boundaries between what is and what is not complex. The biggest gain managers have experienced after some extra-ordinary inventions in the field of this fuzzy approach is that now they can more closely model the problems in degrees such as somewhat, moderately, and highly complex.
CRISP Vs. FUZZY:
Before the invention of FUZZY LOGIC, CRISP sets were commonly used. The CRISP concept is somewhat similar to traditional or classical logic. CRISP logic and binary logic resemble in a way because in CRISP logic also either a thing is completely included or excluded from a set. Unlike the continuous nature of FUZZY sets, CRISP sets are discrete in nature.
Bart Kosko, professor of electrical engineering at the University of Southern California, says, in his book Neural Networks and Fuzzy Systems: “A Dynamical Systems Approach to Machine Intelligence (Prentice Hall, 1991), this type of multi-valued logic was first explored some 60 years ago by Jan Lukasiewicz, a Polish logician who also defined reverse Polish notation. Max Black, a quantum philosopher, furthered Lukasiewicz’s work and created the beginning of what people now think of as fuzzy-set membership functions.”
REASONING WITH FUZZY LOGIC:
The greatest advantage of fuzzy logic is the ease with which tasks may be translated into machine language. Mathematics and Advanced Probability are very useful in solving many real-world problems, but the construction of such models is difficult and the effective approaches are not often easy to derive. Apart from this, such solutions need to be complete enough to qualify for a good model solution for any practical problem. Maintainability of such models is another issue as later additions to such models is a mammoth task.
Fuzzy models, on the other hand, are a fairly straightforward translation of the linguistic
statements of a group of rules. The model begins to function roughly as soon as two or three rules are stated, and is easily refined by tuning up the sets or by addition of more rules. In practical industrial applications, the fuzzy approach tends to lead to simpler, more easily maintained code in a shorter development time than other techniques.
A FUZZY LOGIC MODEL:
The fuzzy-logic procedure consists of analyzing and defining your problem, creating your sets and logical relationships, converting your information to what are called fuzzy sets, and interpreting your model. Various criteria’s can be used to address some specific problem in the domain of Fuzzy Logic. These prerequisites include the level of vagueness present in the data (determined mathematically) and the required accuracy of the output.
Listed below are the steps which should be followed to address a Fuzzy Logic Problem:
Before the calculations are performed and some model is developed, we have to be sure that Fuzzy Logic is the right technique to deal with this problem. This is because if Fuzzy logic is not an appropriate technique then it’d be very difficult to model that problem using this phenomenon.
NATURAL LANGUAGE:
Natural language, despite its vagueness and ambiguity, is the vehicle for human communication, and it seems appropriate that a mathematical theory that deals with fuzziness and ambiguity is also the same tool used to express and interpret the linguistic character of our language. This section continues with the use of natural language in the expression of a knowledge form known as rule based systems. The decomposition of compound rules into canonical forms and the treatment of canonical rules forms as illogical propositions are addressed.
This section of the paper sets out to propose the use of fuzzy logic as the mathematical foundation of our natural language. This is so, because it is a common observation that the vast amount of the information involved in human communication involves natural language terms that by their nature are often quite vague, imprecise and fuzzy. Fuzzy sets will be employed in the numerical description of these terms and in the prescription of the connection of terms into strings of intelligible expressions.
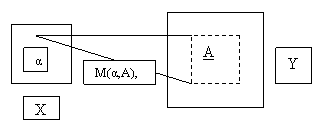
Our natural language consists of fundamental terms characterized as atoms in the literature. Let us call these terms as atomic terms.A collection of atomic terms is called a composite. Let us now define a universe, X, that contains all the atomic terms and the sets of atomic terms that exist in this universe. Now, let us define a set, Y, as a universe of cognitive interpretations, or meanings. This step might be more difficult than the development of the set X. It is quite clear that these interpretations would be rather vague, and so they might be represented as fuzzy sets.
A FORMAL MODEL OF LINGUISTICS USING FUZZY LOGIC:
Suppose we define a specific atomic term in the universe of natural language, X, as element α, and we define a fuzzy set A in the universe of interpretation, or meaning, Y, as a specific meaning for the term α. Then natural language can be expressed as a mapping, M from a set of atomic terms in X to a corresponding set of interpretations defined on universe Y. Each atomic term α in X corresponds to a fuzzy set A in Y, which is the “interpretation” of α. This mapping, which can be denoted as shown schematically in the figure below:

As an example, let us take the term “young” (α) and we want to interpret this linguistic atom in terms of age, y, by a membership function that expresses the term “young.” The membership function given here is the notation of Zadeh[1975b], and labeled A, might be one interpretation of the term young expressed as a function of age,
A=”young” = 25∫ 0 1/y + 100∫ 25 1/y (1+ ( ( y-25 ) / 5 ) 2 ) -1 .
µ M (young,y) = {( 1 + ((y-25)/5) 2 ) -1 y>25
= { 1 y ≤ 25
Now, we can define the “value” of a linguistic variable to be synonymous with its interpretation.
SET-THEORETIC OPERATIONS:
Let us define some set theoretic set operations on atomic terms, α and β that belong to the universal set X. The interpretation of the composite, defined on universe Y, can be defined by the following set-theoretic operations [Zadeh, 1975b],
α or β :µ α or β (y) = max (µ α or β (y), µ α or β (y))
α and β :µ α and β (y) = min (µ α and β (y), µ α and β (y))
Not α = 1-µ α (y)
LINGUSTIC HEDGES:
The fundamental atomic terms are often modified with adjectives or adverbs like quite, very. Slight, fairly, almost, approximately etc. These modifiers are called “linguistic hedges” in many texts. We accompany these linguistic hedges with membership functions, as the idea proposed by Zadeh. Some examples of linguistic hedges for
α = ∫ y μ α (y)/y, are given below:
“Very” α = α 2 = ∫y [ µ α ( y ) ] 2 / y . Eq 1
“Very, very α = α 4. Eq 2
“Plus” α = α 1.25. Eq 3
“Slightly” α = √x = ∫ y [ µα ( y ) ] 0.5 / y . Eq 4
“Minus” α = α 0.75. Eq 5
CONCENTRATION, DILATION AND INTENSIFICATION:
Equations 1 to 3 are called concentrations. Concentrations tend to concentrate the elements of a fuzzy set by reducing the degree of membership of all elements that are only “partly” in the set. On the other hand, equations. 4 and 5 are dilations, since they stretch or dilate a fuzzy set by increasing the membership of elements that are “partly” in the set. For example, using eq. 4 for the hedge slightly, a membership value of 0.81 is increased by 11 percent to a value of 0.9, whereas a membership value of 0.01 is increased by an order of magnitude to 0.1.
The combination of concentration and dilation is called intensification. It increases the degree of membership of those elements in the set with original membership values greater than 0.5 and it decreases the degree of membership of those elements in the set with original membership values less than 0.5. Intensification can be represented by the following equation:
“Intensity” α= = {2µ α 2 (y) for 0 ≤ µα (y ) ≤ 0.5
1 – 2[ 1 - µα (y ) ]2 for 0.5 ≤ µα (y ) ≤ 1 .
RULE BASED SYSTEMS:
In the field of artificial intelligence and expert systems, the most common way to represent human knowledge is to form it into natural language expressions o the type,
IF premise (antecedent), THEN conclusion (consequent)
This is called the IF-THEN rule-based form. If we know the antecedent, then we can derive the conclusion etc. this form of knowledge representation, characterized as shallow knowledge, is quite appropriate in the context of linguistics because it expresses human empirical and heuristic knowledge in our own language of communication. It does not, however, capture the deeper forms of knowledge usually associated with intuition, structure, function, and behavior of the objects around us simply because these latter forms of knowledge are not readily reduced to linguistic phrases or representations. We would apply the linguistic concepts and variables as its antecedents and consequents to explain the significance of Fuzzy systems and their help in the evolution of a Rule Based System, of which expert system is only a subset.
Consider the problem of the control of an industrial furnace with some restrictive statements:
The vague term “rather high” in the first statement places a fuzzy restriction on the pressure, based on a fuzzy “hot” temperature condition in the antecedent.
In summary, the fuzzy level of understanding and describing a complex system is expresses in the form of a set of restrictions on the output based on certain conditions of input. Restrictions are generally modeled by fuzzy sets and relations. These restriction statements, unconditional as well as conditional, are usually connected by linguistic connectives such as ‘and’, ‘or’ or ‘else’. The restrictions R 1, R 2, … , R r apply to the output actions or consequent rules.
DECOMPOSITION OF THE COMPOUND RULES:
A linguistic statement expressed by a human might involve compound rule structures. As an example, consider a rule-base for a simple home temperature control problem, which might contain the following rules [Vadiee, 1993]:
IF it is raining hard
THEN close the window.
IF the room temperature is very hot,
THEN
IF the heat is on
THEN turn the heat lower
ELSE
IF (the window is closed) AND (the air conditioner is off)
THEN (turn on the air conditioner)
AND (it is not raining hard)
THEN open the window
ELSE
IF (the window is closed) AND (the air conditioner is on)
THEN open the window; etc.
By using the basic properties and operations defined for fuzzy sets, any compound rule structure may be decomposed and reduced to a number of simple canonical rules as given in table I.
Rule 1: |
IF condition C 1, THEN restriction R 1 |
Rule 2: |
IF condition C 2, THEN restriction R 2 |
. . . |
|
Rule r: |
IF condition C r, THEN restriction R r |
TABLE I: The canonical form for a fuzzy rule-based system
These rules are based on natural language representations and models, which are themselves based in fuzzy sets and fuzzy logic. The following illustrates a number of the most important techniques [Vadiee, 1993] for decomposition of compound linguistic rules into simple canonical forms:
Multiple conjunctive antecedents
IF x is A 1 and A 2 … and A L THEN y is B s
Assuming a new fuzzy subset A s as
A s = A 1 ![]() A 2
A 2 ![]() …
… ![]() A L
A L
Expressed by means of membership function
μ A s (x) = min [μ A 1 (x), μ A 2 (x), … , μ A L (x)]
based on the definition of the fuzzy intersection operation, the compound rule may be written as
IF A s THEN B s
Multiple disjunctive antecedents
IF x is A 1 OR x is A 2 … OR x is A L THEN y is B L
Could be written as
IF x is A s THEN y is B s
where the fuzzy set A s is defined as
A s = A 1 ![]() A 2
A 2 ![]() …
… ![]() A L
A L ![]()
μ A s (x) = max [μ A 1 (x), μ A 2 (x), … , μ A L (x)]
which is based on the definition of the fuzzy union operation.
Conditional statements with ELSE and UNLESS
May be decomposed into two simple canonical form rules connected by “OR”:
IF A 1 THEN B 1
OR
IF NOT A 1 THEN B 2
Could be decomposed as
IF A 1 THEN B 1
OR
IF A 2 THEN NOT B 1
May be put into the following form:
IF A 1 THEN B 1
OR
IF NOT A 1 AND A 2 THEN B 2
Nested IF-THEN rules
IF A 1 THEN (IF A 2 THEN (B 1))
May be put into the form
IF A 1 AND A 2 THEN B 1
Then the rules are decomposed into a series of canonical forms, each of these forms is an implication and we can then reduce the rules to a series of relations.
TRUTH QUALIFICATION:
Primary (atomic) and composite terms using linguistic hedges may also be followed by linguistic variables connoting likelihood such as “likely”, “very likely”, “highly likely”, “unlikely” or they might be modified semantically by truth qualification statements such as “true”, “fairly true”, “very true”, “false”, “fairly false: and “very false”. These likelihood labels are based on notions of probability. The primary terms, as well as the rules, may also be restricted by linguistic variables associated with certainty, such as “indefinite”, “unknown” and “definite”. An example of a linguistic variable connoting likelihood is illustrated next.
Example [Zadeh, 1973]. We assume that the universe of discourse is given by a normalized scale,
U = ![]()
In which the elements of U represent probabilities. Suppose we wish to compute the meaning (value) of the linguistic variable ,
x = “highly unlikely”
in which “highly” and “unlikely” are defined as
“highly” = “minus very very” = (very very) 0.75
and
“unlikely” = “not likely”
With the meaning of the primary term “likely” defined on U and given by
“likely” = ![]()
we obtain
“unlikely” = “1 – likely” = ![]()
and hence
“very very unlikely” = “(unlikely) 4” = ![]()
where terms with membership values less than 0.1 have been deleted. Finally,
“highly unlikely” = “minus very very unlikely” = ![]()
= ![]()
The primary terms “yes”, “maybe” and “no” may also be assigned meanings based on membership functions given by “very very likely”, “likely” and “very very unlikely”. Note also that the atomic tem “anything” is equivalent to the universe of discourse and is given by
μ anything (x) = 1 for all x![]() X
X
Suppose we are interested in the quantification of the truth value of an antecedent or consequent in a rule [Hadipriono and Sun, 1990]. Let τ be a fuzzy truth value, for example, “very true”, “true”, “fairly true”, “fairly false”, “false”, etc. Such a truth value may be regarded as a fuzzy element on the unit interval that is characterized by its own membership function. A truth qualification proposition can be expressed as “x is A is τ”. The transformation for such propositions can be given by
x is A is τ = μ A(x τ) (1)
The above equation has the effect of reducing the membership values of the antecedent as qualified by the truth value, τ.
The fuzzy assignment statements such as
x is A is very true
or
y is B is very false
and fuzzy conditional statements such as
It is very true THAT if A THEN B
are transformed to a new meaning using the above equation (1). In the case of conditional statements, the fuzzy set describing the fuzzy relation A ![]() B will be transformed to a new fuzzy relation, i.e.
B will be transformed to a new fuzzy relation, i.e. ![]() .
.
APPLICATIONS OF FUZZY RULE BASED SYSTEMS:
The following are some of the applications of the Fuzzy Systems and the rule based systems that have been discussed above. It must be noted that the fuzzy rule based systems also involve the use of the linguistic hedges that have been discussed before.
To show how fuzzy procedures are applied to musical problems, we will continue with the issue of chord inversions. The choice of a chord inversion depends on many factors, the quality of sound desired, the avoidance of parallel fifths, fingering difficulties, and so forth. We begin the design process by formulating a set of rules as if...then... statements. Assume we want to choose inversions that will keep common tones where possible, that will not follow a root position with another root position, and will otherwise change inversions from time to time. The following rules state these criteria:
The order in which the rules are listed makes no difference, as we are going to test all of them and combine the results. The final answer should be a number that can be used to rotate the chord to the desired inversion: 0 to produce a root, 2 to produce first inversion, 1 to produce second.
All of these rules have a predicate (if...) and a consequent (then...). We evaluate the predicate of each rule to find out whether to add the consequent into the combined result. If the predicate is crisp (as in "if last position was root") the consequent will either be reported or not.
AUTOMATIC TARGET TRACKING:
Automatic target tracking is an essential requirement for surveillance systems employing multiple sensors, together with computer subsystems, to interpret an environment that includes both true targets and false alarms.
A so-called "tracker" is initialized for each observed target, which tries to follow its movement. The pairing of observations to trackers, and the prediction of the bearing of already-detected targets for the next time step. The latter is done by using the so-called "tracking filters". Furthermore, the initialized trackers are judged by means of a confidence factor, which is also used for their termination. As will be shown, both the tracking filter and the evaluation of the trackers can be realized by fuzzy systems.
The basic data for automatic target tracking in sonar systems is the integrated magnitude-squared response of a scanning beam in a noise field, which contains moving targets. This energy versus bearing representation will be called a "bearing spectrum" and is computed for consecutive time frames of length T (T depends on the integration time). Usually, the local maxima of the bearing spectra are determined and the corresponding bearings are interpreted as the locations of possible targets
DETECTION OF PROPELLOR SHAFT RATE AND NUMBER OF BLADES:
Passive sonar systems are designed for the reception of underwater sound emitted by unknown vessels. These sound signals are either active pulses or engine noise superimposed on ambient noise. Some of these signals are amplitude-modulated, such as the sound caused by the cavitations of a ship's propeller.
The sound signals received by a passive sonar system are, on the one hand, used for the determination of target bearing and, on the other hand, for the classification of the sound emitter. One of the components of such a system demodulates the broadband noise signal for the detection of low frequency components of the envelope signal. In this context, the spectrum of the envelope signals (demodulated signal) plays an important role. This component of the signal processing algorithms of a passive sonar system is called DEMON analysis (detection of envelope modulation on noise).
FUZZY HELICOPTER FLIGHT CONTROL:
The goal is to be able to use simple language "fly straight", "turn left", "hover", "land", etc., for control. It has already been done with a car more than 5 years ago. Of course, the current project is vastly more complex.
There are 15 state variables for the helicopter; three spatial coordinates, their velocities and accelerations, three angular coordinates and their speeds. Of these, currently only nine can be measured on the helicopter; spatial position and velocity need to be measured from Global Positioning System (GPS) satellite data that is not yet readily available in Japan.
Motion of the helicopter comes from making adjustments to collective pitch level, longitudinal stick, lateral stick, and directional pedal. General linguistic (high level) rules can be formulated such as "while hovering if the body rolls, then control the lateral in reverse", etc, and that these can then be converted into a number of fuzzy rules, such as "if delta x is Forward then delta longitudinal stick is Pull".
When a helicopter has an engine failure the pilot must decide if he should (a) try to restart the engine or (b) abandon the attempt. In the latter case he must disconnect the engine from the rotor to allow it to rotate freely and then dive forward in an appropriate manner to generate force on the rotor to keep it spinning. If this is done correctly, then near the ground he can straighten out and there will be enough lift on the rotors to allow a safe landing. It is claimed that it can be been done by using fuzzy control system.
CONCLUSION:
Despite its inability to make decisions that are not based entirely on raw data, fuzzy logic has become an essential problem-solving methodology in applied artificial intelligence. It provides a simple way to make a definite conclusion based on vague, imprecise, noisy, or missing input information. As a result, fuzzy logic has become a handy tool for modeling real-world complexity. These models are usually simpler and give more accurate results than their counterparts. For this reason, fuzzy logic technology has the potential to cut product development costs and times -- benefits that few companies can afford to ignore.
REFERENCES:
Examples of atomic terms: fast, large, beautiful etc.
Examples of composites: fast car, slow dog, beautiful building, large garden etc.
The basic motivation behind this is the definition of atomic term as a linguistic variable by Zadeh[1975a] as a fuzzy set.