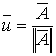Vectores

vectores III

Definición de un Vector Unitario

Se dice que un Vector es Unitario cuando su Módulo ( norma ) es igual a 1 ó a la unidad y se denota de la siguiente manera:

( Unitario )

Un Vector Unitario tiene la misma Dirección y Sentido Que otro Vector que se encuentre el Plano ó en el Espacio

En donde:

Ejemplo: Halle un Vector Unitario con la misma dirección de

Vectores Unitarios Canónicos en un Plano

Los Vectores Unitarios y se llaman Vectores Unitarios Canónicos y se denotan por:

En términos de estos Vectores, como se muestra en la siguiente figura se puede expresar cualquier vector del Plano de la siguiente forma:

En donde el Vector se llama una combinación lineal de y de , y los escalares y se llaman respectivamente, Componente Horizontal y Componente Vertical de .

Vectores Unitarios Canónicos en el Espacio

En el Espacio los Vectores se denotan como se dijo anteriormente por tríos ordenados . El Vector cero se denota por . Usando los Vectores Unitarios , , y en la dirección del eje Z, por lo tanto la notación canónica en términos de Vectores Unitarios para un Vector V es:

Naturalmente se pueden realizar operaciones con los Vectores en el Espacio.

Suma de Vectores en el Espacio ( nos da otro Vector )

Sí A es igual a y entonces

Resta de Vectores en el Espacio ( nos da otro Vector )

Sí A es igual a y entonces

Multiplicación de un Escalar por un Vector ( nos da otro Vector ) y se usa la propiedad Distributiva

Si A es igual a y se multiplica por un escalar p nos quedaría, otro Vector

Producto Escalar entre Vectores Unitarios

Ejemplos:

Definición del Producto Punto ( Escalar ó Interno )

Hasta aquí se ha estudiado tres operaciones con Vectores, la Suma y Resta de dos Vectores y la Multiplicación de un Vector por un Escalar, que dan por resultado un Vector. A partir de aquí se introducirá una tercera operación el Producto Escalar ( Punto ó Interno ) cuyo resultado no es un vector sino un Escalar ( un Número ).

Nota: El Producto Punto lo vamos a denotar por un Punto