Funciones Trigonométricas

 

 Ángulos

En geometría se considera a un ángulo como la unión de dos rayos l₁ y l₂ con el mismo punto inicial O. Si A es un punto de l₁ y B es un punto en l₂ el ángulo se denota por M AOB (figura 6.3).

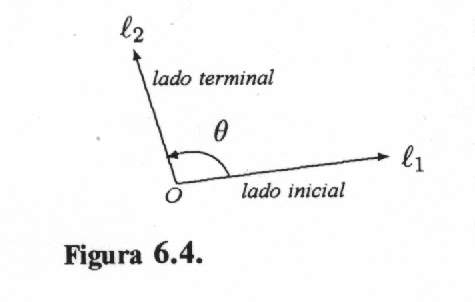
            En trigonometría los ángulos se consideran como rotaciones de un rayo. Se tiene un rayo fijo l₁ con origen O y se gira el rayo alrededor de O sobre el plano hasta otra posición

dada por el rayo l₂.

            El rayo l₁ se llama lado inicial, l₂ se llama lado terminal y O se llama el vértice del ángulo.

            Se acostumbra utilizar letras griegas para darle nombre a los ángulos. La que aparece en la figura 6.4 es q que se lee "cita", entonces el ángulo se llama ángulo cita (la flecha en la figura 6.4 indica el sentido de la rotación).

            De esta manera, la magnitud y el sentido de la rotación no se restringen y podemos

tener ángulos de cualquier medida, incluso negativos.

            Se puede hacer que el rayo l₁ de una o más vueltas antes de llegar a la posición l₂ de manera que muchos ángulos diferentes pueden tener el mismo lado inicial y el mismo lado terminal, en cuyo caso se dice que son ángulos coterminales. Por ejemplo, los ángulos de la figura 6.5 tienen todos el mismo lado inicial y el mismo lado terminal pero son distintos

.

            Para obtener el ángulo b (beta) se gira l₁ en sentido contrario al giro que se hace para obtener a (alfa) pero en ambos casos se llega al mismo l₂.

            Mientras tanto, para obtener g (gama), se hace una rotación completa en el mismo sentido de a y se sigue hasta llegar también a l₂.

            Ahora nos ubicamos sobre un sistema de coordenadas rectangulares.

Diremos que un ángulo está en posición normal si su lado inicial es la parte positiva del eje x y el origen O es el punto (0,0).

En un sistema de coordenadas rectangulares

Si el giro se hace en sentido contrario al movimiento de las manecillas del reloj se dice que el ángulo es positivo y si se hace en el mismo sentido del movimiento de las manecillas del reloj se dice que es negativo.

 

Medida de ángulos

 

En grados

Hay dos unidades muy comunes para medir ángulos. La más conocida en este nivel es la medida en grados.

            Esta se define suponiendo que si un ángulo se obtiene al girar en sentido positivo el rayol₁ exactamente una vuelta, llegando otra vez a l₁, entonces ese ángulo mide 360 grados; de manera que: un grado es la medida de un ángulo que corresponde a 1/360 de vuelta en el sentido positivo; se denota 1º.

 

En radianes

La otra forma de medir ángulos es en radianes.

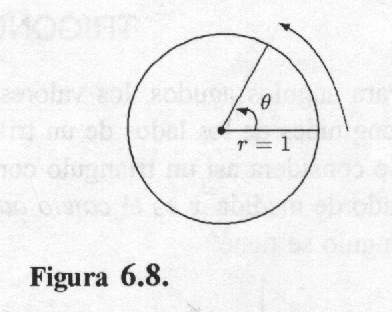
            Consideremos en el sistema de coordenadas una circunferencia con centro (0,0) y radio 1 (el llamado círculo unitario o trigonométrico) y suponga que q es un ángulo central de esta circunferencia, esto es, un ángulo cuyo vértice es el centro de la circunferencia.

La medida en radianes de q se define como la longitud del arco del sector circular determinado por q (figura 6.8).

            Según lo anterior, una rotación completa corresponde a 360º y, puesto que la medida de una circunferencia de radio 1 es 2p , entonces una rotación completa son 2p , rad. Según esto entonces se tiene que

360º = 2p rad.

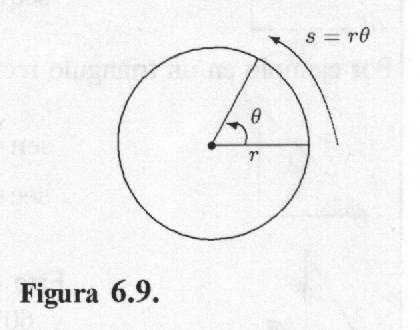
            La medida en radianes nos permite dar una fórmula simple para calcular la longitud s de un arco circular de radio r como el de la figura 6.9, esta es

longitud de arco = s = rq (q en radianes)

            Usando que 360º = 2p rad, Se deduce que:

1º = rad y 1 rad = .

y esto se usa para convertir grados a radianes y radianes a grados respectivamente.

Por ejemplo, un ángulo recto mide 90º, y expresado en radianes sería entonces

                        90º = 90 ^. rad = rad.

            En la figura 6.10 se representa algunos ángulos con sus correspondientes medidas en radianes.

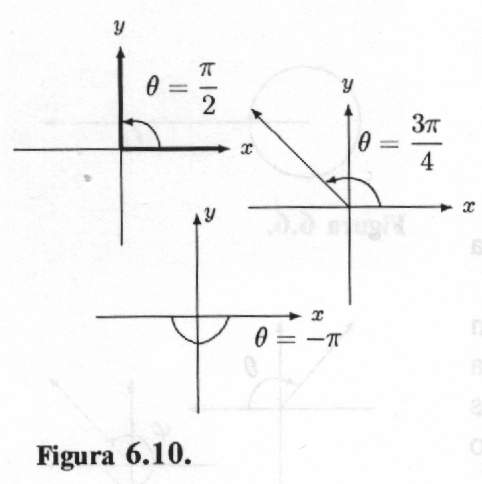
La unidad que se utiliza para medir ángulos en el Cálculo es el radián. En lo que sigue, cuando escribimos la medida de un ángulo sin hacer referencia a la unidad de medida estaremos sobrentendiendo que se trata de radianes. Por otra parte, si el ángulo q, por ejemplo, mide 2 radianes, por abuso de notación escribiremos q = 2.

            Para su mayor comodidad damos a continuación una tabla en la que aparecen algunas medidas de ángulos en grados y su equivalencia en radianes (los ángulos más usuales). Usted debe acostumbrarse a pensar en medidas dadas en radianes.

 

 TRIGONOMETRÍA EN EL TRIÁNGULO RECTÁNGULO

Para algunos ángulos agudos, los valores de las funciones trigonométricas se pueden interpretar como cocientes de las longitudes de los lados de un triángulo rectángulo.

Se considera así un triángulo como el de la figura. El lado de medida y es el cateto opuesto (cat. op.) a q, el lado de medida x es el cateto adyacente (cat. ad.) a q y el lado de medida z es la hipotenusa (hip.). Para ese ángulo se tiene:

senq = , cscq = , cosq =

secq = , tanq = , cotq =

Por ejemplo en un triángulo rectángulo cuyos ángulos agudos miden 45º se tiene:

sen 45º = , csc 45º = , cos 45º =

sec 45º = , tan 45º = = 1, cot 45º = = 1

Este es un triángulo rectángulo cuyos ángulos agudos miden 30º y 60º, a partir de él usted puede obtener todas las funciones trigonométricas de esos ángulos.

Recuadro 6.1: En el triángulo rectángulo

Tabla 6.1

Nota histórica: "p" no siempre fue p

p expresa la relación entre diámetro y circunferencia:

 = p

Se ha calculado esta relación (número) desde la antigüedad. De las primeras referencias podemos mencionar la misma Biblia: I Reyes 7, 23 y II Crónicas 4, 2. Se da un valor para p de 3 (con relación a unas medidas para el templo de Salomón alrededor del año 950 a.C.). El famoso papiro egipcio Rhind (1650 a.C.) da un valor de 3,16 para p. Estos primeros cálculos fueron hechos por medida y no por una construcción teórica.

            La primera aproximación teórica del valor de p fue dada por Arquímedes que obtuvo la relación

                        223 / 71 < p < 22 / 7

(note que el promedio de estos dos números da 3,1418: una buena aproximación).

             Las aproximaciones siguieron mejorándose durante siglos: Ptolomeo (alrededor 150 d.C.) 3,1416, Tsu Ch’ung Chi (alrededor 430 - 501 d.C.) 355/113, Al’Khwarizm (alrededor 800 d.C.) 3,1416, Al’Kashi (alrededor 1430 d.C.) una aproximación con 14 dígitos, Viète (1540 - 1603) dio 9 dígitos, Romanus (1561-1615) 17 dígitos, Van Ceulen (alrededor 1600) dio 35 dígitos. En 1873, el inglés Shanks calculó 707 dígitos, pero solo 527 eran correctos.

En 1949 con ayuda de un computador se pudo calcular 2000 dígitos para p .

            El símbolo que usamos es, sin embargo, relativamente reciente. Por primera vez fue utilizado por William Jones (1675 - 1749) en 1706. Pero la consagración de su uso fue debida al uso extenso del símbolo realizado por Leonhard Euler, el gran matemático suizo del siglo XVIII (1707 - 1783). Euler addoptó y popularizó el símbolo en 1737.

 

Definición de las funciones trigonométricas

Nos ubicamos nuevamente en la circunferencia unitaria. Según deducimos de la figura 6.11, el lado terminal de cualquier ángulo en posición normal corta a la circunferencia en un punto de coordenadas (x,y). Las seis funciones trigonométricas se pueden definir a partir de las coordenadas de este punto. Tales funciones son el seno, coseno, tangente, cotangente, secante y cosecante que se denotan respectivamente por sen, cos, tan, cot, sec y csc.

            Si q es un número real que corresponde a un ángulo en posición normal y (x,y) es el punto donde el lado terminal del ángulo corta a la circunferencia unitaria, entonces se definen las funciones trigonométricas según se indica a continuación:

 

Definición de las funciones trigonométricas

(q es un ángulo en posición normal tal que su lado terminal corta al círculo unitario en el punto P(x,y))

            Observe que el dominio de las funciones seno y coseno es todo R. Mientras tanto, en la definición de tangente y de secante aparece la abscisa x en el denominador, por lo tanto deben excluirse de su dominio todos los valores de q para los cuales x = 0; es decir hay que excluir los ángulos de medida, donde n es un número entero. El dominio de la tangente y la secante es entonces:

                                    R -

Están excluidos, por ejemplo, valores tales como:

p , -p /2, 3p /2, -3p /2, 5p /2, -5p /2

(todos los "múltiplos impares" de ).

Por otro lado, en la definición de cotangente y cosecante aparece la ordenada y en el denominador. De manera que el dominio de estas dos funciones excluye todos los valores de la forma p , con n entero. Quedan fuera, por ejemplo, los números:

                                   0, p , -p , 2p , -2p

(todos los "múltiplos de p ").

            La siguiente tabla 6.2 contiene el valor de las funciones trigonométricas para algunos valores del ángulo. Con ellos y con una serie de relaciones entre las funciones trigonométricas podemos calcular muchos valores para ellas. Pero, en general, debemos utilizar una calculadora para obtener estos valores con un ángulo cualquiera.

Tabla 6.2

Algunos valores trigonométricos
q	senq	cosq	tanq	cscq	secq	Cotq
0	0	1	0	-	1	-
				2
			1			1
					2
	1	0	-	1	-	0

 

Fórmulas trigonométricas

A partir de la definición de las funciones trigonométricas como valores referidos a las coordenadas de puntos sobre el círculo unitario se puede obtener varias fórmulas. Por ejemplo, la ecuación que define al círculo unitario es

                                   x² + y² = 1

Esto quiere decir que un punto (x,y) está sobre el círculo unitario si y solamente si satisface esa relación. Puesto que se define

                        senq = y, y cosq = x

entonces x² + y² = 1 se convierte en

sen² q + cos² q = 1 (*).

 A partir de ésta podemos deducir las que se dan a continuación:

tan² q + 1 = sec² q

1+ cot² q = csc² q.

La primera se obtiene dividiendo todos los términos de (*) por sen² q y la segunda, dividiendo los términos de (*) por cos² q.

 A continuación se dan algunas de las fórmulas trigonométricas más usuales.

tanq = , cotq = , sen (-q ) = - senq, csc (-q ) = - cscq

secq = , cscq = , cos (-q ) = cosq , sec (-q ) = secq

cotq = , tan (-q ) = - tanq , cot (-q ) = - cotq

Fórmulas para suma y resta de ángulos

           

sen (a + b) = sena cosb + cosa senb , sen (a - b> ) = sena cosb - cosa senb

cos (a + b ) = cosa × cosb - sena senb , cos (a - b ) = cosa cosb + sena senb

tan (a + b ) =              tan (a - b> ) =

sen (2a ) = 2sena cosa                                 sen² =

cos(2a ) = cos² a - sen² a                 cos² =

cos (2a) = 1- sen² a                          tan =

cos(2a) = 2cos² a -1                         tan =

tan (2a ) =

 Gráficas de las funciones trigonométricas

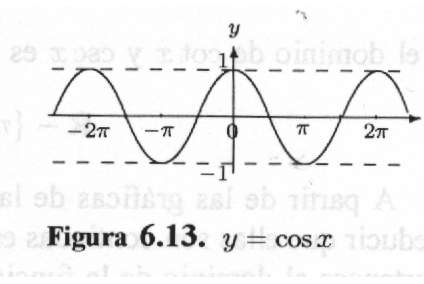
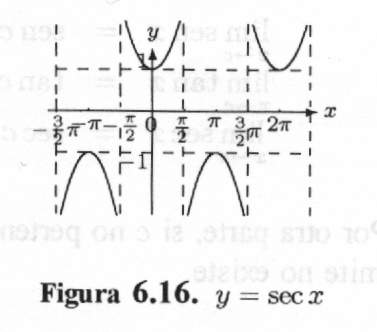
Finalizamos esta sección mostrando las gráficas de las funciones trigonométricas. Antes debemos recordar que estas funciones son periódicas, puesto que después de cada rotación completa los lados terminales comienzan a coincidir con los lados terminales de la rotación anterior y así sucesivamente. Las funciones seno, coseno, secante y cosecante tienen período 2p , las funciones tangente y cotangente tienen período p , esto es

 

Períodos de las funciones trigonométricas

sen (q + 2np ) = sen q , csc (q + 2np ) = cscq cos (q + 2np ) = cosq , sec (q + 2np ) = secq tan (q + np ) = tanq , cot (q + np ) = cot q

Los gráficos que daremos a continuación corresponden a una parte de la función y el patrón que se da se repite indefinidamente.

       

 

           

 

Una nota histórica: Las funciones trigonométricas

En los nuevos tiempos, las funciones trigonométricas fueron sistematizadas por Newton y Leibniz quienes habían dado expansiones en forma de serie para las mismas. Las fórmulas de estas funciones aplicadas a la suma y resta de ángulos fue dada por varias personas entre ellos Jean Bernoulli (1667-1798) y Thomas Fontet de Lagny (1660-1734).

            Pero fue Euler quien dio el tratamiento completo y sistemático a las funciones trigonométricas. La periodicidad de estas funciones y la introducción de la medida de los ángulos por radianes, fue realizada por Euler en su Introductio in Analysis Infinitorum de 1748.