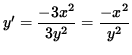 .
.
x3 + y3 = 4 Se derivan ambos lados de la ecuaciòn
D ( x3 + y3 ) = D ( 4 ) ,
D ( x3 ) + D ( y3 ) = D ( 4 ) ,
3x2 + 3y2 y' = 0 ,
3y2 y' = - 3x2 ,
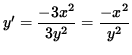 .
.
![]()
(x-y)2 = x + y - 1
D (x-y)2 = D ( x + y - 1 ) ,
D (x-y)2 = D ( x ) + D ( y ) - D ( 1 ) ,
![]() ,
,
2 (x-y) (1- y') = 1 + y' ,
2 (x-y) - 2 (x-y) y' = 1 + y' ,
- 2 (x-y) y' - y' = 1 - 2 (x-y) ,
(Factorizar respecto a y' .)
y' [ - 2 (x-y) - 1 ] = 1 - 2 (x-y) ,
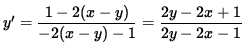 .
.
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
(Factorizando respecto a y' .)
![]() ,
,
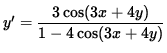 .
.
![]()
y = x2 y3 + x3 y2
D(y) = D ( x2 y3 + x3 y2 ) ,
D(y) = D ( x2 y3 ) + D ( x3 y2 ) ,
(Usando la regla del producto)
![]() ,
,
![]() ,
,
y' = 3x2 y2 y' + 2x y3 + 2x3 y y' + 3x2 y2 ,
agrupar los términos que tienen y' en un lado de la ecuación
y' - 3x2 y2 y' - 2x3 y y' = 2x y3 + 3x2 y2 ,
(Factorizar respecto a y' .)
y' [ 1 - 3x2 y2 - 2x3 y ] = 2x y3 + 3x2 y2 ,
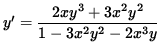 .
.
![]()
exy = e4x - e5y
D(exy ) = D ( e4x - e5y ) ,
D( exy ) = D ( e4x ) + D ( e5y ) ,
exy D( xy ) = e4x D ( 4x ) + e5y D( 5y ) ,
exy ( xy' + (1) y ) = e4x ( 4 ) + e5y ( 5y' ) ,
xexy y' + y exy = 4 e4x + 5e5y y' ,
xexy y' - 5e5y y' = 4 e4x - y exy ,
y' [ xexy - 5e5y ] = 4 e4x - y exy ,
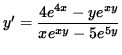 .
.
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
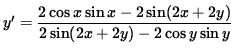 ,
,
![$ y' = \displaystyle{ 2 [ \cos x \sin x - \sin( 2x + 2y) ] \over 2 [ \sin( 2x + 2y) - \cos y \sin y ] } $](img26.gif) ,
,
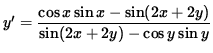 .
.
![]()
![]()
![]() ,
,
1 = (1/2)( x2 + y2 )-1/2 D ( x2 + y2 ) ,
1 = (1/2)( x2 + y2 )-1/2 ( 2x + 2y y' ) ,
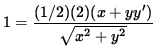 ,
,
 ,
,
![]() ,
,
![]() ,
,
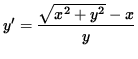 .
.
![]()
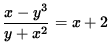 . multiplicando ambos lados por y + x2
. multiplicando ambos lados por y + x2
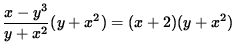 ,
,
x - y3 = xy + 2y + x3 + 2x2 .
D ( x - y3 ) = D ( xy + 2y + x3 + 2x2 ) ,
D ( x ) - D (y3 ) = D ( xy ) + D ( 2y ) + D ( x3 ) + D ( 2x2 ) ,
1 - 3 y2 y' = ( xy' + (1)y ) + 2 y' + 3x2 + 4x ,
1 - y - 3x2 - 4x = 3 y2 y' + xy' + 2 y' ,
1 - y - 3x2 - 4x = (3y2 + x + 2) y' ,
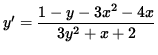 .
.
![]()
![]() multiplicando ambos lados por x3 y3
multiplicando ambos lados por x3 y3
![]() ,
,
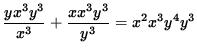 ,
,
y4 + x4 = x5 y7 .
D ( y4 + x4 ) = D ( x5 y7 ) ,
D ( y4 ) + D ( x4 ) = x5 D (y7 ) + D ( x5 ) y7 ,
4 y3 y' + 4 x3 = x5 (7 y6 y' ) + ( 5 x4 ) y7 ,
4 y3 y' - 7 x5 y6 y' = 5 x4 y7 - 4 x3 ,
y' [ 4 y3 - 7 x5 y6 ] = 5 x4 y7 - 4 x3 ,
 .
.
![]()
(x2+y2)3 = 8x2y2
D (x2+y2)3 = D ( 8x2y2 ) ,
3 (x2+y2)2 D (x2+y2) = 8x2 D (y2 ) + D ( 8x2 ) y2 ,
3 (x2+y2)2 ( 2x + 2 y y' ) = 8x2 (2 y y' ) + ( 16 x ) y2 ,
6x (x2+y2)2 + 6 y (x2+y2)2 y' = 16 x2 y y' + 16 x y2 ,
6 y (x2+y2)2 y' - 16 x2 y y' = 16 x y2 - 6x (x2+y2)2 ,
y' [ 6 y (x2+y2)2 - 16 x2 y ] = 16 x y2 - 6x (x2+y2)2 ,
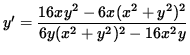 .
.
![]()
x2y + y4 = 4 + 2x
D ( x2 y + y4 ) = D ( 4 + 2x ) ,
D ( x2 y ) + D (y4 ) = D ( 4 ) + D ( 2x ) ,
( x2 y' + (2x) y ) + 4 y3 y' = 0 + 2 ,
x2 y' + 4 y3 y' = 2 - 2x y ,
y' [ x2 + 4 y3 ] = 2 - 2x y ,
![]() .
.
![]()