

Magnitudes Escalares y vectoriales
Una cantidad escalar es aquella que queda perfectamente especificada al mencionar de ella únicamente su cantidad numérica y la unidad o especie en que se mide como ejemplo tenemos: N$ 10, 35 m, 2.5 litros, 28 días, 4 naranjas, etc. En general entre las magnitudes que son escalares están: tiempo, masa, potencia, distancia, longitud, monedas, superficie, volumen, temperatura, etc.
Una cantidad vectorial es aquella que requiere, además del numeró y la unidad, mencionar su dirección, sentido y punto de aplicación para que queden perfectamente definidas. entre las principales cantidades vectoriales tenemos: Fuerza, velocidad, aceleración, desplazamiento, cantidad de movimiento, impulso, etc.
Además una cantidad vectorial se estudia y representa por medio de un vector que es una representación geométrica (generalmente un segmento de recta dirigido, o sea con una flecha en un extremo) que permite operar con este tipo de magnitudes.
Los elementos de un vector son los siguientes:
Magnitud: longitud del vector expresado por el número.
Dirección: ángulo positivo (medidoa partir de una línea horizontal de referencia y en sentido contrario a las manecillas del reloj).
Sentido: señalado por la punta de la flecha del vector.
Punto de aplicación: Indica el punto en donde inicia el vector o bien señala el punto en que se aplica la magnitud representada.
Adición de Magnitudes Vectoriales
Debido a que las cantidades vectoriales son distintas a las cantidades escalares requieren de métodos especiales para realizar su adición, entre los métodos tenemos los siguientes:
Métodos Gráficos
Método Gráfico del paralelogramo.-
El método consiste en colocar las fuerzas sobre un mismo punto de aplicación y representarlas gráficamente, al completar el paralelogramo se obtiene el resultado que esta dado por la longitud de la diagonal del mismo. Si se tuvieran más de dos cantidades se procede a trabajar por pares de cantidades vectoriales.
vector 2 vector resultante
vector 1
Método gráfico del Polígono.-
El método consiste en ir colocando los vectores uno a continuación del otro respetando la dirección y el sentido, el final de un vector es el punto de aplicación del siguiente, así hasta terminar con los vectores. El resultado de la suma es obtenido al unir el punto de aplicación del primer vector con la flecha del último vector.
Repaso Trigonométrico
C

Considerese el triángulo BAC ,rectángulo en A a
ver fig. 1 . b
Si se designan los lados con minúsculas que
correspondan a las mayúsculas de los vértices B A
opuestos,las funciones trigonométricas del c
ángulo B se pueden expresar como sigue : fig . 1
Seno es la razón del cateto opuesto al ángulo, a la hipotenusa:
sen B = cateto opuesto = b
hipotenusa a
Coseno es la razón del cateto adyacente al ángulo, a la hipotenusa:
cos B = cateto adyacente = c
hipotenusa a
Tangente es la razón del cateto opuesto al ángulo, al cateto adyacente:
tan B = cateto opuesto = b
cateto adyacente c
Cotangente es la razón del cateto adyacente, al cateto opuesto:
cot B = cateto adyacente =a cateto opuesto b
Secante es la razón de la hipotenusa, al cateto adyacente:
sec = hipotenusa = a
cateto adyacente c
Cosecante es la razón de la hipotenusa, al cateto opuesto:
csc = hipotenusa = a
cateto opuesto b
TEOREMA DE PITAGORAS a2 = b2 + c2
Método analítico de suma de vectores.
(COMPONENTES RECTANGULARES)
En este método analítico se descomponen cada una de los vectores en sus componente horizontales y verticales para adicionarlos por separado y así encontrar el vector resultante del sistema de fuerzas (Vr) y dirección (q).
Este método implica necesariamente la ubicación de los vectores (V) y sus componentes rectangulares (Vx y Vy) en un plano de ejes coordenados o plano cartesiano.
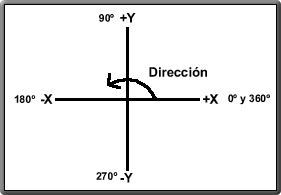
Se considera que todos los ángulos que indican la dirección de los vectores se tomaran a partir del eje de +X hacia +Y Formando ángulos hasta de 359.9999º o lo que seria lo mismo "en sentido contrario de las manecillas del reloj".
Pasos para sumar vectores por el método analítico de descomposición de vectores:
1.- Se descompone cada vector en sus componentes rectangulares Vx y Vy conservando su signo ya sea positivo o negativo según el caso utilizando las funciones trigonométricas de seno y coseno :
Vy = V sen.ø
Vx = V cos ø
2.- Después se sumaran algebraicamente (conservando su signo -+ según sea) todas las componentes rectanngulares verticales Vy y las horizontales Vx
Vxr = Vx1 + Vx2 +.......+ Vxi
Vyr = Vy1 + Vy2 +.......+ Vyi
3.-Los resultados de las sumatorias Vxr y Vyr son las componentes rectangulares horizontal y vertical respectivamente del vector resultante, entonces para encontrar este Vr y su dirección se sacaran mediante las formulas siguientes:
Vr2 = Vx2 + Vy2 vector resultante
ø = arctan(Vy/Vx) dirección del vector resultante
EJEMPLOS :
1.-Encontrar el vector resultante del siguiente sistema de vectores:
V1 = 135 Kgf , ø =35º
V2 = 95 kgf , ø = 100º
V3 = 123 Kgf , ø = 315º
Solución :
V1
Vx1=135 Kgf x cos35º = Kgf
Vy1=135 Kgf x sen35º = Kgf
V2
Vx2=95 Kgf x cos 100º = Kgf
Vy2=95 Kgf x sen 100º = Kgf
V3
Vx3 = 123 Kgf x cos315º= Kgf
Vy3 = 123 Kgf x sen315º= Kgf
Sumas :
Vxr = (Kgf)+ (Kgf)+ (Kgf)= Kgf
Vxr = Kgf
Vyr = (Kgf)+ (Kgf)+ (Kgf)= Kgf
Vyr = Kgf
Vector Resultante :
Vr2 = Vxr2 + Vyr2 = Kgf2
Vr = raíz(Kgf2)
Vr = Kgf
Dirección del vector resultante :
ø=arctan(Vyr / Vx r )
ø = °
2.-Encontrar el vector resultante y su dirección del siguiente sistema de Velocidades
V1 = 25 m/s , ø = 37.45 º
V2 = 55 m/s , ø = 88.65º
V3 = 88 m/s , ø = 75.6 º
V4 = 110 m/s , ø = 355º
V5 = 35 m/s , ø = 196º
Vr = m/s
ø = º
3.-Resolver el siguiente sistema de fuerzas encontrando su fuerza resultante y
su dirección , si una fuerza de 10 N se aplica en una dirección de 79º,otra fuerza se
aplica a 125º siendo esta de 35 N , y por ultimo una de 34 N a 270º .
4.- Una persona jala con una fuerza de 50 Kgf y una dirección de 25º una cuerda a
la que esta atada una caja , ademas ,otra persona también jala con una fuerza
60 Kgf y una dirección de 115 º y la caja se mueve ,conque dirección se movió esta
y cual fue la reacción con que se movió esta .
5.- Resuelva el siguiente sistema de Vectores encontrando su Vr y ø .
V1 = 245 N ø = 25º 37´45´´
V2 = 175,000 d ø = 351º32´
V3 = 189.2 N ø = 290º
V4 = 278 N ø = 127.50º