 camp
camp
INDICE GENERAL
1.1 Lenguajes Regulares *
1.1.1 Expresiones Regulares (ER)
*1.1.2 Equivalencia entre AFN y Expresiones Regulares *
2.1 Autómata Finito *
2.1.1 Autómata Finito Determinístico(AFD) * 2.1.2 Autómata Finito No Deterministico (AFN) * 2.1.3 Equivalencias entre los AFD's y los AFN's * 2.1.4 Autómata Finito No Deterministico con movimientos E * 3 CONCEPTO DE AUTÓMATA DE PILA (PUSHDOWN). *
3.1 Teoremas para los autómatas de pila (Push Down). * 3.2 Autómatas de Pila y lenguajes libres de contexto. * 3.3 Clasificación de Autómatas Push Down * 3.3.1 Autómatas a pila embebidos * 3.3.2 Autómatas a pila embebidos ascendentes * 3.3.3 Autómatas lógicos a pila restringidos * 3.3.4 Autómatas lineales de índices * 3.3.5 Autómatas con dos pilas * 3.4 El funcionamiento típico de un autómata pushdown. * 3.4.1 Autómata Pushdown para el reconocimiento de lenguajes libres de contexto. * 3.4.2 Obtención de una GLC a partir de un Autómata de Pila (pushdown). * 3.5 Aplicación de un Autómata Pushdown * 4 CONCLUSIONES * 5 GLOSARIO * 6 REFERENCIAS *
6.1 BIBLIOGRAFIA * 6.2 URL´s * INDICE DE FIGURAS Y TABLAS
Tabla 2.1.1 Expresiones aritméticas de longitud arbitraria (Componentes). * Figura 3.4.1.- Descripción del valor de d . * Figura 3.5.1.- Autómata de Estados Finitos para el Lenguaje de Paréntesis. * Tabla 3.5.2.- Pasos del procesamiento de la sentencia (()())# * Tabla 3.5.3.- Proceso de la sentencia ())# del Lenguaje de Paréntesis. * Figura 3.5.4.- Autómata Finito pushdown para el lenguaje de paréntesis. * Tabla 3.5.5.- Proceso de la sentencia (()())# para el lenguaje de paréntesis con el autómata Pushdown. * Tabla 4.- Proceso de la sentencia ())# del lenguaje de paréntesis con el Autómata Pushdown. *
EL MÁGICO MUNDO DE LOS AUTÓMATAS
 camp
camp
s- París- 1890
Desde la Grecia antigua existe la noción de autómata: en efecto el término
"automatos" significaba "que se mueve por el mismo" y era sinónimo de
misterio y fascinación. En Egipto por ejemplo las estatuas articuladas eran utilizadas
tanto en la política cómo en la religión.
Estas estatuas articuladas adoraban a Dios y a difuntos de importancia, con dispositivos
invisibles a los fieles, y que eran casi siempre originados utilizando aire, colocado en
vejigas de animales, que al dilatarse por pequeñas presiones hacían que se moviera la
figura.
En la historia de los autómatas, durante el siglo XVIII, se destacan
la creación de piezas excepcionales:
Los androides. Estos autómatas con formas humanas son el resultado del genio y la
habilidad de creadores magistrales como Vaucanson en Francia y Jaquet-Droz en Suiza.
Jacques de Vaucanson (1709-1782) nacido en Grenoble, tuvo desde joven
pasión por la mecánica.
Pierre Jaquet-Drotz (1721-1790) realizó entre otros el famoso "Pierrot
écrivain", un fabuloso pierrot que sentado en una mesa, y junto a una lámpara
escribe una carta interminable.
Una de las personas que en el mundo ha logrado formar una de las colecciones más interesantes de autómatas es Madame de Galéa (Madeleine de Galéa 1874- 1956). Su colección conformada por 80 espectaculares autómatas, después de su desaparición, es donada por su hijo Christian de Galéa, al Príncipe Rainiero III, en el Principado de Monáco. La misma se encuentra actualmente en el Museo Nacional de Mónaco.
1 LENGUAJES
REGULARES Y AUTÓMATA FINITO
1.1.1 Expresiones Regulares (ER)
Se denomina a un conjunto regular si puede ser generado a partir de un alfabeto £, utilizando tan solo las operaciones de unión, concatenación y cerradura de Kleene.
Definición: Sea £ un alfabeto cualquiera. Las expresiones regulares sobre £ se definen de la siguiente manera:
i) 0, E y a, ¥a E £, son expresiones regulares sobre £.
ii) Sean u y v expresiones regulares sobre £, entonces:u + v, uv y u* son expresiones regulares sobre £.
iii) Ninguna expresión que no este definida en i e ii, es expresión regular sobre £.
La notación u+ = uu*, y u2 = uu, u3 = u2u,...
ejemplo:
(a) 00
(b) (0+1)*
(c) (0+1)* 00(0+1)*
(d) (1+ 10)*
1.1.2 Equivalencia entre AFN y Expresiones Regulares
Teorema: Sea r una expresión regular. Entonces existe un AFN con transiciones-E que acepta L(r).
Demostración: Aplicando inducción sobre el numero de operadores en la expresión regular r, se muestra que existe un AFN M, con transiciones-E con un solo estado final, y con transiciones que lo pueden sacar de dicho estado; tal que L(M) = L(r).
Caso base: La expresión r debe ser E, 0 o a para algún a E £.
Inducción: (uno o más operadores)Asumimos que el Teorema es verdadero para expresiones regulares con un número de operadores menos a i, i. Sea r una expresión con i operadores. Existen tres casos:
Caso 1.- r=r1+r2 con r1, r2 que contienen menos de i operadores:
Caso 2.- r=r1r2
Caso 3.- r=r1*
entonces: L(M) = L(M1 ) Lqqd
ejemplo:
01*+1 = 0(1*) + 1
Teorema de Kleene: **Un lenguaje L es aceptado por un AFD, si y solo si, L es un
conjunto regular.
Demo: Sea L el conjunto aceptado por el AFD
M= ({q1,...,qn}, £, S, q1, F )
Sea Rkij el conjunto de todas las cadenas x tales que S(qi,x)=qj, y si S(qi,y) = qe, para cualquier y que es un prefijo de x, y E, entonces ek.
Es decir, Rkij es el conjunto de cadenas tales que pasan al autómata finito del estado qi al estado qj sin pasar por ningún estado enumerado mayor a k.
Dado que no existe ningún estado enumerado mayor que n, Rnij denota todas las cadenas van de qi a qj.
Es posible definir Rkij de una manera recursiva si procedemos de la siguiente manera:
Rkij = Rk-1ik (Rk-1kk)* Rk-1kj U Rk-1ij
{a | S(qi,a)= qj} if ij
R0ij =
{a | }S(qi,a)= qj} U {E} if i=j
Debemos demostrar, que para cada i,j y k , existe una expresión regular rkij que denota el lenguaje Rkij . Procedamos por inducción sobre k:
Base:
a1 +a2 + ....+ap si ij
roij = a1 +a2 + ....+ap + E si i=j
en donde {a1, a2 ,....,ap } son todos los símbolos de £ tales que S(qi,a) = qj
Si este es un conjunto vacío, entonces:
0 siij
roij = E sii=j
Inducción: La formula recursiva para Rkij tan solo incluye las generaciones: unión, concatenación y cerradura. Por la hipótesis de inducción, para cada l y m existe una expresión regular rlmk-1 tal que:
L(rlmk-1)= Rlmk-1
Entonces para Rijk podemos elegir la expresión regular:
(rikk-1)(rkkk-1)*(rkjk-1) + rijk-1
Lo cual completa la inducción.
Para terminar la demostración, solo debemos de observar que:
L(M) = U Rnij
Procedimiento para construir una expresión regular a partir de un autómata finito:
Entrada: Diagrama G de un autómata finito. Los nodos se numeran 1,2,....,n.
- Elija un nodo i en Gt que no sea ni nodo de inicio ni nodo final
- Elimine el nodo i de Gt, y haga lo siguiente: Por cada j,k i (es valido j=k) haga:
i) Si wji 0, wik0 y wii = 0 entonces: Agregue un arco del nodo j al k, etiquetado wji wik.
ii)Si wji0, wik0 y wii0 entonces: Agregue un arco del nodo j al nodo k etiquetado wij(wii )* wik.
iii)Si j y k tienen arcos etiquetados w1,w2,..,ws, reemplácelos por un nuevo arco etiquetado w1+w2+...+ws
iiii) Remueva el nodo i y todos los arcos que incidan sobre el en Gt.
Hasta: los únicos nodos en Gt, sean el nodo de inicio y el del estado final.
Determine la expresión aceptada por Gt.
La expresión regular aceptada por G, se obtiene al unir las expresiones de cada Gt con t.
La eliminación del nodo i se logra encontrando todas aquellas rutas j,i,k de longitud 2 que tienen i como nodo intermedio.
Este AFD acepta el lenguaje L={aibi | in}
Pumping Lemma(para lenguajes Regulares)
Sea L un lenguaje regular, que es aceptado por un AFD con k estados. Sea z una cadena en L cuya longitud |z|k. Entonces z puede ser reescrito como: z=uvw en donde: |uv|k, |v|>0 y uv2w E L, , ¥i0.
El llamado Pumping Lemma, es una herramienta poderosa para demostrar que un lenguaje no es regular.
Ejemplo:
(1) L={z E {a,b}* | |z| =n2, para algún n E N}
Supongamos que existe un AFD que reconoce L, y sea k el numero de estados que contiene. Por el Pumping Lemma, toda z E L con |z|k puede descomponerse como uv2w.
Considérese una cadena |z|=k2, por el Pumping Lemma existen u,v y w con
0<|v|
|uv2w|= |uvw|+ |v| = k2+|v|k2+k < k2 +2k +1 = (k+1)2
entonces:
|uv2w| no puede ser un cuadrado perfecto ---> L no es un lenguaje regular.
(2) El lenguaje L={ai | i es un primo} es no regular, sea n un primo y n>k, -->an = uviw
Supongamos: |uvn+1w|= |uvwvn| = |uvw| + |vn| = n + n (|v|) = n(1+|v|)
entonces:
El lenguaje es no regular
Autómata Finito.- Modelo de computación muy restringido, sin embargo tiene una gran aplicación en reconocimiento de patrones.
Representa la maquina más simple, y no contiene MEMORIA AUXILIAR. El AF, consiste de una cinta de entrada y una unidad de control.
Funcionamiento: Un AF recibe su entrada como una cadena de caracteres; dicha cadena le es entregada en la cinta de entrada. El AF no genera ninguna salida, excepto alguna SEÑAL que indique que la cadena de caracteres ha sido aceptada.
Un AF es considerado un dispositivo reconocedor de lenguaje.
El lenguaje aceptado por un AF es el conjunto de cadenas que acepta.
Para describir formalmente el funcionamiento de un AF sobre una cierta cadena, debemos
extender la definición de nuestra función de transición S, para que se aplique a un
estado, y a una cadena de caracteres, en lugar de a un solo símbolo.
Definimos así, la función: K x £* ---> K, la intención es que(q,w) represente el
estado del AF después de haber leído w, a partir del estado q.
Definición formalmente:
1)(q,E) = q
2)(¥w E String)(¥a E £) (q, wa)= ((q,w), a)
Así:(1) afirma que sin leer un símbolo, es AF no puede cambiar de estado.
Definición: Un string x se dice que es aceptado por un autómata finito M(K,£,,qo,F) si S(qo,x)=p E F.
Definición: El lenguaje aceptado por M, designado L(M), es el conjunto {x| S(qo,x)E F}.
Definición: Un lenguaje es un conjunto regular(o regular) si consiste en el conjunto aceptado por algún autómata finito.
Ejemplos:
(1) Diseñe un AF para reconocer expresiones aritméticas de longitud arbitraria que comprenden enteros positivos separados por los signos de suma, resta, multiplicación o división.
Q = {0,1}
??={0,1,2,3,4,5,6,7,8,9,+,-,· ,:}
q0 = {0}
F = {1}
(0,1+27:3-2) |--- (1,+27:3-2) |--- (0,27:3-2) |--- (1,7:3-2) |--- (1,:3-2) |--- (0,3-2) |--- (1,-2) |--- (0,2) |--- (1,?)
(2) A =
Q = {0,1,2,3}
??={a,b}
F = {3}
qo = {0}
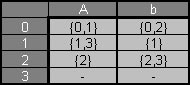
Tabla 2.1.1 Expresiones aritméticas de longitud arbitraria (Componentes).
2.1.1 Autómata Finito Determinístico(AFD)
Es un autómata finito, y es deterministico cuando su operación esta completamente determinada por su entrada.
Autómata Finito Deterministico: Es un quíntuplo: M=(K, £, S, s, F).
Donde:
k es un conjunto finito de estados (identificadores)
£ es un alfabeto finito (entrada)
s E k es el estado inicial
F subconjunto k es el conjunto de estados finales.
S: k x £ --->, es una función de transición de estados.
Una configuración es la situación en que se encuentra la máquina en un momento dado.
Definición. [q1,w1] a M [q2,w2] ssi w1=s w2 para un s Î S , y existe una transición en M tal que d (q1, s )=q2
Definición. Una palabra w Î S * es aceptada por una máquina M=(K, S , d ,s, F ) si existe un estado q Î F tal que [s,w] a M* [q, e ]
Definición. Un cálculo en una máquina M es una secuencia de configuraciones c1,c2,...,cn tales que ci a ci+1.
Teorema. Dados una palabra w Î S * y una máquina M, sólo hay un cálculo
[s,w] a M... a M[q, e ] .
Definición. Dos autómatas M1 y M2 son equivalentes, M1 » M2 , cuando aceptan exactamente el mismo lenguaje.
Definición. Dos estados son compatibles si ambos son finales o ninguno es final.
Definición. Dos estados q1 y q2 son equivalentes, q1 » q2 , si al intercambiarlos en cualquier configuración, no se altera la aceptación o rechazo de toda palabra.
Ejemplo:
AFD
Cinta de entrada
a |
B |
a |
a |
b |
b |
a |
b |
a |
Cabeza lectura
Control Finito
Características:
- Un símbolo es leído.
- La cabeza se mueve un cuadro hacia la derecha.
- El estado del AUTOMATA cambia.
Un Autómata Deterministico: NO puede mover su cabeza lectora hacia
atrás.
Una configuración de un AFD es un elemento de k x £*.
Ejemplo:
M=(K, £, S, s, F)
sean
k= {qo,q1}
£={a,b}
s=qo
F={qo}q G S(q,S)
qo a qo
qo b q1
q1 c q1
q1 d qo
Definimos una función d de KxS * ® K de la siguiente manera
d (q,e )
d (q,wa) = d ( d (q,w), a )
La intención es que d (q,w) represente al estado en que estará el AF después de leer la cadena w del estado q.
2.1.2 Autómata Finito No Deterministico (AFN)
Definición. Un AFN es un quíntuplo (K, S , D ,s, F ) donde K, S , s, F tienen el mismo significado que para el caso de los AFD, y D , llamada la relación de transición, es un subconjunto finito de k xS *x k.
Definición. Una palabra w es aceptada por AFN si existe una trayectoria en su diagrama de estados, que parte del estado inicial y llega a un estado final, tal que la concatenación de las etiquetas de las flechas es igual a w.
Definición. La cerradura al vacío de cerr-e (q) de un estado q es el conjunto más pequeño que contiene al estado q, a todo estado r ' $ una transición (p,e ,r) Î D , con cerr-e (q).
Definición. Para todo AFN existe algún AFD tal que L(N)=L(D).
Modificando el modelo del AF para que acepte cero, una o más transiciones para un mismo símbolo de entrada, obtenemos el AFN.
Una secuencia de entrada a1,a2,....an, es aceptada por un AFN si existe una secuencia de transiciones correspondientes a la secuencia de entrada, que conduce del estado inicial (a un estado final).
Como se vera mas adelante, cualquier conjunto aceptado por un autómata no determinístico puede ser aceptado por un AFN.
Un AFN se denota formalmente por un quíntuplo:
(K, £, S, qo, F) donde:
k,£,qo,Fson estados, alfabeto, estado inicial y estados finales y tienen el mismo significado que en el AF pero S:k x £ ---->2k
Ejemplo:
Un AFN que acepte todas las cadenas que contengan dos ceros consecutivos o dos unos
consecutivos.
Ejemplo: Tomando el AFND.
Q = {0,1,2,3}
??={a,b}
F = {3}
qo = {0}
Q' = {[0],[1],[2],[3],[01],[02],[03],[12],[13],[23],[012],[013],[023],[123],[0123]}
q0' = [0]
F' = {[3],[03],[13],[23],[013],[023],[123],[0123]}
Reemplazando:
[0] por q0
[01] por q1
[02] por q2
[013] por q3
[012] por q4
[023] por q5
y [0123] por q6
Ejemplo :
2.1.3 Equivalencias entre los AFD's y los AFN's
Dado que todo AFD es un AFN, es claro que la clase de lenguajes aceptado por los AFN's incluye los aceptados por los AFD. AFNAFD.
Teorema: Sea L un lenguaje aceptado por un AFN. Entonces existe un AFD que acepta L.
Demo: Sea M=(K, £, S, qo, F) un AFN que acepta el
lenguaje L.
Definamos un DFA, M'=(K', £', S', qo', F') de tal manera que:
(1) Los estados de M' son todos subconjuntos del conjunto de estados de M. Esto es: K' = 2k
= P(K) los nombres de dichos conjuntos se generara de la siguiente manera:
[q1,...,qi] E K' para {q1,...,qi} K
(2)F' es el conjunto de todos los estados en K' que contenga algún estado que
pertenezca a F.
(3) qo'=[qo]
(4)Definimos S'([q1,q2,...,qi], a) = [P1, P2,
....,Pj]
si y solo si: S({q1,...,qi}, a) = {P1, P2,
....,Pj}
Demostramos ahora por inducción sobre la longitud de la cadena de entrada, que:
S'(q0',x) = [q1,...,qi]
si y solo si: S(qo,x) = {q1,...,qi}
Demo:
1) Para |x|= 0, x=E
S'(q0',E) = [q0]
S(q0,E) = {q0}
2) H.I, |x|=m
S'(q0',x) = [r1,r2,...,rn]
<--->S(q0,x) = {r1,r2,...,rn}
3) Demostrar para |w| = |xa|= m+1
S'(q0',xa) = S'(S'(q0',x),a)
Por definición de S' tenemos:
S'([r1,r2,...,rn], a) = [P1,P2,...,Pj]
S({r1,r2,...,rn}, a) = {P1,P2,...,Pj}
Así tenemos que:
S'(S'(q0',x),a) = S'([r1,r2,...,rn] , a) =
[P1,P2,...,Pj]
<------> S(S(q0',x), a) = S({r1,r2,...,rn
}, a) = {P1,P2,...,Pj} Lqqd.
entonces AFN = AFD
2.1.4 Autómata Finito No Deterministico con movimientos E
Definición: Un autómata finito no deterministico con movimientos-E consiste en un quíntuplo (k , £, S, q0, F ) en donde K, £, q0, F se definen de la misma manera que el autómata finito no deterministico, y con:
S: K x (£ U {E})----> 2k la intención es que S(q,a)consista de todos los estados Pj, tales que existe una transición etiquetada a, desde q hasta Pj. En donde a es el símbolo E o cualquier símbolo es £.
Función de transición del ejemplo anterior:
Definición: Denominamos CERRADURA - E(q) a todos aquellos vértices (estados) Pj, tales que existe una ruta de p a q, consistente en transiciones E.
Ejemplo:
CERRADURA-E(qo) = {q0,q1,q2}
Definición: Llamamos CERRADURA-E(q) al conjunto de todos los nodos p tales que existe una ruta de q a p etiquetada E.
Es fácil extender esta definición a la CERRADURA-E(p) en donde p es un conjunto de estados:
Sea U CERRADURA-E(q), definamos como:
(1)(q,E) = CERRADURA-E(q)
(2) Para w E £* y a E £,
(q,wa)= CERRADURA-E(p)
en donde P = {p| para algún v E (q,w)y p E S(r,a)}
Es conveniente extender S y a conjuntos de estados de la manera siguiente:
(1) S(R,a) = Uq en R S( q ,a)
(2) (R,w)= Uq en R( q ,a)
para conjuntos de estados R.
Definamos: L(M) el lenguaje aceptado por M=(Q,£, S, q0, F) (un AFN con movimientos E):
L(M) = {w| (q0,w) ^ F 0}
Equivalencia entre un AFN y un AFN con Movimientos-E
Teorema: Si L es aceptado por un AFN con movimientos-E entonces L es aceptado por un AFN sin movimientos-E.
Demo: Sea M =(Q, £, S, qo, F) un AFN con Movs-E. Construya un M' = (Q,
£, S', qo, F')
donde:
y S'(q,a) = (q , a) para q E Q y a E £. Resta demostrar por inducción sobre |x| que S'(qo,x)=(qo,a) por definición de S'.
Inducción: |x| > 1, sea x=wa, a E £ entonces:
S'(qo,wa)= S'(S'(qo,w),a)
Por hipótesis de Inducción
S'(qo,w)= (qo,w)
Sea (qo,w)=P, por demostrar S'(p,a)= (qo,wa)
S'(p,a)= U S'(q,a) = U (q,a)
Entonces, como P= (qo,w) tenemos:
3 CONCEPTO DE AUTÓMATA DE PILA (PUSHDOWN).U (q,a) = (qo,wa) por la regla z en la definición de
S'(qo,wa) = (qo,wa)
Un autómata de pila (APN) es una máquina de estados finito al que se le añade una memoria externa en forma de pila (stack), es decir que sólo acepta operaciones meter (push) y sacar (pop).
Definición: Un autómata de pila es un autómata finito más una pila. Se de definen por la a tupla
M = (Q; P ; ¡; ±; q0; Z0; F)
donde Q; P,S , q0 y F se definen igual que en un AFN. G es un alfabeto de los caracteres que pueden introducirse a la pila, y Z0 es el símbolo inicial en la misma, generalmente l (significa pila vacía), pero en ocasiones es útil usar otro símbolo. La función de transición es definida como:
es decir que el cambio de estado ya no sólo depende del estado y del símbolo en la entrada, sino además del contenido de la pila, específicamente del símbolo en el tope de la pila. El contenido de la pila puede cambiar después de cada transición.
Para clarificar a la función de transición, analicemos la parte por parte:
Q x (S È {l } ) x (G È {l } ): Esta nos dice que los elementos del dominio son tercias (estado, alfabeto, pila)
[Q x (G È {l })]*:Indica que el codominio son varios pares del tipo (estado, pila)
Ejemplo 63 d (qi, a, A) = {[ qJ, B ] } Para realizar esta transición es necesario estar en el estado qi, estar analizando una a en la cadena de entrada y tener en el tope de la pila una A. Al realizarse la transición pasamos del estado qi al qJ , se procesa el símbolo a, sacamos A de la pila y metemos B .
Transición (qi, a, A) = {( qj, B)}
En el diagrama de transición, A/B significa que se reemplaza una A en el tope de la pila por una B. El significado de l ¸ es de cuidado especial, ya que en ocasiones puede significar "pila vacía", pero más generalmente significa "no importa lo que hay en la pila". Existen tres transiciones especiales que generan una acción en particular, estas son:
3.1 Teoremas para los autómatas de pila (Push Down).
Definición: Un AP determinista se define como el AP (K,S ,G ,D ,s,F) tal que para cada tripleta (p,x,y) en KxS xG , existe una y solo una transición en D de la forma (p,u,v;q,z), donde (u,v) Î { (x,y),(x, e ),(e ,y),(e ,e ) }, q Î K, z Î G
Teorema. Si L1 es un LLC y L2 es un LR, entonces L1 Ç L2 es un LLC.
Teorema. Todo lenguaje aceptado por un AF es también aceptado por un AP.
Teorema. Si L es un LLC entonces hay un AP M tal que L(M)=L
De la construcción del AP descrito anteriormente, concluimos la siguiente proposición:
S® *w ssi [p,w,e ] a * [q,e ,e ]
Si L1 y L2 son LLC entonces existe un AP que acepta L1È L2
3.2 Autómatas de Pila y lenguajes libres de contexto.
Los autómatas de pila son máquinas que nos permiten aceptar lenguajes libres de contexto. Los autómatas de pila son máquinas finitas que tienen una memoria que les da la capacidad de "recordar". De esta manera es posible reconocer lenguajes del tipo aibi | i >= 0, en el que se necesita saber cuantas a’s tiene la palabra para determinar si el número de b’s es igual.
3.3 Clasificación de Autómatas Push Down
3.3.1 Autómatas a pila embebidos
En los cuales la estructura principal de almacenamiento la constituye una pila de pilas. Junto a la definición clásica se presenta una nueva formulación en la cual se elimina el control de estado finito y se simplifica la forma de las transiciones al tiempo que se mantiene la potencia expresiva. Esta nueva formulación permite diseñar una técnica de tabulación para la ejecución eficiente de los diversos esquemas de compilación para gramáticas de adjunción de árboles y gramáticas lineales de índices.
3.3.2 Autómatas a pila embebidos ascendentes
Constituyen los autómatas a pila embebidos ascendentes. En este capítulo se realiza una definición formal de los mismos, algo que no se había logrado hasta el momento. La eliminación del control de estado finito permite simplificar la forma de las transiciones, lo cual facilita la definición de una técnica de tabulación para este modelo de autómata.
3.3.3 Autómatas lógicos a pila restringidos
Las gramáticas lineales de índices constituyen un tipo específico de gramáticas de cláusulas definidas en el cual los predicados tienen un único argumento en forma de pila de índices. Aprovechamos esta característica para definir una versión restringida de los autómatas lógicos a pila adecuada al tratamiento de este tipo de gramáticas y de las gramáticas de adjunción de árboles. Dependiendo de la forma de las transiciones permitidas, podemos distinguir tres tipos diferentes de autómata, uno que permite el análisis ascendente de los índices o adjunciones, otro que permite el análisis descendente y otro que permite estrategias mixtas. En los dos últimos casos es preciso establecer restricciones en la combinación de las transiciones para garantizar que dichos autómatas aceptan exactamente la clase de los lenguajes de adjunción de árboles. Se presentan esquemas de compilación y técnicas de tabulación para los tres tipos de autómata.
3.3.4 Autómatas lineales de índices
Los autómatas lineales de índices, que utilizan la misma estructura de almacenamiento que los autómatas lógicos a pila restringidos pero con un juego diferente de transiciones. Distinguimos tres tipos diferentes de autómata: los autómatas lineales de índices orientados a la derecha para estrategias en las cuales las pilas de índices se evalúan de modo ascendente, los autómatas lineales de índices orientados a la izquierda en los cuales las pilas de se evalúan de modo descendente y los autómatas lineales de índices fuertemente dirigidos que permiten definir estrategias mixtas de análisis para el tratamiento de las pilas de índices.
Se opta por un modelo de autómata con una nueva estructura de almacenamiento. Se preserva la pila de los autómatas a pila tradicionales, a la que acompaña una pila auxiliar cuyo contenido restringe el conjunto de transiciones aplicables es un momento dado. Los autómatas con dos pilas fuertemente dirigidos permiten definir esquemas de compilación arbitrarios para gramáticas de adjunción de árboles y gramáticas lineales de índices. Por su parte, los autómatas con dos pilas ascendentes sólo permiten describir esquemas de compilación que incorporan estrategias ascendentes en lo referente al tratamiento de las adjunciones y de las pilas de índices. Se presentan las técnicas de tabulación que permiten una ejecución eficiente de ambos modelos de autómata.
3.4 El funcionamiento típico de un autómata pushdown.
Por ejemplo, el siguiente autómata de pila reconoce L(G) = {wcwR|w E (0+1)*} , es decir los palíndromes en (0 + 1)* cuyo punto intermedio está marcado con un carácter especial c:
M = ({q1,q2}, {0,1}, {RBG}, d , q1, R, q )
Donde d vale:
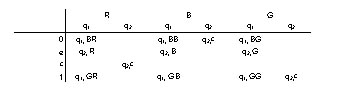
Figura 3.4.1.- Descripción del valor de d .
[q, w, a ] ^ [qj,v,b ] ^ * ^ +
Se pueden usar descripciones instantáneas para ver el funcionamiento del
autómata:
(q, aw, za ) ^ (p,w,b a )
si d (q,a,z) = (p,b ).
La cadena de un lenguaje es aceptado por el autómata si éste para en el
estado final:
L(M) = {w|(q0,w,Z0) ^ (p,e ,g ) para algún p Î F, g Î G *}
3.4.1 Autómata Pushdown para el reconocimiento de lenguajes libres de contexto.
Toda gramática GLC puede ponerse en forma normal de Greibach, en donde todas las producciones son del tipo
L -> aa donde a Î (V U T)*, a Î (T U {e }).
Método de normalización:
L i -> L jg para j > i.
Si j < i, sustituir L j por sus lados derechos. Si j = i, eliminar recursión a la izquierda, sustituyendo: L i -> L a 1 | L a 2 | ... | L ia 1 || b 1 | .... |b n | por:
L i -> b 1 | .... |b s | b 1B| .... |b s Bi
Bi -> a 1 |a 2| .... |a T | a 1Bi| a 2Bi| .... |a T Bi
Por ejemplo en:
G = ({L 1; L 2; L 3 },{a,b},P, L 1)
P : L 1 -> L 2L 3
L 2 -> L 3L 1 | b
L 3 -> L 1L 2 | a
hay que cambiar la última producción en
L 3 -> L 1L 2 | a
L 3 -> L 2L 3L 2 | a
L 3 -> L 3L 1L 3L 2 | bL 3L 2 |a
y después de eliminar la recursión a la izquierda tenemos
L 3 -> bL 3L 2B3 | aB3 | bL 3L 2 | a
B3 -> L 1L 3L 2 | L 1L 3L 2B3
Finalmente sólo nos resta sustituir en toda producción, a partir de L 3, los símbolos no terminales de la izquierda:
L 1 -> b L 3 | b L 3L 2 B 3L 1L 3 | aB3L 1L 3 | b L 3L 2L 1L 3 | aL 1L 3
L 2 -> b | b L 3L 2B3L 1 | aB3L 1 | b L 3L 2L 1 | aL 1
L 3 -> b L 3L 2B3 | aB3 | b L 3L 2 | a
B3
-> b L 3L 3L 2 | b L 3L 2B3L 1L 3L 3L 2 | aB3L 1L 3L 3L 2 | b L 3L 2L 1L 3L 3L 2 | aL 1L 3L 3L 2| b L 3L 3L 2B3 | b L 3L 2B3L 1L 3L 3L 2B3 | aB3L 1L 3L 3L 2B3 | b L 3L 2L 1L 3L 3L 2B3 | aL 1L 3L 3L 2B3Sea G = (V, T, P, S) una GLC en forma normal de Greibach que acepta L(G). Existe un APN M = ({q0, q1},S ,V U S d ,qo, e , {q1}) con transiciones:
d (q0, a, e ) = {[q1, w]|S -> aw Î P}
d (q1, a, L ) = {[q1, w]| L -> aw Î P y L Î V}
d (q0, e , e ) = {[q1, e ]} si S -> e Î P
d (q1, a, a) = {[q1, e ]} si L -> g Î P, y g } contiene a
Prueba:
Primero mostremos que L Í L (M). Sea SÞ uw con una derivación con uÎ S +yw Î V*, debemos probar por inducción que M puede derivar
[ q0, u, e ] ^ [ q1, e , w]
En el caso base (longitud uno), S Þ aw corresponde a la regla S Þ aw.
Supongamos que para todo string uw generado por SÞ n uw existe un cálculo en M
[ q0, u, e ] ^ [ q1, e , w]
Sea S Þ n+1 uw una derivación con u=va Î S +y w Î V*. Esta derivación puede ser escrita como:
SÞ n vL w2 Þ uw
donde w=w1w2 y L Þ aw1 es una regla en P. La hipótesis inductiva y la transición
[q1, w1] Î d (q1, a, L ) se combinan para producir el cálculo
[q0, va, Î ] * [q1, a, L w2] ^ [q1,Î , w1w2]
Por cada string u Î L la aceptación es exibida por el cálculo en M correspondiente a la derivación SÞ u. Para completar la demostración (L(M) Í L) hay que mostrar que para cada cálculo:
[q0, u, Î ] ^ [q1, a , L w2]
hay una derivación correspondiente S Þ uw en G.
Ejemplo
Sea G = (V, T, P, S) una gramática con la siguiente producción:
EÞ E + E | E * E | (E) | id | num
En forma normal de Greibach tenemos las siguientes producciones:
E Þ (E) | id | num | (E) B | idB | numB
B Þ +E | *E | +EB | *EB
Aplicando las reglas de transformación:
d (q0,(,e ) = { [ q1, E] , [ q1, E) B ] }
d (q0,id,e ) = { [ q1, e ] , [ q1, B] }
d (q0,num,e ) = { [ q1, e ] , [ q1, B] }
d (q1,+,B) = { [ q1, E] , [ q1, EB ] }
d (q1,*,B) = { [ q1, E] , [ q1, EB ] }
d (q1,(,E) = { [ q1, E] , [ q1, E) B ] }
d (q1,id,E) = { [ q1, e ] , [ q1,B ] }
d (q1,num,E) = { [ q1, e ] , [ q1,B ] }
d (q1, ) , ) ) = { [ q1, e ] }
Veamos cómo M acepta una expresión, por ejemplo:
(q0, id, (id*num), e ) ^ { ( q1+ (id * num ) , e ) , (q1, + (id*num), B ) } ^
{(q1, (id*num), E ), ( q1, (id * num ) , EB ) } ^
{(q1, id*num), E) ), ( q1, id * num ) , E ) B ) } ^
{(q1,*num), )) , ( q1,* num) , )B ), (q1,*num), B )), ( q1, * num ) ,B) B) } ^
{(q1,num), E )) , ( q1, num) , EB )), (q1,num), E) B ), ( q1, * num ) ,EB) B) } ^
{(q1, ) , )) , ( q1, ), B )), (q1,), ) B ), ( q1, ) ,B) B), (q1, ) ,B)) , ( q1, ), BB )),
( q1, ) ,B) B), (q1,), BB ) B } ^ {(q1, e , e ) , ( q1, e , B ) }
3.4.2 Obtención de una GLC a partir de un Autómata de Pila (pushdown).
Para obtener la GLC G = (V, T, P, S) correspondiente a un APN M, hay que crear primero un APN extendido M´ con d ´ construida a partir de d a la que se le añade:
1. Si [ qj, e ] Î d ( qi, u, e ) entonces [ qj, L ] Î d ´ (qi, u, L ) para toda L Î G .
2. Si [ qj, B ] Î d ( qi, u, e ) entonces [ qj, BL ] Î d ´ (qi, u, L ) para toda L Î G .
El alfabeto de entrada de G es el alfabeto de entrada de M´. Las variables de G consisten de un símbolo inicial S y objetos de la forma < qi, L , qj > donde las q’s son los estados de M´ y L Î G È {e }. La variable < qi, L , qj > representa un cálculo que comienza en el estado qi , termina en qj y quita el símbolo L de la pila. Las reglas de G son construidas de la siguiente manera:
{< qi, L , qk >Þ x < qj, B, qk > | qk Î Q }
3. Cada transición [ qj, BL ] Î d ( qi, x, L ), donde L Î G È {e } genera el conjunto de reglas
{< qi, L , qk >Þ x < qj, B, qn >< qn, L , qk > | qk , qn Î Q }
Ejemplo
El siguiente autómata reconoce el lenguaje { ancbn | n ³ 0}
M :
Q = { qo,q1} d ( q0,a,e ) = { [ q0, L ] }
S = { a,b,c } d ( q0,c,e ) = { [ q1, e ] }
G = { L } d ( q1,b,L ) = { [ q1, e ] }
Después de añadir las transiciones d (q0, a, L ) = { [ q0, L L ] } y d (q0, a, L )= { [ q1, L ] }, se produce la siguiente gramática:
S Þ
Simplificando tenemos:
S Þ a < q0, L , q1 > | c
< q0, L , q1 > Þ a < q0, L , q0 > < q0, L , q1 > |a < q0, L , q1 > b|cb
< q0, L , q0 > Þ a < q0, L , q0 > < q0, L , q0 > |a < q0, L , q1 > < q1, L , q0 >
|c < q1, L , q0 >
< q0, e , q0 > Þ a < q0, L , q0 > | e | c < q1, e , q0 >
< q1, L , q0 > Þ b < q1, e , q0 >
En esta gramática vemos algunas inconsistencias que hay que eliminar:
< q1, L , q0 > y < q0, L , q0 > no llevan a ningún lado
< q0, e , q0 > no es generado por nadie
por lo que hay que eliminar < q1, L , q0 > y < q0, L , q0 > donde aparezcan, por lo que la gramática queda:
S Þ a < q0, L , q0 > | c
< q0, L , q1 > Þ a < q0, L , q1 > b|cb
Obtención de una gramática de contexto libre a partir de un Autómata Pushdown sin estados finales.
Si en lugar de tener un Autómata Pushdown con estados finales como en el caso anterior tenemos un autómata Pushdown que termina cuando se vacía la pila, podemos aplicar el procedimiento explicado a continuación. Si M = (Q, S , G , d , q0, Z0, q ) es una autómata Pushdown, puede ser representado por la gramática libre de contexto G = (V, S , P, S), donde V = {< q, L , p > | q, p Î Q ^ L Î G } È {S} y P tiene las siguientes producciones:
en Q, cada a en S È {e } y L , B1, B2, ... Bm en G tal que d (q,a,L )
contiene a (q1, B1B2 ... Bm).
Ejemplo:
M : Q = {q0,q1} d (q0, 0, X) = {[q0, X X]}
S = {0, 1} d (q0, 0, Z0) = {[q0, X Z0]}
G = {X, Z0} d (q0, 1, X) = {[q1, e ]}
F = q d (q1, 1, X) = {[q1, e ]}
q0 = q0 d (q0, e , X) = {[q1, e ]}
Z0 = Z0 d (q0, e , Z0) = {[q1, e ]}
Por la primera regla se generan las siguientes producciones:
S Þ [q0Z0q0] | [q0Z0q1]
La producción d (q0, 0, X) = {[q0, X X]} genera:
[q0Xq0] Þ 0[q0Xq0] [q0Xq0] | 0[q0Xq1] [q1Xq0]
[q0Xq1] Þ 0[q0Xq0] [q0Xq1] | 0[q0Xq1] [q1Xq1]
Por d (q0,0,Z0) = {[q0Xq0] [q0,X Z0]} tenemos:
[q0Xq0] Þ 0[q0Xq0] [q0Z0q0] | 0[q0Xq1] [q1Z0q0]
[q0Xq1] Þ 0[q0Xq0] [q0Z0q1] | 0[q0Xq1] [q1Z0q1]
Por d (q0,1,X) = {[q1,e ]} tenemos:
[q0Xq1] Þ 1
Por d (q1,1,X) = {[q1,e ]} obtenemos:
[q1Xq1] Þ 1
Por d (q1, e , X) = {[q1, e ]} tenemos:
[q1Xq1] Þ e
Finalmente, por d (q1,e ,Z0) = {[q1,e ]} obtenemos:
[q1Z0q1] Þ e
Podemos eliminar las producciones (??b,??b) pues contienen [q1Z0q0] o [q1Xq0] los cuales no generan terminales. Al hacerlo, esas producciones no terminan, por lo que deben eliminarse completamente (??a,??a), así como las producciones relacionadas. La gramática resultante simplificada es:
[q0Z0q1] Þ 0[q0Xq1]
[q0Xq1] Þ 1 | 0[q0Xq1] [q1Xq1]
[q1Xq1] Þ 1 | e
3.5 Aplicación de un Autómata Pushdown
El autómata para procesar un lenguaje del tipo 2 o Lenguaje de contexto libre es llamado
Autómata Finito Pushdown (PDFA). El elemento pushdown permite que este tipo de autómata pueda procesar las sentencias más complejas que puedan resultar de un lenguaje de contexto libre. En otras palabras, una de las diferencias fundamentales entre un lenguaje del tipo 3 y uno del tipo 2 es la necesidad de "recordar" cuándo fue la ocurrencia de un símbolo y cuándo se generó una comparación de símbolo. Este es el caso del lenguaje de paréntesis, en el que es necesario recordar el número de paréntesis izquierdo en orden para reconocer el número de paréntesis derecho correcto. El Autómata Pushdown mantiene un stack que es usado como memoria para este propósito. En el autómata finito de estados, las transiciones entre estados se basan sólo en el estado actual y en el carácter de la cadena de entrada. EN el caso de los autómatas Pushdown la transición es una función del estado actual, el carácter actual en la cadena de entrada y el carácter actual en la CIMA del stack del autómata Pushdown.
En el lenguaje de paréntesis, es necesario no perder de vista cada paréntesis izquierdo que es encontrado, además de cuándo se ha encontrado un paréntesis derecho después en la sentencia. Esto puede hacerse poniendo una marca en el stack del Autómata Pushdown cada vez que se encuentra un paréntesis izquierdo. Cuando se encuentra un paréntesis derecho en la sentencia de entrada, se hace una transición de estado se hace solo si el stack tiene la marca correspondiente; y en caso contrario, entonces la sentencia no es parte del lenguaje de paréntesis.
Si el ultimo estado del autómata pushdown no es un estado de aceptación entonces la sentencia no es parte del lenguaje.
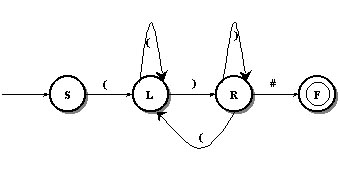
Figura 3.5.1.- Autómata de Estados Finitos para el Lenguaje de Paréntesis.
El primer paso del autómata del diseño de un autómata de pushdown para el lenguaje de paréntesis es desarrollar un autómata finito como el siguiente.
El autómata finito para el lenguaje de paréntesis consiste en un control de 4 estados:
el estado inicial (S), el estado para el procesamiento del paréntesis izquierdo (L), el estado para el procesamiento del paréntesis derecho (R) y el estado final (F). En este caso asumimos que una sentencia de lenguaje terminara por el símbolo (#). Este carácter final, cuando es encontrado realiza una transición desde el estado R hasta el estado F .
Pero que tipo de sentencias en lenguaje de paréntesis podrá reconocer este autómata finito por ejemplo:
El paréntesis izquierdo inicial nos indica hacer una transición desde el estado Sistemas al estado L y el siguiente paréntesis izquierdo causa una transición hacer esta al mismo estado L.
Luego el primer paréntesis derecho es procesado y se hace una transición al estado R. En el estado R si se encuentra otro paréntesis izquierdo , se hará una transición de regreso al estado L. El siguiente paréntesis derecho es procesado, y se hace una transición al estado R una vez mas. El siguiente paréntesis causa una transición en el mismo estado R. Finalmente (#) causa una transición al estado final y la sentencia es reconocida. Y la sentencia es (()()) # .
Pasos del reconocimiento de la sentencia anterior.
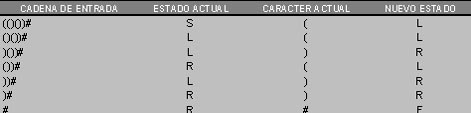
Tabla 3.5.2.- Pasos del procesamiento de la sentencia (()())#
De modo que, la siguiente sentencia a tratar es ()()) # . Esta es una sentencia invalida en el lenguaje de paréntesis porque tiene un paréntesis derecho de mas.¿ Que hará el autómata infinito con esta sentencia ? . Para esta cadena, el primer paréntesis izquierdo causa una transición al estado L del autómata. Entonces el primer paréntesis derecho produce la primera transición al estado R . Segundo paréntesis derecho coloca el autómata en el estado R . Finalmente, # causa una transición desde el estado R hasta el estado final del autómata. El proceso de esta cadena se resume en la siguiente tabla.

Tabla 3.5.3.- Proceso de la sentencia ())# del Lenguaje de Paréntesis.
El autómata acepta esta cadena, pero no es parte del lenguaje de paréntesis. Un aspecto importante del lenguaje de paréntesis es que los paréntesis izquierdos y derechos, en las sentencias están en par con otro. El autómata finito pushdown tiene la memoria necesaria para no perder de vista los paréntesis izquierdos y así es como estos son procesados en una sentencia del lenguaje de paréntesis. Al autómata finito se le aumentan operaciones de stack (PILA), para que pueda procesar elementos de una sentencia y sea capaz de no perder de vista los paréntesis. El autómata aumentado (PDFA) se muestra en la siguiente figura.
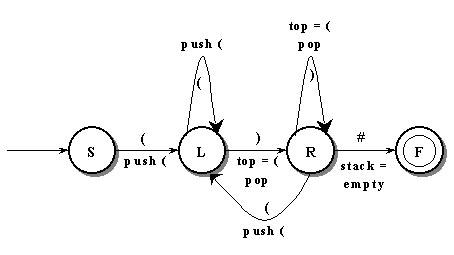
Figura 3.5.4.- Autómata Finito pushdown para el lenguaje de paréntesis.
Nótese que los arcos en este autómata tienen dos tipos de notas adicionales:
Pueden también hacer operaciones de meter y sacar de la pila (PUSH/DOWN) , o pruebas de pila (EMPTY/TOP). Las pruebas siempre se realizan antes de las operaciones. La notación en los arcos ), top=(, y pop significan que el carácter actual en proceso es un ), que la cima de la pila debe ser un (, y que si ambas pruebas son verdaderas se debe sacar el elemento de la cima de la pila. Después de esto se realiza la transición del siguiente estado.
¿Cómo procesa el autómata pushdown las cadenas del ejemplo? En el caso de la primera cadena (()()) , el primer paréntesis izquierdo causa una transición desde el estado inicial S al estado L. Una operación agregada que ocurre durante esta transición es que el símbolo (, es agregado en la pila . El segundo paréntesis izquierdo pone al PDFA en estado L , y agrega otro ( en la pila. La pila ahora contiene dos paréntesis izquierdos.
El siguiente símbolo en la sentencia es un paréntesis izquierdo. Este causa una transición al estado R si la cima de la pila contiene un paréntesis izquierdo. La cima de la pila hace entonces una transición al estado R después de que el símbolo de la cima de la pila es sacado de ella.
Luego, un paréntesis izquierdo es procesado. Una transición es hecha desde el estado R al estado L y un paréntesis izquierdo se agrega a la pila. En el estado L , el siguiente símbolo es un paréntesis derecho entonces se verifica la cima de la pila para un paréntesis derecho. La pila de la cima contiene uno y es sacado de la pila y se hace una transición desde el estado L al estado R .
La pila de la cima tiene un paréntesis izquierdo, entonces el PDFA permanece en el estado R y se saca el valor de la cima, dejando la pila vacía. La ultima transición se hace desde el estado R al estado F en la ultima sentencia # si la pila esta vacía . La pila esta vacía y se acepta la sentencia . Este proceso se resume en la siguiente tabla.
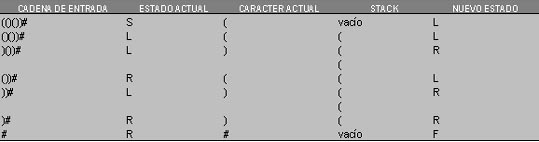
En el caso de la sentencia (()())#, el autómata Pushdown llega al estado de aceptación. ¿Llegará también al estado de aceptación con la sentencia ())#?. El primer paréntesis izquierdo causa una transición desde el estado S al estado L. Cuando ocurre esta transición, un paréntesis izquierdo es introducido en la Pila del Autómata. El siguiente símbolo, un paréntesis derecho, causará una transición desde el estado L al estado R. El paréntesis izquierdo en la cima de la pila es extraído de ésta y ocurre una transición. El próximo símbolo a procesar es otro paréntesis derecho. Para que haya una transición, se necesita un paréntesis derecho y la cima de la pila debe tener un paréntesis izquierdo. Debido a que la cima de la pila está vacía y las otras dos transiciones que salen del estado R no aplican, el Autómata Pushdown no aceptará esta sentencia. La sentencia ())# , entonces, no pertenece al lenguaje de paréntesis. Agregar la pila al autómata finito común, lo habilita para poder validar el lenguaje de paréntesis, la siguiente tabla resume el procesamiento de la cadena ())# hasta el estado donde ya no puede haber transición:

Tabla 4.- Proceso de la sentencia ())# del lenguaje de paréntesis con el Autómata Pushdown.
La primera conclusión a la que podemos llegar es que un autómata pushdown, nos sirve para procesar expresiones de lenguajes que incluyen operaciones con símbolos que van en par, como los paréntesis, y que lo que va dentro de la limitación de esos símbolos deba tener un tratamiento especial, por ejemplo, en el caso de operaciones aritméticas encerradas en paréntesis, las cuales tienen una jerarquía de precedencia mayor a las operaciones aritméticas que están fuera de los paréntesis. En el diseño de compiladores, con sus fases léxica, sintáctica y semántica, resulta de suma importancia el hecho de poder hacer que nuestro compilador sea capaz de procesar correctamente este tipo de expresiones, ya que una de las potencialidades más importantes de cualquier lenguaje es la capacidad de procesar correctamente complejas expresiones matemáticas.
El autómata pushdown, incorpora una estructura de datos que le da el poder de "recordar" la ocurrencia de un símbolo aún después de que se ha pasado a varios estados adelante, lo que le da una gran ventaja sobre un autómata finito común y permite el reconocimiento de lenguajes que incorporan operaciones con símbolos que señalan una mayor precedencia en las expresiones o que sus componentes incluyan expresiones delimitadas por algún carácter en especial.
Autómata. Es una maquina capaz de efectuar por si misma un cierto numero de operaciones previamente especificadas.
Compilador. Programa escrito generalmente en lenguaje de máquina que permite compilar.
Compilar. Producir una rutina en lenguaje máquina mediante una rutina escrita en otro lenguaje diferente a la máquina.
Extraer ( Pop ). Reemplazar el contenido de una parte específica de un palabra con las partes correspondientes de otra palabra , lo cual es determinado por algún tipo de control de patrón.
Instrucción. Conjunto de caracteres que representan una orden dada a la máquina y que esta puede cumplir.
Lenguaje. Conjunto de caracteres, símbolos, palabras, frases, instrucciones y reglas que permiten escribir y describir programas para una aplicación dada.
Lenguaje de máquina. Sistema de instrucciones que es directamente utilizable por la máquina, tal como se encuentra en la memoria principal en el momento en que está cargada.
Lenguaje de programación. Aquel que utilizan los programadores para escribir un programa en forma más o menos cómoda y que lo general requiere una traducción para ser transformado a lenguaje de máquina.
Pila. Lista de elementos a la cual se puede insertar o eliminar elementos sólo por uno de sus extremos.
1.- "Compiladores"
Alfred V. Aho
Ravi Sethi
Jeffrey D. Ullman
Ed. Addison Wesley Iberoamericana
1990, Wilmington, Delaware, EEUU
2.- "Constructing Language Proccesors
For Little Languages"
Randy M. Kaplan
Ed. John Wiley & Sons, Inc.
1994 EEUU
3.- "Introducción a la Informática"
José Luis Mora, Enzo Molino
Editorial Trillas
1979, México
http://udlapvms.pue.udlap.mx/~is103802/3.html
http://research.cem.itesm.mx/mquintan/TC/SS/Cap4.pdf
http://telelab4.iti.uned.es/Segundo/TAutomatas1.htm