The experiments on the interaction of a conductor carrying a current and a magnetic field conducted by Oersted more than two hundred years ago , have resulted in conventions that unfortunately are still colouring our perceptions of how exactly the electromagnetic field around a wire carrying a current is configured. Even when we have the means of verifying the truth or falsity of these perceptions we have failed to put right many of the previously drawn hypotheses , which a cursory examination show to be false. For instance to take one of the most damaging hypotheses on which practically the whole foundation of electromagnetism rests. Let us take the field due to a flow of current in a straight conductor. We have been told that in such a case the magnetic field , exists at right angle to the conductor , this is patently false. An examination of Fig1. Shows the experiment which was conducted to show that the magnetic field exists at right angles to the conductor.
Fig 1.

Even a little bit of thought shows that this must be wrong , these concentric circles exist at every point along the length of the conductor , they would obviously taper off towards the positive and negative poles , thus the electromagnetic field around a conductor must in fact resemble the field around a bar magnet. As shown in Fig 2
 .
.It can easily be proven , by a simple experiment that a compass placed in this field would undergo not a tangential deflection as seen in Fig 1but would align with the lines of force in a North South direction.. Thus it can be rationalized , even without resource to practical experiments , that the electromagnetic field around a straight conductor carrying a current is a solenoidal field. An argument might be made that the field seen in Fig 2 , describes the electrical field around the conductor and not the magnetic field but this is superfluous , since the field around the conductor is seen to be indistinguishable from that generated around a permanent bar magnet. Therefore the theory put forward by New Field Theory or "Aumic" theory that the "lines of force " observed around a conductor carrying an electrical current are in fact lines of linked photons which originate at the negative pole , flow through the conductor , leave the conductor at the positive pole , travel through the space surrounding the conductor and re-enter the conductor at the negative end , resulting in a continuous loop of energy, in and around the conductor , is substantiated. It is also conclusively proved that the electromagnetic field around the conductor is not as has hitherto been believed emanating at right angles to the conductor .
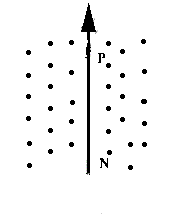
Fig 3.
According to the theory proposed by Oersted and the convention still followed today if we were to view the lines of force around an electrical conductor laid flat on the page , then the lines of force would be represented by the dots shown in Fig 3. i.e they would be coming vertically through the paper. A simple experiment shows that this is not true , if iron filings are sprinkled around a conductor positioned as shown in Fig 3 , the iron filings should (a) stand on end (b) be localised around the points indicated . What we see in fact is neither of these two phenomena , what we see is the type of formation indicated in Fig 2.
An interesting corollary to the New Field Theory , is that the energy of radiative and reactive current depends solely upon the orientation of the composite wave (i.e wave composed of chains of linked photons. ) It has already been established that according to New Field Theory (NFT) or "Aumic " theory , the photon possesses a solenoidal electromagnetic field , this enables the photon to link up in two different orientations , conduction photons can link together either in series or in parallel. In the reactive field (the field which provides electrical energy also known as the inductive field ) the photons are linked together in series or end to end in a positive to negative orientation , ( like bar magnets arranged in a line with a north to south alignment ) when this happens the composite wave-length would carry the energy of a single conduction photon , resulting in a considerable flow of energy in the conductor ( i.e an electrical current ) . If however the chain of linked photons is released from the conductor for some reason as for instance a sudden reversal of polarity the photons would undergo a movement of ninety degrees and line up laterally ( i.e bar magnets placed in a row side by side , north pole to north pole , south pole to south pole ) the composite wave-length with this orientation would carry the energy of a single conduction photon divided by the number of photons in the composite wave . ( i.e a radiative field ).
To give you an example of how this works , take for instance the ordinary house-hold supply of 60Hz. This gives a wave-length of about 5 x 10 6 m. Using the equation hc/wave-length The energy corresponding to this wave-length would be 6.62 x 10 - 34 x 3 x 10 8/ 5 x 106 m = 3.972 x 10 -32 J , which is infinitesimal , about 2.47 x 10 -13 eV . Yet the current due to this field is measured in hundred of Amperes and thousands of Volts , how can there be any connection between the two ? There seems to be no connection whatever between the energy value of the composite wave energy (field )and the energy in the conductor as it is at present explained. To elaborate on this further, the energy in the field when used in an induction process results in almost the same current (98%) flowing in the secondary as was present in the primary , yet if the two conductors are separated by some distance , (say 500 m ) and the same frequency is used , the energy in the secondary conductor due to the field is hardly detectable and is in the order of milliamps . This reduction in energy is not in proportion to the inverse square law. What is actually taking place ? Using the New Field Theory explanation it is possible to see that as long as the photons are aligned in series the amount of energy delivered to the conductor does not vary, irrespective of the composite wave length. Since the wave-length of a conduction photon has been fixed at 10 -6 m. it follows that the energy delivered by each composite wave-length would remain the same. In this case it would be as follows ( (composite wave length/conduction photon wave length) x (composite wave length energy value ) = conduction photon energy value )(5x106 / 10-6 ) x (4 x 10-32 ) =19x10-20 J which is the energy of the conduction photon and is equal to about 1.9eV. Thus the orientation of the photons in the composite wave decides the amount of energy delivered to the conductor. Now if we take the radiative value of the same field the photons have been oriented laterally and the energy value at the receiving conductor (antenna ) 500m away would be the intensity value I multiplied by the energy of the composite wave i.e 6.62 x 10 - 34 x 3 x 10 8/ 5 x 106 m = 3.972 x 10-32 J (approx). which is several orders of magnitude lower than what we would have expected if conventional reasoning is used but at the same time accurately represents the radiative value.