El Atraso de los Relojes en Movimiento

(Primer desarrollo: 10 de marzo de 2003
Última modificación: 31 de marzo de 2003

En esta página quiero mostrar que los atrasos de los relojes móviles son deducibles a partir de un modelo Newtoniano para el Espacio y el Tiempo. La intención de realizar un desarrollo alternativo es la de usar una vía más compatible con lo que denominamos "sentido común", mostrando adicionalmente que distintos modelos pueden conducir a las mismas ecuaciones. 

NOTA IMPORTANTE: Debido a que los conceptos relativistas está tan arraigados, y la mención de un sistema realmente estacionario contradice el paradigma actual de la ciencia, puede ocurrir que el lector desprevenido crea que los esquemas y deducciones que presento en esta página son anacrónicos y arbitrarios. Sin embargo, como se verá en las conclusiones  presentadas al final los esquemas aquí presentados son los mismos que resultan de aplicar las ecuaciones de la RE y, como se verá, no resulta necesario desprenderse del concepto de Marco de Referencia Estacionario para obtener dichos resultados.

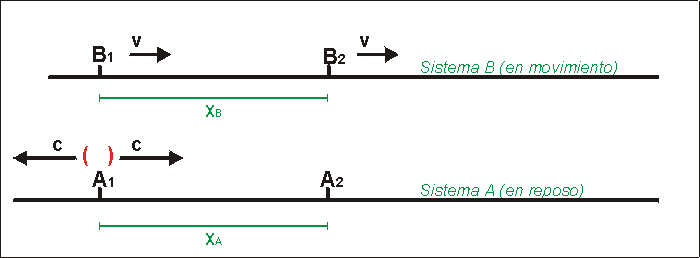
De modo que vamos a estudiar el ejemplo esquematizado en la Fig. 1, donde:

1. Suponemos que existe un Marco de Referencia Estacionario (MRE) en el que la velocidad de la luz es la misma en todas las direcciones (c = 300,000 km/seg). A efectos de clarificar el concepto el MRE se comporta en forma equivalente a una masa de aire estacionaria que hace de soporte para la transmisión de ondas sonoras. 
2. Elegimos un sistema (llamado A), que permanece en reposo con respecto al MRE.
3. Sobre el sistema A existen numerosos observadores con relojes sincronizados mediante señales luminosas. La sincronización está hecha de tal modo que una foto "instantánea", tomada con una cámara "mágica" (que recibe señales no limitadas por la velocidad de la luz) mostraría una situación como la ejemplificada en la Fig. 2.
4. Solidarios al sistema A, elegimos dos observadores A₁ y A₂, separados por una distancia X_A. En realidad A₁ y A₂ "saben" que están a dicha distancia en base el tiempo que tarda la luz (a velocidad c) en recorrer la distancia que los separa. 
5. Elegimos un segundo sistema (al que llamamos B) que se desplaza a una velocidad v con respecto al sistema A. 
6. En el sistema B identificamos dos observadores  (B₁ y B₂) que se enfrentan con A₁ y A₂ cuando los relojes del sistema A marcan el tiempo inicial del experimento (T = 0). 
7. Adicionalmente suponemos que el reloj de B₁ también marca T = 0 al enfrentarse con A₁ (Fig 2). 

En la Fig.1 se muestran dos rayos luminosos, identificados con "(   )", que parten desde la posición del observador A₁. Ambos rayos se desplazan realmente a la velocidad "c" de 300,000 km/seg en el MRE. Con respecto al sistema B, estos rayos se desplazan a la velocidad c-v en el sentido del desplazamiento de B, y c+v en sentido contrario. 

NOTA: El modelo que adoptamos tiene un Marco de Referencia Estacionario por lo que resulta válido decir que un rayo de luz se desplaza realmente a determinada velocidad. La percepción que los distintos observadores tengan de esta velocidad verdadera es lo que llamaremos velocidad aparente. En el sistema A la velocidad real y la velocidad aparente son coincidentes. Lo mismo ocurre con los tiempos y distancias. Aceptamos, por lo tanto, que las mediciones hechas en el sistema A se corresponden con los valores reales de estas magnitudes. 

La convención con respecto a valores reales y aparentes está en total desacuerdo con los conceptos relativistas, donde cada observador de un sistema inercial puede reclamar, con total derecho, que sus mediciones son las verdaderas. De todos modos, la existencia de un marco de referencia inmóvil está más en concordancia con lo que muchas personas consideran sentido común, de modo que, como señalé en las notas iniciales, mantendré el criterio ya indicado. En distintas partes de este sitio se discuten las diferencias entre uno y otro punto de vista.

La Fig. 2 muestra las lecturas de los distintos relojes en el momento en que A₁ enfrenta a B₁ y que A₂ enfrenta a B₂. Tal como se indicó, por razones de simplicidad se supone que los relojes de A₁ y de B₁ tienen lecturas coincidentes, pero no puede suponerse lo mismo para las lecturas de A₂ y B₂. 

Relación entre Coordenadas Espaciales y Temporales de ambos Sistemas

Para los observadores del sistema A, de acuerdo con la Fig.1, la distancia entre B₁ y B₂ es idéntica a la distancia entre A₁ y A₂. A esta distancia  la llamamos X_A, y, conforme a la convención que estamos empleando, ese valor es el valor verdadero de dicha magnitud.

La luz tarda X_A / c  seg en hacer el recorrido entre A₁ y A₂ y  emplea también X_A / c seg en cubrir el trayecto de Vuelta (de A₂ hacia A₁). El tiempo total que emplea la luz para realizar el trayecto de ida y vuelta entre A₁ y A₂ (que llamaremos T_0A) es, por lo tanto:

T_0A = 2 X_A / c.      [1]

Por otro lado, cuando la luz parte hacia B₂ (el rayo de la derecha en la Fig.1) recorre la distancia B₁-B₂ a la velocidad c-v, ya que el sistema móvil se está alejando de la posición (absoluta) de la que fue emitida la señal.

Por lo tanto para los observadores de A, la señal tarda.

T_1A = X_A / (c-v)          [2]

En la ecuación [2], T_1A representa el tiempo que tarda la señal luminosa en hacer el recorrido B₁-B₂, de acuerdo con los relojes de los observadores del eje A. 

Y cuando la señal retorna a B₁ emplea:

T_2A = X_A / (c+v)        [3]  

Siempre de acuerdo con las mediciones de los observadores del sistema A.

De modo que el tiempo que toma la señal en partir de B₁, alcanzar la posición de B₂ y retornar a B₁ es, según lo miden desde el sistema A:

T_3A = T_1A + T_2A = X_A / (c-v) + X_A / (c+v)              [4] 

Y, reagrupando los términos de [4], obtenemos  

T_3A = (2 X_A / c ) / (1 - v²/c² )             [5] 

En la que 2 X_A / c puede reemplazarse por su equivalente en [1], de modo de obtener

 T_3A = T_0A / (1 - v²/c² )               [6] 

Por otro lado, en la Fig. 1 identificamos como X_B al valor que obtienen los observadores del sistema B cuando miden la distancia que separa a B₁ de B₂. El valor X_B puede ser diferente del valor verdadero (X_A) de modo que (asumiendo que cualquier posible deformación de lecturas asociada al movimiento responde a una ecuación lineal) podemos escribir:

X_A / X_B = K              [7] 

Donde K es un valor a determinar.  

Primera restricción del modelo - Un dato experimental:

En base a las experiencias de Michelson y otras que emplean mediciones con recorridos de ida y vuelta del rayo luminoso, podemos establecer como hecho experimental muy sólido que:

Enunciado 1: En todos los sistemas inerciales (no sometidos a aceleraciones) se obtiene el mismo valor para la velocidad de las ondas electromagnéticas en recorridos de ida y vuelta del rayo luminoso. 

Pregunta: Éste no es el segundo postulado de Einstein sobre la constancia de la velocidad de la luz?

Respuesta: Tal como está redactado este enunciado difiere del postulado de la constancia de la velocidad de la luz en que lo que se acepta como constante no es la velocidad de la luz sino el valor numérico del cociente entre espacio recorrido y tiempo empleado por la luz durante la medición experimental.

Pregunta: Y... hay alguna diferencia importante entre ambos enunciados?

Respuesta: Si. No es lo mismo decir que la velocidad de la luz es constante, a afirmar que lo único que es constante es el resultado del cálculo. De este modo los 300,000 km/seg pueden ser el resultado de una longitud y un tiempo alterados por el movimiento.

Pregunta: Pero... es posible que las distancias y las tiempos se deformen adecuadamente para mantener un resultado constante aunque la velocidad de la luz no sea constante?

Respuesta: Si. No sólo es posible, como veremos en este desarrollo, sino que es justamente lo que debería esperarse si la velocidad de las ondas electromagnéticas estuviera ligada íntimamente a la estructura interna de la materia. Algo así planteó Lorentz para justificar el resultado negativo del experimento de MIchelson.

El enunciado 1 pone ciertas restricciones para que el modelo que estamos desarrollando sea válido. Los observadores del eje móvil deben obtener el valor c = 300,000 km/seg cuando realizan sus experiencias para medir la velocidad de la luz en recorridos de ida y vuelta. Esto equivale a afirmar que si llamamos T_0B al tiempo que tarda la luz en recorrer la distancia de B₁ hasta B₂ y retornar a B₁ (recorriendo dos veces la longitud X_B) debe cumplirse que:

2 . X_B / T_0B = c              [8] 

En [8] todos los valores están medidos por observadores solidarios al sistema B. Como ya se expresó, este resultado no significa que la velocidad de la luz es constante, sino que se obtiene un valor constante para el cociente entre un tiempo que puede estar alterado y una longitud que también puede estarlo.

Igualando los primeros términos de las expresiones [1] y [8] obtenemos

2 . X_B / T_0B = 2 . X_A / T_0A     

Donde simplificando y reordenando los términos resulta  

T_0B / T_0A = X_B / X_A             [9]

De modo que, de acuerdo con [6] 

 T_0B / T_3A = (1 - v²/c² ) X_B / X_A          [10]   

Donde reordenando términos y reemplazando X_B / X_A por su equivalente expresado en  [7]  

T_3A = T_0B. K / (1 - v²/c² )                [11] 

Siendo T_3A y T_0B los tiempos empleados en ambos sistemas para caracterizar la duración de un mismo evento (la ida y vuelta de una señal luminosa desde la posición de B₁ hasta la posición de B₂). De este modo las ecuaciones  [7] y  [11] establecen las relaciones existentes entre los valores de longitudes y tiempos medidos en ambos sistemas.

Aceptando como conocidos T_3A y X_A, entre las dos ecuaciones tenemos tres incógnitas (T_0B, X_B y  K) de modo que  existen infinitos valores de K que permiten cumplir ambas igualdades. 

Por lo tanto, para resolver el sistema con criterio físico necesitamos alguna condición adicional.

Segunda restricción del modelo - Una suposición "razonable":

Dado que la medición de la velocidad de la luz arroja un valor constante en mediciones de ida y vuelta, podemos suponer que

Enunciado 2: Los sistemas físicos se integran al universo de modo que el valor de la velocidad de la luz también arroje un valor constante para mediciones hechas en recorridos en un solo sentido (caminos de Ida o Vuelta  únicamente).

Pregunta: Qué hizo Einstein con estos valores durante el desarrollo de la Relatividad especial?

Respuesta: Postuló que ambos valores eran idénticos como base de su metodología para sincronizar relojes distantes.

Pregunta: Pero... en el modelo presentado en esta página sabemos que ambos valores son diferentes. De acuerdo con el modelo la velocidad de la luz con respecto al eje B es (c+v) o (c-v) según el sentido de desplazamiento del rayo luminoso. Cómo puede parecer que ambos tiempos son iguales?

Respuesta: Alterando las lecturas de los relojes para que los observadores del sistema B, crean que los tiempos son iguales.

Pregunta: Pero... esto es hacer trampa. Con que objeto los relojes de B se alterarían para engañar a sus propios observadores?

Respuesta: No. El planteamiento es inverso. En forma natural se deforman las lecturas de los relojes (y cosas mucho más profundas, ligadas a la estructura íntima de la realidad) de modo que los observadores en movimiento no se dan cuenta que se están moviendo. Es algo parecido a la equivalencia de sistemas inerciales planteada por Galileo. Parece una propiedad de nuestro Universo que los observadores no pueden detectar fácilmente su movimiento absoluto.

Con este nuevo enunciado podemos resolver el sistema de ecuaciones planteado.

Empecemos por determinar cuál es la lectura del reloj de B₂ si el reloj de B₁ y de A₁ tienen la misma lectura (tal como se muestra en la Fig. 2).

Para eso llamaremos:   

• T_1B al tiempo empleado por la luz para recorrer el trayecto B₁-B₂, medido en el sistema B.
• T_2B al tiempo empleado por la luz para recorrer el trayecto B₂-B1, medido en el sistema B.

De modo que 

T_0B = T_1B + T_2B           [12] 

Donde, reemplazando T_0B despejado de la ecuación  [8] resulta

T_1B + T_2B = 2 . X_B / c              [13] 

Y como la distancia a recorrer es la misma en ambos sentidos, los tiempos empleados son inversamente  proporcionales a la velocidad de la luz en cada tramo, de modo que:

T_1B / T_2B =( c+v) / (c+v)             [14] 

 Donde, despejando T_1B entre  [13]  y  [14]  obtenemos 

T_1B  =  X_B (c+v) /  c²             [15] 

De este modo, la expresión [15] establece el tiempo que tarda el rayo luminoso para recorrer la distancia B₁-B₂ en función de la velocidad del eje B y del valor asignado en dicho sistema a la distancia que separa ambos observadores.

Sin embargo conforme a nuestro segundo postulado debe cumplirse que:

T_1B = T_0B / 2              [16] 

Donde, reemplazando T_0B por su equivalente según [8], resulta:

T_1B = X_B / c              [17]

La diferencia entre el valor de T_1B calculado en las expresiones [15] y [17] tiene el siguiente significado:

• La expresión [15] muestra el intervalo de tiempo que transcurre realmente en el sistema B mientras el rayo de luz recorre el trayecto B₁-B₂.
• La expresión [17] indica la diferencia de lecturas que debe obtenerse entre el reloj de B₁ cuando parte la señal y el reloj de B₂ cuando la señal alcanza su posición para que ambos observadores coincidan en apreciar que el tiempo empleado en el trayecto de ida es la mitad del tiempo total empleado en el recorrido de ida y vuelta.

Por lo tanto, si denominamos 

• T_B0 a la lectura del reloj del origen de coordenadas en el momento que parte la señal.
• T_XBi a la lectura del reloj de B₂ ubicado a una distancia XB del origen de coordenadas, en el momento que parte la señal.
• T_XBf a la lectura del reloj de B2 en el momento en que la señal llega a B₂.

debe cumplirse, conforme a la ecuación [17]

T_XBf = T_B0 + X_B / c      [18]    

Por lo tanto T_XBi debe tomar el valor 

 T_XBi = T_B0 - X_B (c+v) /  c² +  X_B / c           [19]    

para que X_B (c+v) /  c² segundos después, su lectura sea la que indica la expresión   [18]    

En resumen. la expresión [18] indica la diferencia de lecturas que debe existir entre los relojes de los observadores B₁ y B₂ para que puedan mantener la apariencia de la constancia de c en el recorrido de la luz entre  B₁ y B₂.

T_XBi = 0 - X_B v /  c²               [20]    

Dado que hemos asumido que el reloj de B₁ marca el tiempo t=00 en el momento que parte la señal luminosa.

Y en base a  [7] puede escribirse    

T_XBi = - (X_A v /  c² ) / K         [21]    

Que expresa la lectura de cualquier reloj del eje B, a tiempo t=00 y a una distancia X_A, del origen de coordenadas de A.

Es fácil comprobar que este atraso en la lectura del reloj de B₂ con respecto al reloj de B₁ también genera un valor aparente de c para la velocidad de la luz en el trayecto de vuelta (desde B₂ hasta B₁). 

La Fig. 3 muestra la lectura de todos los relojes en el momento en que tanto A₁ y B₁ como A₂ y B₂ se enfrentan.  

Conclusiones

En este desarrollo se muestra que las ecuaciones de transformación entre longitudes y tiempos para sistemas en movimiento relativo uniforme pueden derivarse mediante un modelo "clásico" que considere la existencia de un Marco de Referencia Estacionario. 

En el desarrollo se muestra que el controvertido atraso de los relojes en movimiento puede obtenerse como resultado de exigir que la velocidad de la luz deba aparentar que toma el valor c para todos los sistemas inerciales, y no como un resultado de que la velocidad de la luz deba ser la misma para todos los sistemas inerciales.

 Volver a la página principal