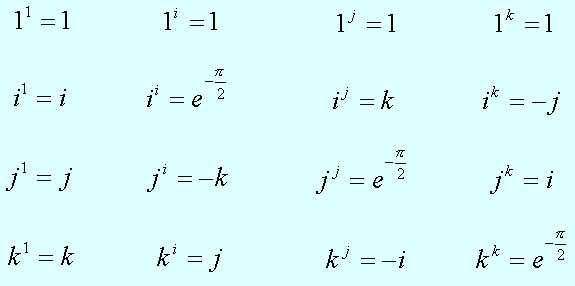
Álgebra extendida de cuaternios
Para este momento, ya debe ser evidente la forma en que puede calcularse por ejemplo el seno de un cuaternio, o su logaritmo natural. Lo único que se necesita es aplicar sistemáticamente las sustituciones de unidades imaginarias y las fórmulas de números complejos.
Sin embargo, en algunos casos se tiene que cuidar que la anticomnutatividad altera ligeramente algunas de estas fórmulas... Más adelante se aclarará esto...
A veces, puede ser auxiliar una tabla como esta:
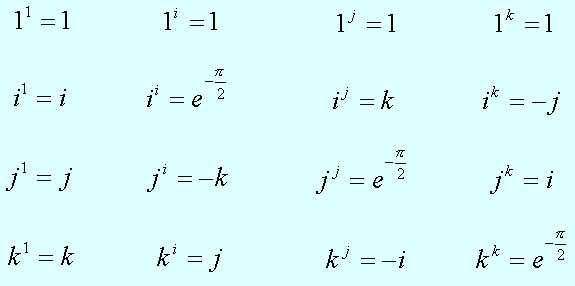
Analicemos una de estas igualdades.
Para empezar, reconsideremos la fórmula compleja:
?
Esta fórmula es totalmente válida para números complejos, sin embargo, se está obviando un paso... Tenemos la multiplicación de w y de ln(z), pero ¿en qué orden debemos efectuarla? Claramente se ve que los dos multiplicandos son cuaternios entonces sí existe una diferencia importante...
Para las exponenciaciones basadas en el producto de Grassman (que son las que estamos usando), el orden correcto es:
Ahora, para la igualdad que nos interesa tenemos:
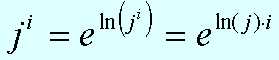
Un primer problema es calcular el logaritmo natural de j, para esto aplicamos el principio de sustitución de unidades imaginarias, y tenemos:
Ahora, debemos efectuar una multiplicación.
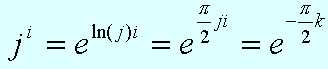
Se aplica de nuevo el principio de sustitución y...
Con lo que llegamos al resultado esperado.
Es interesante notar que 
, esto
nos lleva a que una unidad imaginaria elevada a sí misma nos da como
resultado un número real.
Recordemos que al obtener el logaritmo natural del exponente hay muchos posibles valores, así que muchas exponenciales serán multivaluadas.
También hay que tener muy en cuenta una cosa... cuando aplicamos el principio de sustitución, y cambiamos una unidad û por la muy familiar i, llegamos a un resultado complejo, en el cual debemos volver a cambiar a i por û; sin embargo, existen dos casos especiales:
a) Después de realizar la operación, i desaparece y el resultado es real.
En este caso, no importa cuál unidad û hayamos tenido en primer instancia, el resultado es real. Ejemplos son las exponenciales del tipo û^û, o û^2.
b) La función original definida en R4, sólo contiene números reales, pero el resultado es un número complejo.
En este caso, cualquier unidad imaginaria puede reemplazar a la i del resultado.
Copyright © 1999-2001 Ricardo Arturo Espinoza Reyes