Multiplicación (1/3)

La multiplicación es la operación más importante para los cuaternios, porque su sentido no es tan fácil de intuír como las sumas o restas, y de hecho a Hamilton le costó mucho trabajo lograr deducir las reglas para multiplicar a sus cuaternios.

Con el fin de ser congruente con los subconjuntos complejos y reales, la multiplicación debía cumplir con cinco propiedades principales, considerando que tenemos a los números aû y bê, donde a y b son reales y ê, û son unidades imaginarias cualquiera:

1. Si û y ê son unidades imaginarias perpendiculares, el resultado de (aû)(bê) debe ser un imaginario puro, con magnitud ab, y en una dirección perpendicular tanto a û, como a ê, y por supuesto a la recta de los reales. (De aquí la necesidad de tratar con un 4-espacio).
2. Si û = ê, entonces el resultado de la multiplicación es simplemente -ab, debido a que todas las unidades imaginarias se comportan igual ante los reales, y este caso equivaldría a multiplicar (ai)(bi). (Un caso casi evidente de este punto sería si û y ê apuntaran en direcciones opuestas exactamente. En este caso, û = -ê, y por lo tanto ûê = 1, pero por simplicidad podemos cargarle el signo a la parte real y olvidarnos de este problema).
3. El producto de (aû)(bê) debe ser un cuaternio bajo cualquier circunstancia, independientemente de las elecciones arbitrarias de los multiplicandos. Por lo tanto, de acuerdo con los puntos anteriores, si û y ê no son ni perpendiculares ni paralelas, el resultado debe tener una parte imaginaria originada por la componente ortogonal de las unidades imaginarias, que será en una dirección como la generada en el punto 1; y además habrá otra parte real generada por la componente colineal de manera similar a lo que ocurre en el punto 2.
4. Se cumple siempre que |aû|*|bê| = |ab|. Y en general, dados dos cuaternios elegidos arbitrariamente A y B, siempre será que |A|*|B| = |AB|.
5. Los cuaternios deben cumplir con respecto a los reales y a otros cuaternios colineales con las propiedades de conmutatividad, distributividad (con suma y resta) y asociatividad de la multiplicación. Esto se debe a que los reales y los complejos cumplen con estas condiciones, y son subconjuntos de los cuaternios.

Sería deseable que los cuaternios en general fueran siempre conmutativos, distributivos y asociativos; sin embargo, la quinta condicion no pide tanto. Sólo necesita preservar las propiedades en el caso de números complejos formados por unidades imaginarias iguales, o de reales.

Afortunadamente, la asociatividad y la distributividad no representan ningún problema, y pueden generalizarse traquilamente a cualquier trío de cuaternios A, B y C. Entonces, siempre ocurre que AB + AC = A(B+C), y que A(BC) = (AB)C.

Pero la conmutatividad no es tan fácil de garantizar, y consideremos entonces el siguiente ejemplo:

El resultado debe ser un real puro, según las definiciones que aparecen arriba. De acuerdo a la condición 5, el resultado debe ser el negativo del cuadrado del valor absoluto, (pues ); y la parte real es consistente con esto, pero tenemos una parte imaginaria que no podemos eliminar a simple vista. A menos que el par ij cancele al par ji, el jk al kj y el ik al ki. De aquí surge la anticonmutatividad, pues en general para dos unidades imaginarias perpendiculares û y ê, tenemos ûê = -êû.

Con estas dos condiciones, podemos llegar a la tabla de multiplicación que Hamilton empleó en 1847:

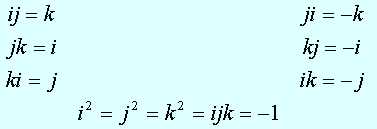
Sin embargo, notemos que esta otra tabla de multiplicar funciona exactamente igual que la anterior, y que es igual de consistente que la de Hamilton.

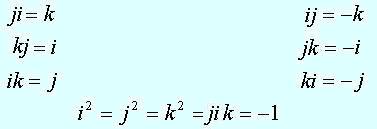
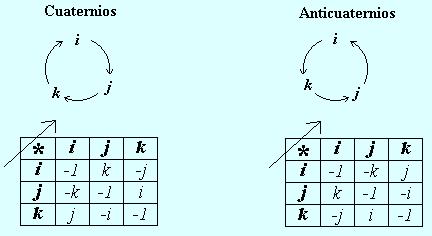
Si nos preguntamos, ¿cuál es la correcta? La respuesta es que las dos.

Debemos recordar que i, j y k son tres unidades imaginarias perpendiculares entre sí elegidas arbitrariamente, por lo tanto hay una infinidad de sistemas iguales. En todos estos sistemas, los productos ij y ji deben ser colineales a k, pues es la única dirección posible, sin embargo, podemos elegir cuál corresponde a k y cual a -k.

Sin embargo, esta elección automáticamente determina toda la tabla de multiplicar, por lo tanto sólo hay dos opciones para elegir, las cuales son idénticamente válidas; y por simple convención, llamamos a la primera: tabla de multiplicación de los cuaternios, y a la segunda: tabla de multiplicación de los anticuaternios.

A partir de ahora, no tiene caso seguir con esta dualidad, así que podemos olvidarnos de los anticuaternios por el momento, en la página correspondiente a propiedades de simetría reaparecen este sistema.

Producto de Grassman

A este producto que hemos estado analizando hasta este momento, lo llamamos producto de Grassman, y es la forma tradicional y normal de multiplicar cuaternios.

Siempre que se encuentre una multiplicación de cuaternios, complejos o reales, y no se especifique otra cosa, se entenderá que se está evaluando el producto de Grassman, y la manera de de evaluarlo es haciendo la multiplicación algebraica como si fueran polinomios, y luego hacer las sustiticiones indicadas por las ecuaciones de Hamilton:

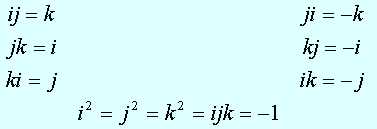
Ejemplo:

O para ser sintéticos, podemos usar la generalización de la siguiente fórmula:

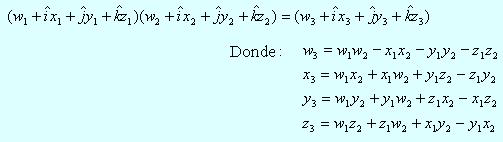
Que escrita en un formato más compacto se puede representar así:

Recordemos que los cuaternios también se pueden representar como un número de la forma (w, V), donde w es la parte real, y V es el vector que corresponde a la parte imaginaria.

Consideremos que estamos multiplicando los cuaternios (w, x, y, z) y (w', x', y', z').
Sea entonces V = [x, y, z] y V' = [x', y', z'].

Aplicando las definiciones de producto punto y producto cruz, tenemos:

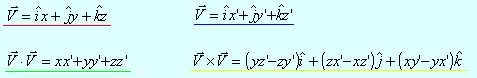
Desarrollando la multiplicación de los cuaternios:

Reagrupando los términos:

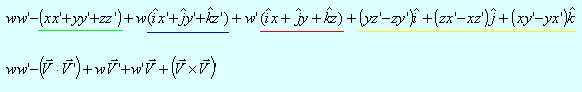
Llegamos a la forma vectorial del producto de dos cuaternios, a partir del producto punto y el producto cruz ya conocidos.

Copyright © 1999-2001 Ricardo Arturo Espinoza Reyes