Suma

+ Suma +

La suma es la operación más sencilla de definir para los cuaternios, cuando están representados en cualquier forma distinta a la polar. Si consideramos a los cuaternios:

Q = w + ix + jy + kz
Q' = w' + ix' + jy' + kz'

Su suma sería simplemente:

Q + Q' = (w + w') + i(x + x') + j(y + y') + k(z + z')

Por ejemplo:

[ 4 + 5i - 8j + 6k ] + [ 3 - 2i + 2j + k] = 7 + 3i - 6j + 7k

En las otras dos representaciones, la suma sigue el mismo principio:

La suma se efectúa como cualquier suma vectorial.

Sean A, B y C tres cuaternios cualquiera.
En general se cumple que A + B = B + A, y que A + (B + C) = (A + B) + C = A + B + C
Existe además el concepto de neutro aditivo, el cual es el cuaternio 0 + 0i + 0j + 0k, o simplemente 0.

- Resta -

Para la resta, es necesario definir primero el concepto de neutro aditivo:

Se dice que un cuaternio B es inverso aditivo de A, si se cumple que A + B = 0. Todo cuaternio tiene un inverso aditivo único, y si A es inverso aditivo de B, entonces B lo es de A.

El inverso aditivo de un cuaternio Q se representa como -Q, y equivale a sacar el inverso a cada uno de los cuatro componentes de Q. Como estos componentes son reales, y ya conocemos el concepto de inverso aditivo de un real, entonces:

Si Q = w + xi + yj + zk, tenemos que -Q = - w - xi - yj - zk.

La resta por lo tanto de A - B, equivale simplemente a la suma de A y -B.

* Conjugación *

Otra operación muy útil para los cuaternios es la conjugación. Recordemos que para un número complejo a + bi, se define su conjugado como a - bi, es decir, se cambia el signo de su parte imaginaria.

En el caso de los cuaternios, la idea es la misma, sólo que debemos cambiarle el signo a las tres componentes imaginarias. Se simboliza la conjugación con el signo * después del cuaternio. Es decir, Q* es el conjugado de Q.

Para evitar confusión con el producto, emplearé paréntesis cuando sea necesario para que no se malinterprete el operador *, por ejemplo A*B = AB, pero (A*)B = conj(A)*B.

Se cumple además que (Q*)* = Q para todo cuaternio, y que para todo número real R, ocurre que R* = R.

Estas son las definiciones de conjugado para cada representación:

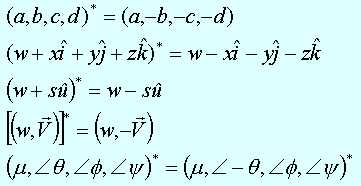
Por último, es interesante destacar que el producto QQ* es conmutativo para todo cuaternio Q, y que el resultado es siempre un real. En el apartado correspondiente a la multiplicación se analizará esto con más cuidado, pero por el momento, es útil definir: