Guitar Frequencies

Sound, Tones and Notes
 The guitar is a musical instrument, so its goal in life is to make music. Music is the arrangement of tones into patterns that the human brain finds pleasing. Let's start at the beginning with the question, "What is sound?" in order to better understand music.

Sound is any change in air pressure that our ears are able to detect and process. For our ears to detect it, a change in pressure has to be strong enough to move the eardrums in our ears. The more strongly the pressure changes, the "louder" we perceive the sound to be.

For our ears to be able to perceive a sound, the sound has to occur in a certain frequency range. For most people, the range of perceivable sounds falls between 20 hertz (oscillations per second) and 15,000 hertz (oscillations per second). We cannot hear sounds below 20 hertz and above 15,000 hertz.

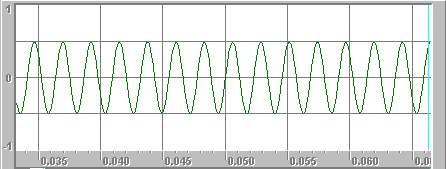
A tone is a sound that repeats at a certain, specific frequency. This 440 hertz tone can be pictured as a sine wave, like this:

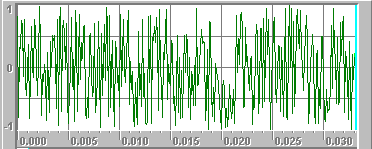
A tone is made up of one frequency or very small number of related frequencies. The alternative to a tone is a combination of hundreds or thousands of random frequencies. We refer to these random-combination sounds as noise. When you hear the sound of a river, or the sound of wind rustling through leaves, or the sound of paper tearing, or the sound made when you tune your TV to a non-existent station, you are hearing noise.

Noise sounds random and also presents itself graphically as randomness:

A musical note is a tone. However, a musical note is a tone that comes from a small collection of tones that are pleasing to the human brain when used together. For example, you might pick a set of tones at the following frequencies:

This particular collection of tones is known as the major scale. If you multiply 264 by the fraction 9/8 you get 297. If you multiply 297 by the fraction 10/9 you get 330. If you multiply 330 by the fraction 16/15 you get 352. If you multiply 352 by the fraction 9/8 you get 396. If you multiply 396 by the fraction 10/9 you get 440. If you multiply 440 by the fraction 9/8 you get 495. If you multiply 495 by the fraction 16/15 you get 528. Why are these particular fractions chosen in the major scale? Simply because they sound pleasing. Listen: These particular tones have been given letter names, and also word names, like this: The names are totally arbitrary. Same thing with the fractions - it just turns out that they have a pleasing sound to human ears.

One thing to notice is that the two C notes are separated by exactly a factor of two. 264 is one half of 528. This is the basis of octaves. Any note's frequency can be doubled to "go up an octave", and any note's frequency can be halved to "go down an octave".

You may have heard of "sharps" and "flats". Where do they come from? The scale of tones shown above is "in the key of C" because the fractions were applied with C as the starting note. If we were to start the fractions at D, with a frequency of 297, then we would be "tuned to the key of D" and the frequencies would look like this:

The notes at 297 hertz (D), 396 hertz (G) and 495 hertz (B) in the key of D match the same notes in the key of C exactly. The E note in the key of D (at 334.1 hertz) is pretty close to the E note in the key of C (330 hertz). The same applies for the A note. F and C, however, are distinct in the two keys. F and C in the key of D are therefore referred to as F# (F sharp) and C# (C sharp) in the key of C. [Note that F sharp is also known as G flat, and C sharp is known as D flat]. If you apply the fractions to several different keys, merge together all the identical and pretty-close notes, and then look at the unique sharps that fall out, you realize that you need A#, C#, D#, F# and G# to handle all the keys.

You can see that, with all of these mergings of keys, the major scale can leave you with some pretty arbitrary decisions to make when you tune an instrument. For example, you can tune the major notes to the key of C, and then the sharps for F and C to the key of D, and the sharps for D and G to..., or you could..., or.... It can get pretty messy.

Therefore, over time, most of the musical world came to agree on a scale called the tempered scale, with the A note set at 440 hertz and all of the other notes tuned off of that. In the tempered scale, all of the notes are offset by the 12th root of 2 (roughly 1.0595) instead of the fractions we saw above. That is, if you take any note's frequency and multiply it by 1.0595, you get the frequency for the next note. Here are three octaves of the tempered scale:

As you can see in this table, we have finally been able to get the discussion back to guitars! This is how a guitar is tuned. A guitar with 12 clear frets has a range of 3 octaves as shown above. The open 6th string is the lowest note and the 12th fret on the first string is the highest. Here is the actual layout of all of the notes on a guitar.

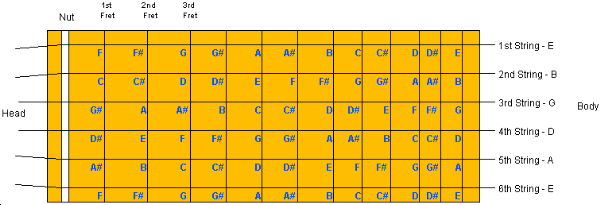
You can see in this diagram that there are 72 fret positions, but the table above shows only 37 unique notes. Therefore you have multiple ways to finger identical notes on a guitar. This fact is frequently used to get all of a guitar's strings tuned. For example, you can tune A on the first string (5th fret) to 440 hertz. Then it is a fact that E at the 5th fret on the second string is the same as the open first string, so you you match those two notes up by tuning the second string. Similarly:

Once you have all of the strings on a guitar perfectly tuned, using 440 hertz for A as the primary note, then the guitar will have notes with the frequencies shown in the table above and it is said to be tuned to "concert pitch".

[Fun fact: a piano has 88 keys stretching through more than 7 octaves. The lowest note on a piano vibrates at 27.5 hertz and the highest vibrates at 4,186 hertz.]