|
Example: Consider a continuous set of waves with l = 2 cm such that 2.5 complete waves pass by a fixed point every second. How fast is the wave travelling?
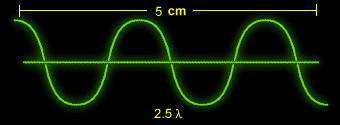
The wave traveled 5 cm in 1 second
and the frequency is 2.5 Hz.
Therefore, 5 cm/s = speed.
NOTE: 5 = 2.5 * 2 cm
Therefore,
v = f l
The Wave Equation is an expression which gives the speed of the wave. The Wave Equation is stated below:

Frequency and wave length are inversely related to each other as the two digrams below show:
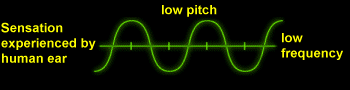
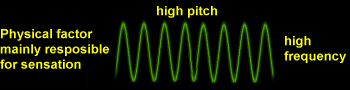
During a period the wave travels 1 l. Therefore, an alternate expression for the speed of a wave is as follows:

A standing wave interference pattern results when two sets of waves with the same amplitude and wavelength travel in opposite directions in the same medium and travel through each other.
A node or nodal point (N) is a point that remains at rest throughout the interference. The region between the nodes are areas where double crests and double troughs occur. These areas are called loops or antinodes.

1) The point X represents a point of total cancellation of a wave. The X also represents a node or nodal point.
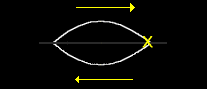
2) The point X represents a momentary cancellation of a wave.
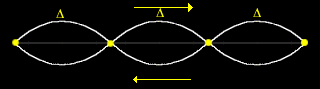
3) The dots represent nodes (stationary points) and the D are antinodes (loops).
To find the wavelength of a loop, you can see that 2 loops = l. Therefore, 1 loop = 1/2 l.
A free-end reflection has no inversion. When this occurs there is no phase change. Waves of this nature are found in open end air columns as found in brass or horn instruments such as the tromebone and trumpet.
When two or more waves act simultaneously on the same particles of a medium,
it is referred to as an interference of waves.
A constructive interference occurs when two or more waves interfere to
produce a resultant displacement greater than the displacement that would be
caused by either wave itself.
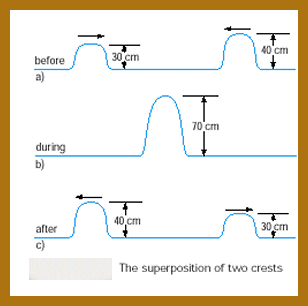

You can see that the so called superwave has an amplitude of 70 cm, the sum of both wave's amplitudes.
A destructive interference occurs when the resultant displacement is smaller than the displacement that would be caused by either wave itself.
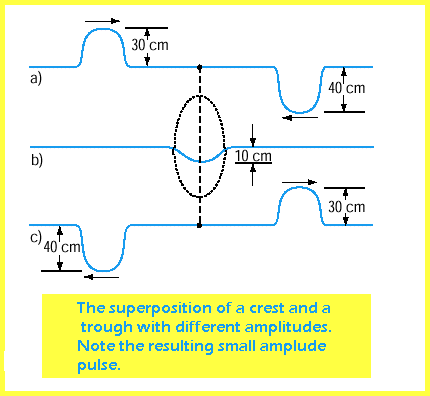
The Principle of Superposition states that the resultant displacement of a given
particle that is equal to the sum of the displacements that would have been produced
by each wave acting independently.
Note to be Made from this Section
An exercise to show this graphically is to add a sine wave to a cosine wave.
Lab Exercise
A graph is to be drawn, using a calculator to obtain the values for a sine wave from 0o to 540o. This will genetate a wave and a half.
Select a colour for this function.
On the same graph sheet sketch a cosine function from 0o to 540o. This will also produce a one and a half wavelenghts. Select another colour when drawing this function.
The two waves are to be added and the new wave (sine + cosine) is sketcked on the same graph sheet again using a different colour.
Mark areas on the diagram where maximum constructive interference and desructive interfence occurs.
BACK TO TOP