Interference of Sound Waves

Interference of Identical Sound Waves

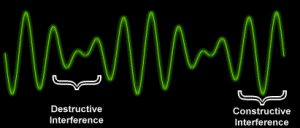
When two or more sets of sound waves pass through each other, the resulting amplitude of the vibrating air molecules is the sum of the individual waves' amplitudes (PRINCIPLE OF SUPERPOSITION)

When the resulting amplitude is small, the sound is faint, and vice versa. When the interference creates large amplitude, the sound is louder.

When the interference is destructive, compressions from one source meet rarefactions from the other source, the resulting sound is faint. When the interference is constructive, the sound is louder.

Silent Regions Around a Tuning Fork

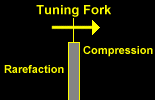
The tine emits two sets of waves with the SAME frequency. As the waves travel out, they interfere with each other. In some regions, the interference is destructive, which produces a faint sound. In other regions, the interference is constructive, resulting in a louder sound.

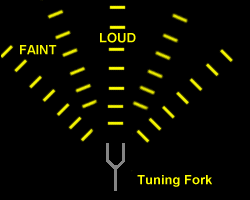
The interference pattern produced by a vibrating tuning fork.

Production of Beats

If two sets of sound waves with different frequencies interfere, they are alternately in step (sound is loud) and out of step (sound is faint). This periodic increase and decrease in loudness is called the phenomenon of beats

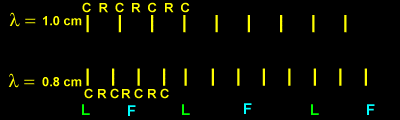
The beat frequency is equal to the difference of the two frequencies producing the beats.

Only if the beat frequency is not to high, that is the two frequencies producing them differ slightly.

 Here is an example of the Production of Beats.

Example: 130 Hz and 128 Hz or 132 Hz produce two beats per second (130 +/- 2).

Demonstration:
- Two identical tuning forks.
- One tine on one fork has a paper clip on it, this slows it down, creating beats.
- Both forks must be played at the same time in order to hear the beats.

The number of maximum intensity points that occur per second is called the beat frequency. The formula to find the beat frequency is as follows:

Note to be Made

1. Explain the difference between constructive and destructive interfence.
   Draw a digram to show each. Have the two wave to be added in different colours and the resultant wave, showing the interfence patterns in another. Digrams should be drawn as sine wave functions. Simply adding two sine waves out of sync will do the trick.
2. Explain how a tuning fork has regions of loud and very faint sound.
3. Explain how "beats" are produced.
4. Explain how listening for beats can be useful in tuning a guitar.
5. If a guitar string has a frequency of 440 Hz and is being tuned with a second string with a frequency of 442 Hz, how many beats are heard per second?
6. Two guitar strings are sounded together and 4 beats per second are heard.
   1. If one string has a frequency 196.0 Hz, what are the possible frequencies of the other string? Look ahead into the next module and label this frequency as a musical note.
   2. If the four beats heard where detected when tuning the D or 4th string to the G or 3rd string, what would you have to do to D string to bring it into tune with the G or 3rd string? Explain the two possibilities.

BACK TO TOP