Ушедший ХХ век воспринимается нами не только как век величайших научных открытий, но и как век возникновения новых инженерно-технических областей человеческой деятельности. Одной из таких областей стало создание и широкое использование квантовых приборов, способных генерировать остронаправленное когерентное почти монохроматическое электромагнитное излучение оптического диапазона длин волн. Полное наименование таких приборов звучало так: Light Amplification by Stimulated Emission of Radiation, что переводится как Усиление Света за счет Вынужденного Излучения. Для повседневного пользования название слишком длинное. Поэтому возник его короткий вариант в форме аббревиатуры: LASER. В полном названии присутствуют два ключевые понятия, определяющие физическую основу таких приборов: 1) усиление света и 2) вынужденное излучение.
Создание лазеров прямо связано с проблемой усиления света при его прохождении через специально подготовленную оптическую среду. Задача техники – обеспечить создание сред, способных усиливать проходящий через них световой луч. Научное изучение взаимодействия света с веществом продолжается на протяжении примерно 300 лет, но вплоть до рубежа XIX и XX веков изучение велось на феноменологическом уровне. А на таком уровне известен факт поглощения света, но даже не возникал вопрос о возможности его усиления. Весь опыт науки не такого уж далекого прошлого убеждал ученых, что любая оптическая среда способна только поглощать и рассеивать проходящий через нее свет.
Одним из следствий открытия в начале ХХ века микромира стало понимание природы процессов испускания и поглощения света вещественными частицами – атомами, молекулами и ионами. Для примера ограничимся представлениями об испускании и поглощении света атомами. Атом обладает определенной потенциальной энергией связи электронов с ядром. Он стремится занимать такое состояние, при котором эта потенциальная энергия минимальна. Такое состояние принято называть основным состоянием атома. В среде, содержащей большое количество атомов, протекают процессы их соударений. Большинство таких соударений происходит упруго, потенциальная энергия каждой частицы остается прежней. Реже столкновение протекает неупруго, тогда часть кинетической энергии одного из столкнувшихся атомов передается партнеру, потенциальная энергия которого после этого возрастает. Состояние такого атома называют возбужденным. Однако, в отличие от макромира, в микромире передача атому энергии извне осуществляется только строго определенными дискретными порциями. Атом данного элемента обладает системой дискретных энергетических уровней, присущей только этому элементу. На рис.1 приведена упрощенная схема энергетических уровней атома.
(1.1)Здесь n i – концентрация возбужденных атомов на i-том квантовом уровне с энергией Еi, n - общая концентрация атомов, k – постоянная Больцмана. Из этого соотношения видно, что чем выше энергия дискретного квантового уровня, тем меньше на нем концентрация возбужденных атомов, и падение их числа происходит по экспоненциальному закону.
Проходящий через оптическую среду световой луч можно рассматривать как поток фотонов, двигающихся в определенном направлении. На своем пути фотоны сталкиваются с атомами. Такие столкновения следует рассматривать как столкновения двух частиц, происходящие либо упруго, либо неупруго. В случае упругого столкновения происходит рассеяние фотона, направление его движения изменяется. С неупругими столкновениями дело обстоит сложнее.
Фотон при неупругом столкновении с определенной вероятностью может передать свою энергию атому только целиком, при этом он исчезает. Если через среду проходит монохроматичный луч света, то поглощение фотонов атомами с определенной вероятностью произойдет лишь при условии, что энергия фотона
(h- постоянная Планка,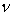 
- частота электромагнитной волны) точно равна той порции энергии, которая соответствует энергетическому переходу атома в данное возбужденное состояние, на присущий ему квантовый уровень. На рис.1 поглощение фотона изображено самой левой стрелкой. В противном случае поглощение не состоится, дело ограничится только рассеянием фотонов на атомах среды. Неупругие столкновения фотонов с атомами определяют протекание процесса поглощения света веществом. В атоме энергию поглощаемого фотона воспринимает один из внешних электронов.
Атом пребывает в возбужденном состоянии ограниченное время. Его возвращение в основное состояние может происходить в одном из трех процессов: 1) при столкновении с другим атомом (или электроном), сопровождаемым передачей ему энергии возбуждения в форме кинетической энергии движения (безизлучательный переход); 2) путем спонтанного излучения, происходящего случайным образом, когда время между возбуждением атома и испусканием фотона определяется лишь вероятностно. В среде, состоящей из большого количества возбужденных атомов, спонтанное девозбуждение сопровождается излучением фотонов разных энергий (частот), вылетающих в разных направлениях и по фазе независимо друг от друга. В качестве примера на рис.1 представлены два возможных варианта спонтанного излучения. Вторая слева стрелка изображает излучение фотона атомом, возбужденным до состояния с энергией E n, путем перехода электрона с верхнего возбужденного уровня сразу в основное состояние с энергией Е0. Уносящий энергию возбуждения фотон имеет ту же частоту, что и поглощенный фотон, но направление его движения, поляризация и фаза совсем иные, чем у поглощенного фотона. Кроме того, девозбуждение может протекать ступенчато (каскадно), как показано правой группой стрелок. Например, первоначально происходит переход электрона между верхним возбужденным уровнем и вторым уровнем схемы, тогда испускается фотон с энергией (частотой), определяемой разностью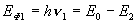 
. Затем может произойти повторный акт спонтанного излучения, определяемый переходом электрона со второго на первый энергетический уровень: 
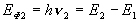. Еще один, третий переход, отмечает возможность безизлучательного возвращения атома в основное состояние, если возбуждение снимается соударением атома с частицей, которой передается вся остаточная энергия возбуждения в форме изменения кинетической энергии движения этой частицы. Понятно, что в каждом конкретном случае варианты переходов могут быть различными.
3) Кроме спонтанного существует еще один вид излучения, получивший название вынужденного излучения. Этот вид излучения был теоретически предсказан А.Эйнштейном в 1916 году и вскоре после этого получил экспериментальное подтверждение. Открытие вынужденного излучения послужило сигналом, показавшим принципиальную возможность усиления света, проходящего через оптическую среду. Если в непосредственной близости от возбужденного атома пролетает фотон, энергия (и частота) которого точно соответствует энергии перехода из возбужденного состояния в энергетически более низкое состояние, то существует вероятность того, что такой фотон заставит атом испустить квант света той же энергии (частоты) и в том же направлении, что и у фотона-инициатора. Более того, испущенный фотон будет иметь ту же поляризацию и ту же фазу, иначе говоря, это будет точный близнец первичного фотона. Говорят, что такие фотоны когерентны. В результате каждого акта вынужденного излучения число фотонов в монохроматическом луче увеличивается, таким образом, вынужденное излучение способно усиливать свет. Однако, в земных условиях никому не удавалось наблюдать увеличение интенсивности света на выходе оптической среды по сравнению с его интенсивностью на входе. Какова причина, ведь существование вынужденного излучения подтверждено экспериментально?
Дело в том, что оптические среды, в которых имеются атомы, находящиеся в возбужденном состоянии, обычно характеризуются квазиравновесностью, при которой распределение возбужденных атомов по энергетическим уровням подчиняется закону Больцмана (1). В такой ситуации господствуют процессы спонтанного девозбуждения атомов, что означает господство процессов уменьшения числа фотонов в проходящем луче. Вынужденное излучение создает лишь небольшую поправку к таким процессам. Для того, чтобы в среде господствовало вынужденное излучение, необходимо выполнение трех условий. Во-первых, в среде должно присутствовать большое количество возбужденных атомов. Во-вторых, основная масса возбужденных атомов должна занимать определенный верхний энергетический уровень, обладающий относительно большим временем жизни. В-третьих, должен существовать хотя бы один нижележащий уровень с очень коротким временем жизни, который находится в почти свободном состоянии и на который разрешен излучательный переход с верхнего заполненного уровня. Эти условия означают сильное отличие от больцмановского распределения, крайне неравновесное состояние оптической среды, получившее название инверсной населенности. Естественным путем в земных условиях такое состояние оптической среды не возникает. Но, как выяснилось, инверсную населенность можно создать искусственно, путем выбора составляющих оптическую среду элементов и направленным введением в нее энергетического потока (накачка среды).
В тридцатых годах ХХ века проблемой усиления света занялся известный физик Валентин Александрович Фабрикант. К 1948 году он вместе со своей аспиранткой Ф.А. Бутаевой создал газоразрядную установку, на которой впервые в мире осуществлено усиление проходящего через оптическую среду монохроматического светового луча. До создания лазера, способного генерировать монохроматичный узконаправленный когерентный луч, оставалось совсем немногое – создать положительную обратную оптическую связь, превращающую усилитель в генератор. Сделать такой шаг в оптическом диапазоне длин волн удалось в 1960 году Теодору Мэйману, поместившему в оптический резонатор (между двумя плоскопараллельными зеркалами) стержень из синтетического рубина, ставшего активной средой первого твердотельного лазера. Накачка рубина осуществлялась мощным импульсным световым потоком, создаваемым импульсными газоразрядными лампами. Затем появился первый газовый He-Ne лазер, а в 1964 году Кумар Н. Пател получил генерацию от первого молекулярного СО2 лазера. Далее началось бурное развитие подобных квантовых приборов, и, что особенно важно, немедленное их использование в различных научных, технических и медицинских приложениях. Типы создаваемых лазеров отличаются агрегатным состоянием активной среды, способом накачки, режимами работы, выходными характеристиками оптического луча. Физические основы лазеров подробно рассматриваются, например, в [1,2]. Создававшиеся в начальный период лазеры обладали сравнительно небольшими энергетическими и мощностными характеристиками. Возникла серьезная проблема повышения энергетики некоторых таких лазеров, что позволило бы использовать их для так называемой «силовой» обработки материалов – резания, сварки, обработки поверхностей и т.д. Этой проблеме и посвящена данная книга.
Термин «мощные лазеры» имеет однозначный смысл, когда речь идет о лазерах, работающих в режиме непрерывной генерации. В этом случае повышение мощности сопровождается повышением энергии излучения, выделяемой в единицу времени, и, соответственно, повышением активности процесса взаимодействия лазерного излучения с веществом. Поэтому можно условиться о проведении некоей границы мощности, превышение которой отнести к категории мощного излучения. Например, таким рубежом можно назвать мощность излучения в 1 кВт, а можно предложить считать рубежом мощность в 100 Вт. Выбор условной границы, отделяющей «мощные» лазеры от «не-мощных», определяется конкретными задачами применения лазеров, когда необходимо превысить определенные пороговые уровни термических и иных воздействий лазерного излучения на материалы.
Но этот же термин приобретает неопределенный смысл, когда лазер генерирует излучение в импульсном или частотно-импульсном (его также называют импульсно-периодическим) режимах. Одиночный импульс характеризуется несколькими значениями мощности. Во-первых, существует мгновенное значение мощности (мгновенная мощность): при общей длительности импульса tи в любой момент времени ti в интервале 0< ti < tи выделяется малый временной интервал 
t I , в котором можно пренебречь изменением величины мощности.
Мощность, выделяющуюся в этом временном интервале, и называют мгновенным значением для момента времени tI . Если все мгновенные значения мощности на протяжении импульса соединить плавной кривой, как это сделано на графике рис.1.2, то эта кривая даст представление о форме импульса мощности лазера.
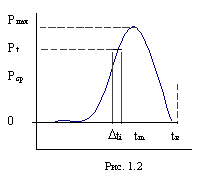
Именно такую кривую мы увидим на экране осциллографа, на вход которого подается сигнал от регистратора мощности с высоким временным разрешением. На графике мгновенная мощность обозначена символом Pt.
Далее, в момент времени tmax достигается максимальная за импульс мгновенная мощность
Pmax . Ее называют пиковой мощностью. Площадь, ограниченная осью времени и кривой мощности,
пропорциональна энергии лазерного импульса Е. Разделив энергию на длительность
импульса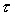 
, получим среднее за импульс значение мощности: 
.
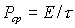Ее называют средней мощностью. При одном и том же значении энергии в импульсе средняя мощность
зависит от длительности импульса. Например, лазер генерирует малую энергию в импульсе, порядка 0,1 Дж.
При миллисекундной длительности импульса (это характерная длительность генерации неодимового лазера,
10-3 – 10-2 с) средняя мощность составит 10 - 100 Вт. В микросекундном диапазоне
(СО2 лазер, 10 -6 - 10-5 с) она достигнет 105 – 104 Вт.
В наносекундном диапазоне (модуляция добротности у твердотельного лазера 10-9 - 10-7 с)
это будет гигантская мощность 108 – 106 Вт и окажется еще более высокой у лазеров,
генерирующих импульсы в пикосекундном (10-12 – 10-10 с)
диапазоне – от 1011 до 109 Вт. И все это при той же незначительной энергии в импульсе.
Из приведенных оценок видно, что энергетически маломощный лазер с очень коротким импульсом обладает фантастически высокой мощностью. Но нас в дальнейшем будут интересовать лазеры, способные эффективно воздействовать на материалы, а такие лазеры должны обладать достаточно высокой энергией в импульсе. В этом случае высокий уровень мощности сам по себе не является привлекательным. Поэтому условимся считать мощными лазерами те из них, которые наряду с высокой средней мощностью обладают и высокими значениями энергии в импульсе.
При рассмотрении частотно-импульсного режима работы лазера, к характеристикам отдельного импульса добавляется еще одна мощностная характеристика – средняя мощность последовательности импульсов. Это эквивалент энергетического потенциала лазера, но при условии, что дополнительно сообщаются данные об энергии в каждом импульсе, а также данные о длительности и частоте следования импульсов (или о скважности).
Итак, термин «мощный лазер» мы сохраним в его оговоренном выше значении, и будем под ним понимать только те лазеры, которые генерируют мощное высокоэнергетичное излучение.
Интерес к мощным лазерам определяется их способностью оказывать тепловое воздействие на различные материалы в условиях, когда излучение концентрируется в малоразмерное пятно. Соответственно появляются возможности различных приложений таких лазеров, в том числе и в качестве инструмента для технологической обработки материалов. Имеются в виду процессы резания и сваривания металлов и неметаллов, точного пробивания отверстий (сверление), термического упрочения поверхностей (закалка) и их очистки, нанесения маркировочных знаков, гравировка. Мощные лазеры внедряются в такие сферы промышленного производства как автомобилестроение, судостроение, авиационное и космическое производство, производство крупных установок для добычи нефти и газов и в некоторые другие области. В конце 80-х, начале 90-х годов лидером по внедрению лазерных технологий в промышленность являлась Япония, за ней следовали США и европейские страны, среди которых первенство принадлежало Германии.
Лазерные технологии не вытесняют традиционные способы обработки материалов, они сосуществуют с ними, занимая те «экологические» ниши, в которых оказываются более выгодными, более производительными и экономически оправданными. Надо помнить, что стоимость лазерного оборудования и его эксплуатации, как правило, существенно выше, чем стоимость хороших механических, ультразвуковых и даже плазменных обрабатывающих станков. Но в определенных случаях только лазерный луч оказывается способным выполнить ряд технологических операций, необходимых для изготовления наукоемких изделий и тогда вопросы стоимости перестают играть ведущую роль.
Назову некоторые особые области применения мощных лазеров: в медицине для проведения некоторых сложных операций применяют лазерные скальпели; мощные лазерные лидары используются для дистанционного обнаружения опасных с экологической точки зрения выбросов или наличия в атмосфере распыленных отравляющих веществ; известны многочисленные военные приложения таких лазеров; рассматриваются проекты по осуществлению передачи лучистой энергии с Земли на космические станции и, наоборот, из космоса на Землю; путем лазерного облучения намереваются осуществлять коррекцию орбит околоземных спутников и т.д. Важную роль выполняют мощные лазеры в научных исследованиях по проведению управляемого термоядерного синтеза, при исследованиях взаимодействия мощного излучения с веществом. Но сегодня только лазерная промышленная технология пользуется заметным международным спросом.
Существующее разнообразие типов лазеров вызывает необходимость их классификации. Прежде всего, лазеры различают по агрегатному состоянию активной среды, разделяя их на твердотельные (в этой группе отдельно рассматривают полупроводниковые лазеры), жидкостные и газовые. Далее, лазеры подразделяются на группы по способу накачки: существует оптическая накачка, электрическая и электроразрядная накачки, химическая накачка и накачка с использованием потоков заряженных микрочастиц, прежде всего электронов. Далее, различают лазеры по режиму их функционирования: используется три таких режима – импульсный, частотно-импульсный и непрерывный.
Далеко не все типы лазеров в принципе способны генерировать мощное высокоэнергетичное излучение. В данной книге я ограничусь рассмотрением только двух разновидностей лазеров, которые широко применяются сегодня в технологических процессах обработки материалов и в научных исследованиях взаимодействия лазерного излучения с веществом. Это, прежде всего СО2 лазеры, активная газовая среда у которых состоит из определенной смеси газов, где главную роль играют молекулы двууглекислого газа. Накачка таких лазеров производится с помощью электрического разряда в газе или комбинированным способом, когда к разряду добавляется поток быстрых электронов. СО2 лазеры способны работать во всех ранее перечисленных режимах генерации – в импульсном, частотно-импульсном и непрерывном.
Второй тип лазеров, подлежащий рассмотрению – твердотельные лазеры на стеклах с присадкой неодима или на алюмоиттриевом гранате с присадкой того же неодима (YAG: Nd). Накачка этих лазеров осуществляется оптическим путем с использованием высокоинтенсивных импульсных источников света. Лазеры со стеклами в качестве активной среды работают только в импульсном режиме генерации, а YAG обеспечивает возможность получения генерации и в частотно-импульсном режиме с частотами не выше нескольких десятков герц.
Мощное лазерное излучение может быть получено и в некоторых других лазерных системах. Например, созданы мощные химические лазеры, использующие в активной среде соединения DF и HF. Они генерируют излучение в инфракрасной области спектра на длинах волн 3-4 мкм с мощностью до нескольких сотен кВт. Большие энергии в импульсе получены в так называемых лазерах с взрывной накачкой – до 1 МДж. Внушительные энергии в импульсе при очень короткой их длительности получены с фотодиссоционными лазерами. Но все эти системы не пригодны в производственных условиях для проведения технологических операций, поэтому их рассмотрение в книге исключается.
В заключение остается уточнить понятие «техники мощных лазеров». Предполагается, что читатель, в общем, знаком с принципами функционирования лазеров, с оптическими резонаторами и основными особенностями источников электропитания. По этим разделам техники имеется большое число хороших учебных книг, к которым при необходимости читатель сможет обратиться. В данной книге речь пойдет о конкретных технических средствах, обеспечивающих реализацию больших мощностей и энергий в установках двух обозначенных выше типов лазеров. Однако технические решения проблемы создания мощного лазера невозможно получить без понимания физических принципов работы каждого конкретного устройства. Поэтому физические аспекты будут нами рассматриваться в тесной связи с особенностями рассматриваемого лазера.
Вместе с тем важно понять, каким образом высокоэнергетичное лазерное излучение может быть использовано в качестве инструмента для так называемой «силовой» обработки конструктивных материалов. Рассмотрению этой проблемы будет посвящен четвертый раздел книги, в котором приводятся экспериментальные результаты исследования условий, обеспечивающих проведение силовых технологических процессов и используемых для этого лазерных станков.
По введенной классификации СО2 лазеры – молекулярные газовые лазеры с накачкой электрическим разрядом, способные работать в любом из трех указанных режимах – непрерывном, импульсном и частотно-импульсном. Активная среда таких лазеров представляет собой смесь газов, принципиально важными компонентами которой служат молекулы СО2 и азота N2 . Лазерный эффект обеспечивается молекулами двуокиси углерода, а удивительные свойства молекул азота, как будет показано дальше, позволяют эффективного задействовать молекулы СО2 в электрическом разряде, обеспечивающим накачку лазерной среды. Электрический разряд создает плазму, которая и является активной лазерной средой. Существуют разные типы электрических разрядов, но не каждый из них пригоден для создания активной среды СО2 лазера. Для понимания принципов работы СО2 лазера и возможности получения высоких мощностей и энергий генерируемого излучения, необходимо ознакомиться с кратким обзором физики электрического разряда в газах и со свойствами плазмы, при которых возможна накачка активной среды. Для такого знакомства существуют курсы физики газоразрядной плазмы, например, [3-6]. В предлагаемом кратком обзоре приводятся самые необходимые сведения из этой области науки, необходимые для понимания дальнейшего изложения темы.
На Земле природные плазменные образования встречаются не часто. Поэтому знакомство человечества с плазменным состоянием вещества началось сравнительно поздно, примерно с середины XIX века. Толчком к формированию физики плазмы как научной дисциплины послужили два обстоятельства. Во-первых, внедрение в астрономию физических методов дистанционного изучения космических объектов, находящихся в состоянии плазмы и излучающих электромагнитные волны. Это звезды, многие туманности и другие объекты. Было установлено, что 99,9% вещества во Вселенной находится в состоянии плазмы, а Земля – это малое исключение из общего правила. Началось активное изучение процессов, приводящих к образованию плазмы, и процессов, протекающих в самой плазме. Во-вторых, с началом широкого внедрения электричества в повседневную жизнь людей появились возможности создания бытовых и промышленных устройств, генерирующих и использующих плазму. Началось интенсивное экспериментальное исследование плазмы и разработка ее теоретических основ.
Термин «плазма» введен в обращение в 1924 году Тонгсом и Ленгмюром – двумя выдающимися физиками, много сделавшими в сфере, как экспериментального изучения плазмы, так и создания теоретических основ.
Определение: плазма – квазинейтральная система, содержащая смесь заряженных и, возможно, нейтральных частиц вещества.
Требование квазинейтральности – важнейшее условие, включенное в определение плазмы. Из него вытекают три ключевые следствия:
- в плазме содержатся равные количества положительно и отрицательно заряженных частиц;
- заряженные частицы образуют однородную смесь, так что плазменный объем нейтрален не только в целом, но и в каждой своей не слишком мелкой части;
- плазма является макрообъектом, содержащим большое количество заряженных частиц в своем объеме, а время существования плазменного состояния не может быть сколь угодно малым.
Рассмотрим эти три следствия подробнее. Создающие плазму заряженные частицы образуются в процессе объемной ионизации газа, при протекании которого всегда возникают равные количества положительно (ионы) и отрицательно (электроны) заряженных частиц. Важной характеристикой плазмы служит степень ее ионизации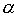 
. Это отношение концентрации электронов ne к концентрации всех тяжелых частиц в среде, то есть к сумме концентраций нейтральных частиц na и ионов ni:
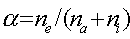
(2.1) Если 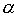< 1 (не все атомы или молекулы ионизованы), то плазму называют частично ионизованной. При 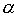= 1 плазма полностью ионизованная (однократно). Наконец, если 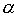> 1, то это характеризует двукратно или многократно ионизованную плазму.
Второе следствие становится понятным, если мы рассмотрим ситуацию, когда из-за случайных причин возникает локальное временное разделение заряженных частиц разных знаков. Такое разделение нарушает нейтральность плазмы. Допустим, возникла ситуация, когда в одной локальной области, присутствует избыточное количество положительно заряженных ионов, а в другой – такое же по количеству избыточное содержание электронов. Возникает кулоновское взаимодействие разноименных зарядов, и электроны, как более легкие частицы, устремляются к объему с избыточными ионами. По инерции они проскакивают через этот объем, затем тормозятся и устремляются в обратном направлении и так далее. Возникают плазменные колебания, происходящие с частотой, согласно расчетам определяемой соотношением (2.2):
(2.2) где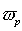 
– в с–1, а ne – в см– 3.
Такие плазменные колебания теоретически предсказал, а затем и экспериментально обнаружил Ленгмюр. Поэтому у них появилось второе название – ленгмюровские колебания. Зная частоту плазменных колебаний, можно определить то минимальное время, которое служит нижним временным пределом существования квазинейтральности. Этот нижний предел определяется временем, в течение которого локальные нарушения квазинейтральности из-за случайного разделения зарядов четко себя проявляют, то есть оно должно быть того же порядка, что и период плазменных колебаний. Если время существования плазмы охватывает несколько периодов ленгмюровских колебаний, то картина усредняется и среда предстает как квазинейтральная. Время tD, меньше которого ионизованный газ проявляет локальное отклонение от квазинейтральности, что не позволяет называть его плазмой, это – временной масштаб, отделяющий продолжительность существования просто ионизованного газа при слишком коротком времени его существования от состояния плазмы, возникающего при более продолжительном существовании ионизованной среды:
(2.3)Пример: концентрация заряженных частиц в ионизованном газе равна ~1012 см–3. Из соотношения (2.3) определяем, что tD ~ 6.10-11 c. Это очень маленькое время, но оно имеет место в импульсах длительностью порядка пикосекунд. Если мы попытаемся образовать плазму с таким временем существования, то даже при столь относительно низкой концентрации электронов, как в данном примере, в лучшем случае возникнет ионизованный газ, по определению не удовлетворяющий понятию плазма. С повышением концентрации электронов временной масштаб укорачивается, и шансы создать плазму с очень коротким временем жизни резко снижаются.
Но локальное нарушение квазинейтральности может происходить не только при очень коротких временах существования ионизованного газа, но и при очень малых объемах, выделяемых нами для рассмотрения деталей. Отсюда появляется еще один критерий существования плазмы, который называют пространственным масштабом.. Пространственное разделение зарядов определяется из условия, что энергия теплового движения заряженных частиц, способная вызвать такое разделение, не превышает энергии кулоновского взаимодействия между ними, препятствующего разделению. Энергия теплового движения частиц характеризуется температурой, она равна kТ, где k – постоянная Больцмана (k = 1,39.10-16 эрг/К =1,39.10-23 Дж/К). Энергия кулоновского взаимодействия между зарядами: 4пne e2 ( lD ) 2, где lD – характерный минимальный размер области, всегда остающейся квазинейтральной при данных значениях тепловой и кулоновской энергий. Этот размер называют дебаевской длиной. Он же и служит пространственным масштабом существования плазмы. Из условия равенства тепловой и кулоновской энергий определяют границу минимальной области, в которой плазма уже существовать не может (дебаевскую длину):
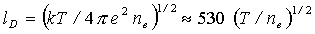
(2.4)Здесь Т – в эВ (1эВ = 11600 К), ne – в см–3.
Пример: Температура плазмы Т = 2 эВ (~23000 К) концентрация электронов ne = 1012 см-3. При этих условиях lD = 7.10- 4см.
В плане практических приложений теория плазмы должна обеспечить возможность расчетного определения параметров и свойств конкретного плазменного образования в зависимости от условий ее возникновения и существования. Теория строится на основе представлений о процессах, протекающих в плазме, что позволяет создать исходную модель и ее математическое отображение. Область применения теории ограничивается областью, в которой справедлива исходная модель.
Заряженные и нейтральные частицы, образующие плазму, обладают определенной кинетической энергией (тепловое движение), а между заряженными частицами действуют мощные кулоновские силы притяжения и отталкивания. Рассмотрение процессов, протекающих в огромной массе взаимодействующих частиц, возможно только статистическими методами. Если такой подход удается осуществить, то из исходного хаоса получают макропараметры среды, функционально зависящие от ее состояния: это температура, давление, теплопроводность, теплоемкость, электропроводность, вязкость.
Вполне удовлетворительная статистическая теория разработана для случая неионизованного газа, она известна под названием кинетической теории газов и опирается на модель парных соударений частиц. Исходная посылка кинетической теории: силы взаимодействия между микрочастицами любого сорта являются короткодействующими. Поэтому вне тесного сближения двух частиц они движутся свободно, не испытывая взаимных влияний. Такое движение характеризуется следующими величинами:
- импульсом 
, где 
– скорость, а 
– масса частицы;
- кинетической энергией; 
- внутренней энергией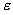 
, определяющей состояние частицы.
При тесном сближении двух частиц они начинают взаимодействовать. Каждая частица рассматривается как центр, создающий силовое поле, потенциал которого U(r) зависит от расстояния. Очень быстрое (экспоненциальное) уменьшение потенциала с расстоянием объясняет его короткодействие. Продолжительность взаимодействия двух частиц много меньше времени их свободного движения. Tакой тип взаимодействия называют столкновением частиц. А так как вероятность тройных соударений много меньше вероятности парных, то модель рассматривает все столкновения как парные.
При парном столкновении соблюдаются законы сохранения импульса и энергии. Допустим, частица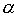
сталкивается с частицей 
. Общий импульс сталкивающихся частиц:
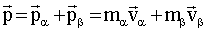
(2.5)
Обозначим через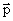 
импульс системы до столкновения, а через 
– после столкновения. Тогда, как бы не изменялись импульсы каждой из частиц в результате столкновения, общий импульс системы не изменится.
Закон сохранения энергии запишем так:
(2.6) где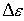 
- суммарное изменение внутренней энергии частиц в результате столкновения, 
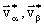– скорости частиц после столкновения.
В зависимости от характера изменения внутренней энергии различают три варианта соударений частиц:
1-ый случай. Внутренняя энергия сталкивающихся частиц не изменяется,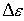
= 0. Такое соударение называют упругим.
2-й случай. Часть внутренней энергии системы превратилась в кинетическую энергию движения частиц, 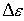> 0. Пример: столкновение электрона с возбужденным атомом, в результате которого энергия возбуждения перешла к электрону, увеличившему скорость своего движения. Это - неупругое соударение 1-го рода.
3-й случай. Часть кинетической энергии сталкивающихся частиц перешла в потенциальную энергию одной из частиц,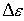
< 0. Пример: электрон при столкновении с атомом передает часть своей кинетической энергии атому и возбуждает или ионизует его. Это – неупругое соударение 2-го рода.
Предсказать движение каждой отдельной частицы в объеме, заполненном множеством таких частиц, невозможно. Однако модель парных соударений позволяет выявить в таком хаотическом движении частиц статистический порядок. Порядок определяется возникновением предсказуемого распределения частиц данного сорта по скоростям и энергиям. Распределение описывается скалярной функцией F(
), называемой функцией распределения. Здесь вектор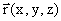 
определяет положение выделяемого для рассмотрения участка объема, вектор 
определяет интервал скоростей частиц в данном объеме. Оба вектора в совокупности определяют шестимерное фазовое пространство, и функция задает концентрацию частиц определенного сорта в единице объема этого пространства. Можно сказать и так, что функция распределения F определяет зависящую от времени плотность частиц в каждом элементе объема d3 r, скорости, которых лежат в данном интервале значений d3 v c центром в точке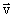 
. Несколько позже мы вернемся к рассмотрению особенностей функции распределения и ее роли в статистическом описании макропараметров изучаемой системы, таких как температура, давление, теплопроводность, вязкость и некоторые другие.
Плазма отличается от газа наличием в ней заряженных частиц, которым присущ иной вид взаимодействия – кулоновское взаимодействие зарядов. Это дальнодействующее взаимодействие, при котором одна заряженная частица взаимодействует сразу со многими другими заряженными частицами, и говорить о парных взаимодействиях частиц в этом случае невозможно. Но хотя модель парных столкновений в принципе не применима к газу, находящемуся в состоянии плазмы, в частных случаях возможен компромисс. Например, если концентрация заряженных частиц в газе при большой энергии их теплового движения (высокой температуре) относительно мала, то кулоновские силы проявляют себя умеренно, и их удается свести к эквивалентным парным соударениям между частицами, распространив на такую плазму результаты кинетической теории нейтрального газа. Критерием возможности такого приложения кинетической теории служит понятие идеальной плазмы.
Условие идеальности: число частиц в сфере дебаевского радиуса должно быть большим, 
>> 1.
Изолированный электрический заряд, плотность которого равна q, создает в свободном пространстве поле, потенциал которого меняется с расстоянием r по закону q/r. Если же заряд помещен в плазму, то возникает эффект его экранировки другими зарядами. В 1923 году Дебаем и Хюккелем было получено математическое решение задачи об экранировке зарядов в объеме. В области, окружающей ион или электрон, потенциал электрического поля меняется с расстоянием по закону:
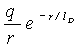
(2.8) Следовательно, влияние заряда на другие заряды уменьшается с расстоянием столь быстро, что это уменьшение можно трактовать как экранировку заряда. Поле сходит на-нет на расстоянии
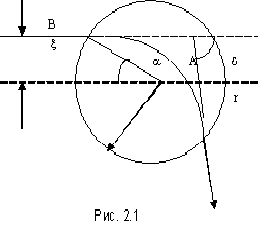
(2.9) называемом радиусом экранировки или дебаевским радиусом.
Соотношение (2.9) с точностью до множителя 2 совпадает с пространственным масштабом квазинейтральной плазмы (2.4). Условие идеальности в уточненном виде запишется так:
(2.10) Т – в эВ, ne – в см–3. Условие идеальности выполняется тем лучше, чем выше температура и чем меньше концентрация электронов в плазме.
~ 35. Концентрация частиц в дебаевской сфере достаточно велика, чтобы плазму в таком лазере считать идеальной.
В случае идеальной плазмы коллективные кулоновские взаимодействия удается представить как некие эквивалентные парные соударения, благодаря чему кинетические уравнения в несколько измененной форме (в форме уравнения Фоккера – Планка) можно использовать для описания процессов в плазме, получения функции распределения частиц в ней и нахождения интересующих нас ее характеристик.
Низкотемпературной плазмой называют среду, температура которой не превышает примерно 50 000 К. Она представляет собой смесь частиц шести типов: 1) электроны; 2) фотоны; 3) атомы (молекулы) в основном состоянии; 4) атомы (молекулы) в возбужденном состоянии; 5) положительно заряженные ионы; 6) отрицательно заряженные ионы.
Совокупность частиц одного типа принято считать одним из «газов» в смеси «газов», образующих плазму. Частицы газа вступают в «реакции» при встрече с частицами другого газа, в результате происходит «разложение» или соединение частиц, их переход из одной группы в другую. Усреднение результатов взаимодействия по большому числу столкновений позволяет определить общее состояние плазмы и характеризующие это состояние макроскопические параметры, если известны кинетические характеристики микрочастиц. Важнейшей такой характеристикой служит функция распределения частиц по скоростям или по энергиям.
Рассмотрим процесс столкновения двух выделенных частиц, например, электрона и атома. Атом рассматривается как силовой центр, создающий короткодействующую силу, способную оказать воздействие на электрон, если он попадет в сферу действия потенциала. Принято считать радиус действия силового потенциала эффективным радиусом самой частицы, в данном случае атома, по отношению к налетающей на нее частицы (электрона). Когда речь идет о среде с большим количеством взаимодействующих в ней частиц, то вводят понятие эффективного сечения столкновения, им характеризуется вероятность свершения индивидуального акта взаимодействия. В случае упругого соударения, когда эффективные радиусы сталкивающихся частиц равны соответственно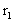 
и 
, эффективное сечение для них равно:
Но если одну из частиц можно считать точечной, то есть 
, то 
.
Обозначим эффективный радиус атома А через ra . На атом налетает электрон В согласно схеме, изображенной на рис. 2.1. Сфера с центром в точке А – это радиус действия силового потенциала атома или его эффективный радиус. Слева от сферы изображена траектория электрона до столкновения. Расстояние этой траектории от оси, проходящей через центр сферы и направленной параллельно трассе электрона, называют прицельным расстоянием, обозначим его буквой 
(кси). В результате столкновения изменяется траектория движения электрона, и угол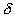 
между направлениями траектории до и после столкновения называют углом рассеяния электрона на силовом центре А. Этот угол представляется как однозначная функция прицельного расстояния. При лобовом столкновении, когда = 0, угол =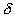 
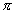и имеет место полное отражение электрона в переднюю полусферу, то есть в направлении, обратном его исходному движению. С ростом
угол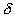 
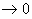. Для случая малых углов рассеяния потенциал U(r) много меньше кинетической энергии налетающей частицы К, и тогда справедливо соотношение:
(2.11) В зависимости от прицельного расстояния различают близкие и дальние столкновения. Граница между ними – прицельное расстояние, при котором угол 
, то есть тот угол, при котором отражение частиц в переднюю полусферу (близкие столкновения) сменяется их рассеянием в заднюю полусферу (дальние столкновения). Наличие большого числа частиц в плазме требует разработки статистического подхода к рассмотрению процессов их взаимодействия.
В настоящее время отсутствует общая теория коллективных взаимодействий частиц в плазме. Но в частном случае идеальной плазмы удается свести коллективные взаимодействия заряженных частиц к эквивалентным парным соударениям, что позволяет распространить в таких случаях на плазму результаты, полученные в кинетической теории нейтрального газа. Такая возможность связана с существованием эффекта экранировки зарядов. В результате экранировки возникают нейтральные группы разноименно заряженных частиц, а размер каждой такой группы определяется дебаевской длиной экранировки lD. В случае идеальной плазмы в дебаевской сфере содержится относительно большое число частиц при сравнительно малом радиусе самой сферы. Это позволяет рассматривать подобную сферу как эквивалентную нейтральную частицу, взаимодействующую с другими частицами в форме парных соударений.
По аналогии с кинетической теорией парные столкновения могут происходить либо упруго, либо неупруго. Подробности такого рассмотрения плазменных процессов представлены в [3,4]. Здесь я ограничусь схематическим изложением основных результатов такого рассмотрения.
Упругие соударения заряженных частиц. При отсутствии экранировки потенциал взаимодействия изолированных заряженных частиц равен:
(2.12)
где Z1 – заряд иона,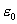 
– диэлектрическая проницаемость вакуума. В классическом приближении при таком значении потенциала взаимодействия угол рассеяния 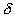связан с прицельным параметром (рис. 2.1) соотношением:
(2.13)
Здесь Z1, Z2 – заряды каждой из сталкивающихся частиц, v o - их относительная скорость,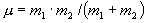 
- приведенная масса. Если одна из частиц – электрон, то 
.
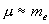Необходимо учесть неодинаковость вкладов ближних и дальних кулоновских взаимодействий. Ближние взаимодействия сопровождаются рассеянием на углы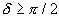 
, вероятность таких столкновений очень маленькая по сравнению с вероятностью дальних столкновений, при которых 
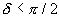. Из (2.13) следует, что при 
граничное значение 
, разделяющее ближние и дальние взаимодействия, равно:
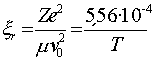
(2.14) (Т выражена в К).
В идеальной плазме рассеяние частиц на большой угол при одном столкновении внутри сферы дебаевского радиуса значительно менее вероятно, чем результирующее отклонение на большой угол в результате серии столкновений, в каждом из которых рассеяние происходит на малый угол. Для среднеквадратичного отклонения значение угла рассеяния пробной частицы (электрона), проникающей в плазму на глубину L, определяется соотношением:
(2.15) потенциал в этом случае можно представить таким:
Если кулоновский потенциал выражается в форме (2.12), то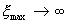 
и интеграл в (2.15) расходится. Однако учет экранировки позволяет упразднить расходимость, Тогда
(2.16) Численный коэффициент в правой части справедлив, если температура Т выражена в К. Что же касается параметра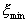 
, то учет только дальних соударений позволяет считать его равным граничному значению .
Обозначим отношение 
.
Тогда
(2.17) (Т – в К, ne - см-3).
Таким образом, если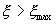 
= lD, то потенциал кулоновского взаимодействия заряженной неподвижной частицы в плазме равен нулю и налетающая частица не рассеивается. Если же 
, при условии, что в сфере дебаевского радиуса n D >> 1, попадающая в эту сферу подвижная частица будет испытывать множество дальних столкновений и по выходе из сферы она отклонится на некоторый суммарный угол рассеяния .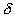
В классической теории дифференциальное сечение электрон-ионного взаимодействия определяется формулой Резерфорда:
(2.18) Формула остается без изменения и при квантовомеханическом выводе. В прикладных задачах, к которым относится и рассматриваемая нами задача о процессах газоразрядной накачки СО2 лазера, интегральным следствием парных соударений считается общее число рассеянных налетающих частиц в единицу времени независимо от угла рассеяния. Тогда долю рассеянных в потоке частиц определяют через понятие полного сечения рассеяния, которое называют транспортным сечением. Транспортное сечение, получаемое с учетом потенциала экранировки и различия удельного вклада близких и дальних столкновений, для электрон-ионных столкновений дается соотношением:
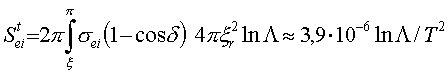
(2.19) Логарифм 
назван кулоновским логарифмом. Соотношение (2.19) справедливо в случае идеальной плазмы. Тогда оно дополняется еще двумя соотношениями, определяющими транспортные сечения электрон-электронных и ион-ионных столкновений:
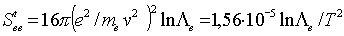
(2.19a)
(2.19b) Здесь Т – в К, ne – в см-3 , v – в cм/c.
Знание транспортного сечения позволяет определить следующие характеристики плазмы:
Частоту кулоновских столкновений:
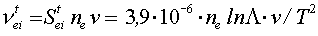
(2.20) Среднее время между столкновениями:
(2.21) Длину свободного пробега:
(2.22) Конкретные расчеты, позволяющие определить из соотношений теории столкновений частиц основные макроскопические характеристики системы, проделываются по одному из двух возможных вариантов.
Первый вариант. Функция распределения частиц по скоростям известна. Тогда транспортные сечения усредняются по функции распределения и вводятся понятия средней скорости и среднего сечения взаимодействия частиц. На их основе рассчитываются переносные коэффициенты – теплопроводность, электропроводность, вязкость, диффузия.
Второй вариант. Функция распределения неизвестна. Ее определение может быть получено решением интегро-дифференциального кинетического уравнения Фоккера-Вульфа, что представляет собой весьма непростую задачу [4].
Неупругие соударения. Наиболее значимые процессы, осуществляющиеся при неупругих соударениях: возбуждение, ионизация атомов (молекул) и обратные им процессы ударной дезактивации и рекомбинации. Коротко остановимся на этих процессах.
Возбуждение атомов электронными ударами. Неупругое столкновение свободного электрона с атомом может привести к передаче части кинетической энергии электрона атому с переводом его из основного в возбужденное состояние. Для возбуждения атома как минимум нужна энергия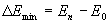 
, где Еn , Eo соответственно энергии верхнего и основного уровней перехода. Обычно эта величина составляет несколько эВ. Участвующий в столкновении свободный электрон должен обладать кинетической энергией, превышающей этот порог возбуждения. Но обладания кинетической энергией, превышающей порог возбуждения, еще недостаточно для реализации такого процесса. Существует вероятность того, что при столкновении произойдет именно акт возбуждения атома, а не рассеяние налетевшего электрона. Эту вероятность называют сечением возбуждения. Расчет сечения возбуждения сложен и чаще его величину определяют экспериментально. Она является функцией энергии налетающего электрона Ке . Например, в частном случае (для атомов ксенона и аргона) функции возбуждения представлены на рис. 2.2.
Ионизация атомов электронными ударами. Ионизация – предельный случай возбуждения, когда энергия, передаваемая электроном атому, превышает предельное значение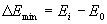 
, при котором атомное ядро еще способно удерживать около себя электрон в связанном состоянии. Ионизация не требует точной дозировки передаваемой атому энергии, так как любое превышение энергии ионизации передается освободившемуся электрону в форме кинетической энергии его дальнейшего движения.
Детальное рассмотрение процесса ионизации позволяет выделить в нем дополнительные черты. Так, первичный электрон, вызвавший ионизацию, смещает атомные электроны относительно ядра. В результате у атома появляется индуцируемый электрический дипольный момент (поляризация). Степень поляризации тем выше, чем выше атомный номер, она также сильно зависит от скорости (энергии) первичного электрона. Подобные эффекты усложняют проведение расчета энергии и вероятности ионизации атома, обе эти величины предпочитают определять экспериментально. В таблице 2.1 приводятся первые ионизационные потенциалы некоторых атомов и молекул, которые могут нам понадобиться впоследствии.
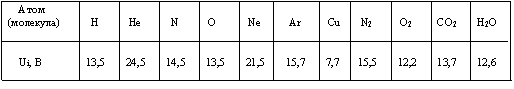
Параметр, определяющий вероятность процесса, называют сечением фотовозбуждения или сечением фотоионизации.
Термодинамическое равновесие считается одним из возможных состояний макровещества, в том числе и плазмы. Состояние системы, находящейся в термодинамическом равновесии (ТДР), можно описать как функцию двух термодинамических параметров, например, температуры и давления. В частности, для описания макроскопических параметров системы (тепловых, электрических, оптических) нет надобности привлекать к рассмотрению модель микропроцессов, это можно сделать феноменологическим подходом.
Понятие ТДР внедрилось в науку в XIX веке вместе со сформировавшейся тогда же новой научной дисциплиной – классической термодинамикой. Термодинамика обобщает накопленный человечеством опыт по изучению процессов преобразования одних видов энергии в другие, сопровождаемые совершением работы, прежде всего преобразования тепловой энергии в механическую и наоборот, а также всех остальных видов энергии в тепловую. Но предполагается, что протекание этих процессов происходит в замкнутых системах, которые не обмениваются ни энергией, ни веществом с окружающей средой. К тому же эти системы предполагаются либо равновесными, либо находящимися в состоянии, близком к равновесию.
В основе термодинамики лежит небольшое число исходных обобщений опытных данных, сформулированных в форме четырех законов или, следуя исторической традиции, четырех начал термодинамики. Представления о ТДР вытекают из второго начала, определяющего необратимую направленность любых процессов преобразования энергии в замкнутых системах. Уточним содержание терминов, которые используются нами, но о смысле которых иногда забывают.
Энергия. Смысл этого понятия до конца не прояснен, одно из принятых определений таково: это общая количественная мера движения и взаимодействия всех видов материи. Тем не менее, из этого понятия следуют вполне реальные следствия, широко используемые на практике. Например, закон сохранения энергии, представления о существовании различных видов энергии, количественные соотношения при переходах одних видов энергии в другие и т.д. В переводе с греческого энергия означает действие, деятельность. Глубокий смысл этого понятия раскрывается в полученном Эйнштейном соотношении эквивалентности энергии и массы: E = mc 2, где Е – энергия, m – масса вещества, с – скорость света в вакууме. В термодинамике энергия – это способность системы совершать работу.
Теплота и работа – характеристики способов передачи энергии: система может получить (отдать) энергию либо при нагревании, либо посредством совершения над нею работы. Совершение работы сопровождается сообщением системе частиц упорядоченности движения, а нагревание системы сопровождается нарастающей неупорядоченностью движения ее частиц.
Упорядоченность – взаимно коррелированное расположение частиц (элементов) системы. Упорядоченность проявляется в виде пространственной или временной корреляций.
Структура – определенное расположение, конфигурация частиц или элементов, составляющих систему. Наличие структуры равнозначно наличию упорядоченности.
Замкнутая система – система, не обменивающаяся энергией или веществом или тем и другим с окружающей средой. Иногда замкнутую систему называют изолированной.
Открытая система – система, связанная с окружающей средой и обменивающаяся с ней энергией, или веществом, или тем и другим.
Второе начало имеет несколько эквивалентных формулировок. Например, формулировка одного из основоположников этой дисциплины Кельвина: «Невозможен процесс, единственный результат которого состоял бы в поглощении теплоты от нагревателя и полного преобразования этой теплоты в работу». Формулировка другого основоположника Клаузиуса: «Невозможен процесс, единственный результат которого состоял бы в переходе энергии от более холодного к более горячему телу». Из обоих определений следует (и это самое главное), что в замкнутой системе при протекании любых преобразований энергии будет нарастать количество тепловой энергии, которую невозможно без дополнительных затрат энергии более высокого порядка перевести в другие формы энергии. А так как в замкнутую систему дополнительной энергии не поступает, то внутренние резервы рано или поздно истощаются, и тогда господствуют процессы распада существующих упорядоченностей, переход всех высших форм энергии в самую низшую – в тепловую энергию, иначе говоря, протекают процессы нарастания хаоса. Концом таких процессов и является достижение системой самого простого и неупорядоченного из всех возможных ее состояний – состояния ТДР.
Количественная направленность процессов преобразования энергии в системе выражается через понятие энтропии S. В замкнутой системе энтропия выражается соотношением, которое одновременно может служить ее определением:
где dE – сообщенная системе (или отнятая от нее) теплота, Т – температура системы. Таким образом, энтропия – это происходящее в протекающих процессах изменение тепловой энергии системы, отнесенное на один градус температуры. В ходе любых преобразований энтропия замкнутой системы растет. Следовательно, ее можно трактовать как меру неупорядоченности системы. Максимальная неупорядоченность – это состояние ТДР, ему соответствует максимальное значение энтропии: S = S max . Утверждение, что любые преобразования энергии в замкнутой системе ведут к росту энтропии, достигающей максимального для данной системы значения в состоянии ТДР, служит еще одной эквивалентной формулировкой второго начала.
Каждому термодинамическому состоянию можно приписать вероятность W, связанную с числом возможных способов, которыми это состояние достигается. Чем больше число таких способов, тем выше вероятность того, что данное состояние может реализоваться. Максимально возможной оказывается вероятность состояния, в котором все атомы (молекулы) распределены однородно, а энергия полностью рассеяна. Это и есть уже знакомое нам состояние ТДР. Больцман показал, что в замкнутой системе энтропия есть величина, пропорциональная логарифму вероятности данного состояния:
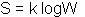
(2.24) Это соотношение имеет настолько глубокий смысл, что оно было выбито на надгробной плите могилы Больцмана. Понятно, что чем выше упорядоченность системы, тем меньше значение энтропии и тем маловероятнее достижение такого состояния. Этот вывод создал немалые трудности при попытках объяснить происхождение Вселенной и возникновение жизни: и то, и другое событие настолько маловероятно, что с этих позиций невозможно понять, как оно вообще могло реализоваться, если время существования Вселенной не является бесконечным. Но современные представления о Мире не распространяют выводы классической термодинамики на вещественную Вселенную, которая является открытой, а не замкнутой системой.
Итак, любая замкнутая система, какой бы исходной степенью упорядоченности она не обладала, с течением времени непременно перейдет в состояние ТДР. Но современное научное мировоззрение опирается на представления об открытости нашего мира, вокруг себя мы наблюдаем только открытые системы разных масштабов. Среди известных объектов не удается найти замкнутую систему в точном значении этого термина. Можно лишь говорить о той или иной степени приближения к равновесному состоянию тех или иных систем. А это значит, что в известном нам мире не существует как такового состояния ТДР, а есть лишь та или иная степень приближения к нему.
Плазма также существует только в состояниях, с той или иной степенью удаленности от ТДР, поскольку плазма образуется только в открытых системах. Тем не менее, в некоторых частных случаях можно с определенной степенью приближения рассматривать локальные области, заполненные плазмой, как находящиеся в квази-равновесном или ему подобном состоянии. Первой степенью приближения плазмы к равновесности считают установление в ней квазиравновесного распределения частиц одного сорта по скоростям (энергиям). Такое распределение было получено Максвеллом, оно названо максвелловским распределением по скоростям. На практике пользуются иным вариантом скалярной функции, называемой распределением частиц одного сорта по скоростям. Так, при фиксированном значении вектора 
функция распределения F определяет число частиц одного сорта в данном интервале скоростей 
, находящихся в определенном локальном местоположении. Для этого случая вводят скаляр f (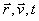 
):
(2.25)
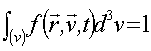
где n (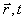
)– концентрация частиц данного сорта в конфигурационном пространстве [5]. Функция f определяет долю частиц, находящихся в данном единичном объеме, скорости которых лежат в интервале 
. Понятно, что интеграл этой функции по всем скоростям частиц в данном объеме равен единице, то есть охватывает все находящиеся там частицы.
Для данного единичного объема максвелловская функция f v определяется соотношением:
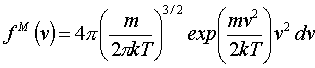
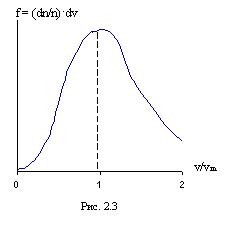
(2.26) Графически в приведенных координатах максвелловская функция распределения частиц по скоростям показана на рис.2.3.
(2.28) От функции распределения частиц по скоростям перейдем к функции их распределения по энергиям:
(2.29) Наиболее вероятная энергия в таком распределении характеризует степень нагретости тела, то есть температуру:
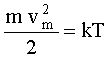
(2.30)
Для частиц сорта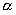 
величина Т определяет степень нагретости этих частиц, это температура частиц сорта 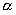, и ее можно обозначить символом 
. Среди частиц сорта 
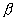также может установиться максвелловское распределение, но его наивероятнейшая энергия не обязательно совпадет с наивероятнейшей энергией частиц сорта 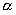. Таким образом, .
Следующей степенью приближения системы к равновесному состоянию считается случай, когда в многокомпонентной плазме среди частиц каждого сорта устанавливается свое максвелловское распределение, но у частиц каждого сорта оно отличается от распределения среди частиц других сортов. Для конкретности рассмотрим плазму, состоящую из частиц трех сортов: электронов, положительных ионов и атомов (молекул). Пусть у частиц каждого сорта установилось свое максвелловское распределение. Степень нагретости частиц каждого сорта характеризуется своей температурой, так что одновременно в плазме сосуществуют три разные температуры: электронная температура Т е , ионная температура Т i и атомная температура Та . Для плазмы, находящейся в умеренном внешнем электрическом поле, выполняется условие:
Состояние такой плазмы называют ионизационным равновесием. В этом случае обнаруживается прямая связь между электронной концентрацией (степенью ионизации) и электронной температурой, которая выражается соотношением, получившим название уравнения Саха:
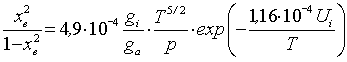
(2.31) где
;
р – давление в тор,
Т – в К,
U i – потенциал ионизации в эВ.
Из уравнения Саха следует, что электрические и оптические свойства плазмы, находящейся в состоянии ионизационного равновесия, зависят только от двух термодинамических параметров – от электронной температуры и давления.
Следующая ступень приближения плазмы к состоянию равновесия – максвелловские функции распределения по энергиям для всех частиц имеют одинаковые значения. Тогда можно написать, что: Te = Ti = Ta = T. Здесь Т – это единая температура всей системы. Степень ионизации такой плазмы определяется тем же уравнением Саха, но вместо электронной температуры Те в нем стоит общая температура Т. Вместо концентрации нейтральных частиц na вводится давление газа р, для чего используется известное газокинетическое уравнение:
(2.32) Самый правый вариант соотношения справедлив только при условии однократной ионизации плазмы. Эту степень приближения к равновесности называют тепловым равновесием.
В случае ионизационного и теплового равновесия распределение возбужденных атомов по энергетическим уровням при данной температуре Т описывается уравнением Больцмана (1.1):
(1.1) Здесь nk , no – соответственно населенности k-го уровня с энергией Ek , и основного уровня; gk – кратность вырождения k-го уровня (статвес); Go - статистическая сумма весов для частиц данного сорта:
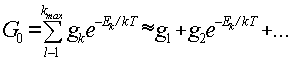
(2.33) Больцмановское квазиравновесное распределение возбужденных частиц по энергетическим уровням показывает, что с ростом энергии уровня его заселенность экспоненциально падает, так что появление инверсной населенности исключается, следовательно, не могут проявиться лазерные эффекты.
Самым сильным требованием к системе, позволяющим рассматривать ее как максимально приблизившуюся к ТДР, служит условие детального равновесия, когда частоты прямых и обратных процессов строго равны. Так, прямому процессу возбуждения атомов электронным ударом должен количественно соответствовать обратный процесс – девозбуждения атома электронным ударом и так далее. К сказанному остается добавить еще одно квазиравновесное состояние плазмы электрических разрядов в газах – локальное термодинамическое равновесие. О нем подробнее будет идти речь в дальнейшем, при рассмотрении систем оптической накачки лазеров. На этом мы завершим краткое знакомство с кинетикой плазменных процессов и рассмотрим особенности молекулы СО2 как основного элемента активной среды СО2 лазеров. Для дополнительного более подробного знакомства с физикой плазмы и, в частности, электрического разряда в газах, рекомендуются источники [3-6].
Молекула СО2 – трехатомная линейная молекула, три входящих в ее состав атома кислород – углерод – кислород выстроены в одну линию. Возбужденные состояния атома вызываются только одним видом движения – переходом электрона, получившего определенную порцию энергии извне, из основного состояния или из более низкого возбужденного состояния в более высокое возбужденное состояние. Таким образом, форма движения атома – это электронные переходы с одного дискретного энергетического уровня на другой. В отличие от этого у молекулы различают не один, а три вида движения:
- электронное движение – изменение положения электрона относительно атомных ядер;
- колебательное движение – периодические изменения относительного расположения ядер атомов, создающие колебательные их перемещения относительно друг друга.
- вращательное движение – периодические изменения ориентации молекулы как целого, иначе говоря, вращательные движения молекулы как единого целого.
Энергия молекулы Е есть сумма энергий каждого движения с включением тех добавок, которые связаны с энергиями взаимодействий различных видов движений:
(2.34) Энергия молекулы квантуется, и ее возможные состояния представляются в виде дискретных энергетических уровней. Так, изменение электронной энергии сопровождается также изменением колебательной и вращательной энергий, в результате возникают электронно-колебательно-вращательные спектры. Для простоты их называют просто электронными спектрами. Они обычно располагаются в видимой и УФ областях спектра.
Оценка количественных отношений трех видов энергии молекулы дает следующий результат:
(2.35)
где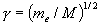 
, m e – масса электрона, М – величина порядка массы ядра молекулы, то есть 
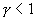. Обычное значение электронной энергии порядка единиц эВ, оно ближе к 10 эВ, энергия Екол порядка десятых – сотых долей эВ, а Евращ еще на порядок меньше. С точки зрения получения лазерных эффектов интересны спектры, возникающие при 
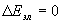, когда переходы совершаются только в пределах колебательно-вращательного спектра. Такой спектр ради краткости называют просто колебательным. Общее число колебательных степеней свободы у молекулы определяется условием: 3N – C, где N – число атомов в молекуле. С = 5 для двухатомной и линейной молекул и С = 6 для нелинейной многоатомной молекулы. Так, молекула СО2 имеет 4 колебательные и 2 вращательные степени свободы. Колебательные энергетические уровни молекулы вычисляются путем решения соответствующей задачи в рамках квантовой механики. Но используется и классическое приближение, в котором формы колебаний приобретают наглядный вид. Каждую из разновидностей колебаний называют модой, трехатомная молекула СО2 имеет 3 фундаментальные моды:
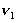- симметричная валентная мода;
- деформационная мода;
- асимметричная валентная мода.
В понятиях гармонических колебаний энергия каждого такого движения определяется соотношением:
(2.36) vk – колебательные квантовые числа, принимающие дискретные значения 0, 1, 2,... Самому низкому энергетическому уровню соответствует vk = 0, энергию этого уровня
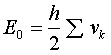
(2.37) называют нулевой энергией молекулы.
Энергетические уровни, для которых все квантовые числа vk за исключением одного равны нулю, а это одно значение равно единице, называют фундаментальными. Уровни энергии с одним квантовым числом большим единицы называют обертоном, а уровни энергии с несколькими отличными от нуля квантовыми числами называют комбинационными. На рис. 2.4 представлена упрощенная схема нижних колебательных уровней основного электронного состояния молекулы СО2 .
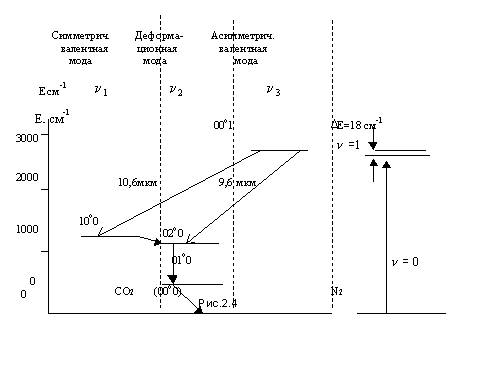
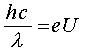
где с – скорость света в вакууме, 
– длина волны колебаний (в см). Учитывая, что h = 6,626.10– 34 [Дж.с], находим: 1 см–1 = 1,24.10– 4 эВ или 1 эВ = 8,07.103 см–1 = 1,6.10– 19 Дж. Уровни на рис.2.4 имеют трехцифирные обозначения, которые соответствуют трем квантовым числам, относящимся к соответствующим модам: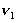
.
Например, 10о0 означает, что это фундаментальный уровень симметричной валентной моды (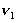
=1, ==0). Индекс квантового числа деформационной моды означает степень вырождения уровня этой моды. Так, запись 02о0 означает, что уровень является обертоном деформационной моды, состояние которого не является вырожденным (индекс 0).
На приведенной схеме справа присутствует изображение первого возбужденного колебательного состояния двухатомной молекулы азота. Добавка азота к двууглекислому газу играет существенную роль в процессе эффективного заселения верхнего лазерного уровня молекулы СО2 , но подробнее это обстоятельство мы обсудим несколько позже. Пока же добавим к уже сказанному, что излучение или поглощение электромагнитных волн на колебательных переходах молекулы описывается соотношением:
(2.38) Вращательная структура колебательных полос поглощения. У линейных многоатомных молекул энергия вращения определяется соотношением:
где j – вращательное квантовое число. Совокупность вращательных линий (на рис.2.4 они не могут быть выделены, поскольку сливаются с колебательными уровнями) образует соответственно S-, R-, Q-, P-, O- ветви. Распределение вращательных полос внутри ветви имеет максимум. У молекулы СО2 максимум для ветви Р имеет место при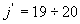 
. Существование вращательных линий позволяет в принципе осуществлять некоторые изменения частоты лазерного перехода (в небольших пределах, но и это иногда существенно). Что же делает молекулу двуокиси углерода пригодной для получения лазерного эффекта? В колебательном спектре этой молекулы (рис.2.4) имеется метастабильный уровень 00о1, время жизни возбужденных молекул на котором значительно превосходит время жизни на нижележащих уровнях 10о0 и 02о0.
В принципе этим обеспечивается возможность заселения метастабильного уровня, который при этом становится верхним лазерным уровнем, а два указанные нижележащие уровни при их быстрой очистке обеспечивают поддержание инверсной населенности между верхним и нижним состояниями молекул. Следовательно, лазерная генерация в среде молекул двуокиси углерода требует обеспечить эффективное возбуждение молекул СО2 , при котором заселяется преимущественно верхний уровень, а нижележащие уровни остаются практически свободными. Источником энергии накачки среды становится электрический разряд в газе, состоящем в основном из молекул СО2 . Но не каждый разряд и не в любом режиме может обеспечить выполнение необходимых требований. Перед Кумаром Пателем, создавшим первый молекулярный СО2 лазер, стояла непростая задача, которую ему удалось успешно решить.
Процесс возбуждения молекулы СО2 активно протекает в электрическом разряде, организуемом в среде таких молекул. В этом случае внутри каждой колебательной моды 
протекает интенсивный обмен энергией между молекулами и быстро достигается термализация – квазиравновесное состояние с распределением населенностей на разных уровнях моды по закону Больцмана. Это позволяет говорить о наличии внутримодовой температуры возбуждения 
:
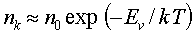
(1.1b) Следовательно, получить инверсную населенность между уровнями одной моды невозможно. Но между разными колебательными модами обмен энергией затруднен, поэтому температуры возбуждения у них различны. Это делает возможным при соответствующих условиях образовывать инверсную населенность между двумя уровнями, расположенными в разных модах.
Вернувшись к схеме нижних колебательных уровней (рис. 2.4), можно сделать заключение, что на роль верхнего лазерного уровня подходит расположенный в асимметричной моде метастабильный уровень
00о1, а в качестве нижнего уровня возможен либо уровень 02о0 из деформационной моды, либо уровень 1000 из симметричной валентной моды. Необходимые условия для получения инверсной населенности между указанными уровнями следующие:
- возбуждение уровней осуществляется в плазме электрического разряда в газе;
- неупругие электронные столкновения с молекулами СО2 должны избирательно возбуждать их до состояния 00о1, оставляя свободными уровни 02о0, 10о0 и все нижележащие уровни;
- уровни 02о0 и 10о0 должны достаточно быстро расселяться.
Возможно ли в принципе обеспечить выполнение этих условий? Ответ может быть положительным, если максимумы сечений возбуждения перечисленных уровней, зависящие от энергии электронов, разнесены между собой так, что появляется возможность подбором энергии электронов обеспечить преимущественное заселение верхнего уровня при относительно малой заселенности всех остальных. На рис.2.5 представлены экспериментально полученные зависимости сечений возбуждения трех уровней молекулы СО2 .
СО2 лазеры никогда не вошли бы в семейство мощных лазеров, если бы не удивительная особенность молекулы азота N2, которой воспользовался Пател. Первый колебательный уровень этой молекулы практически совпадает по энергии с верхним лазерным уровнем молекулы СО2 . Как видно из схемы уровней на рис. 2.4, разница энергий этих двух уровней составляет всего лишь 18 см–1, то есть ничтожно малую величину. Возбуждение же молекулы азота до первого колебательного уровня, как видно из рис.2.5, происходит при энергиях электронов от 2 до 2,5 эВ. При такой энергии электронов успешно протекает ионизация газовой среды. Если составить смесь двуокиси углерода с молекулярным азотом, то в самостоятельном разряде при энергии электронов порядка 2 эВ молекулы СО2 возбуждаются очень слабо, но идет активное возбуждение молекул азота до первого колебательного уровня. Далее, оказывается, что время жизни возбужденного первого колебательного уровня молекулы N2 очень велико (по масштабам времени микромира). Это связано с тем, что существует запрет на излучательное девозбуждение первого колебательного уровня молекулы азота, и энергия возбуждения будет сохраняться до тех пор, пока не произойдет неупругое соударение возбужденной молекулы с какой-либо частицей, способной забрать эту энергию. В смеси азота с СО2 практически все возбужденные молекулы азота резонансно передают свою энергию возбуждения молекулам СО2 , избирательно заселяя верхний лазерный уровень. Поэтому использование в СО2 лазерах не чистого двууглекислого газа, а его смеси с азотом, обеспечило возможность достижения почти идеального избирательного возбуждения верхнего лазерного уровня молекулы СО2 .
Для образования инверсной населенности наряду с обеспечением избирательного заселения верхнего уровня следует обеспечить поддержание нижележащих колебательных уровней в незаселенном состоянии. Главный источник заселения нижних уровней – термическое их возбуждение в нагретом разрядом газе. Избежать такого процесса можно лишь одним путем – сохраняя температуру газа ниже температуры термического возбуждения. Конкретно, температура газа в разряде не должна превышать (а еще лучше не приближаться к) 400 К.
Итак, теперь можно сформулировать требования к разряду, в котором смесь азота и СО2 способна будет обеспечить возникновение инверсной населенности у молекул СО2 , что приведет к появлению лазерного эффекта: при температуре тяжелых частиц, не превышающей 400К, электронная температура должна составлять 2 - 2,5 эВ. Это разряд, создающий сильно неравновесную плазму с очень большим отрывом электронной температуры от температуры газа. В таком разряде необходимо обеспечить очень эффективный отвод тепла из зоны, где оно выделяется, то есть из области протекания тока. Частично помогает решать эту проблему добавление к рабочей смеси еще и гелия в значительных количествах. Теплопроводность гелия в 6 раз выше теплопроводности основных газов, а высокий потенциал ионизации (24,5 В) препятствует ионизации, что исключает его заметное влияние на электрические характеристики разряда.
Теперь мы можем перейти к центральному вопросу – существует ли разряд, в котором выполняются сформулированные выше требования: при практически холодном газе электронная температура должна быть порядка двух электрон-вольт. Такой разряд существует, он называется тлеющим разрядом, и если бы его не было, то не существовал бы и СО2 лазер.
Тлеющий разряд. В технических устройствах и в научных исследованиях используются разряды различных типов, отличающиеся давлением газа, силой разрядного тока, условиями отвода тепла и другими характеристиками. Для создания в разряде инверсной населенности (для лазерной накачки) необходим разряд особого типа. В случае смеси двух газов – СО2 и N 2 – пригодным для этих целей стал тлеющий разряд, самоподдерживающийся разряд с холодным катодом. Характерный признак тлеющего разряда – наличие в нем области катодного падения напряжения, в которой образуется большой по величине объемный положительный заряд.
Протяженность этой области порядка нескольких сантиметров, и на этом участке падение напряжения достигает значений от примерно 100 до 400 В и больше. Если расстояние между катодом и анодом меньше того, которое необходимо для образования катодной области, то разряд не возникает. При расстояниях между электродами от 10 см и выше за областью катодного падения образуется положительный столб, отделяемый от анода относительно узкой областью анодного падения напряжения. Для накачки СО2 лазеров используется положительный столб тлеющего разряда. Он представляет собой слабо ионизованную плазму, поддерживаемую внешним электрическим полем. Тлеющий разряд может существовать при давлениях газа от 10- 2 до 10 тор и разрядных токах, не превышающих ~10-1 А. При очень низких токах или давлениях вместо него образуется так называемый темный таунсендовский разряд. Превышение током или давлением указанных верхних пределов, как видно из графика на рис. 2.6, переводит тлеющий разряд в дуговой разряд, протекающий уже не при холодном, а при горячем катоде. Дуговой разряд неприемлем для накачки СО2 лазеров.
Тлеющий разряд изучается уже более 100 лет, его подробности описаны во всех учебниках и монографиях, посвященных электрическим разрядам в газах. Кроме областей катодного и анодного падений напряжения и положительного столба в разряде этого типа выделяют и другие структурные детали, которые для наших целей не представляют интереса. Для ознакомления с тлеющим разрядом во всех деталях можно рекомендовать, например [3].
Тлеющий разряд создается в разрядной трубке, представляющей собой обычно цилиндрическую стеклянную трубку радиуса R, в торцах которой по ее оси устанавливаются противостоящие электроды – анод и катод. Нижний предел радиуса трубки определяется условием: le << R, где le - длина свободного пробега электрона. Под действием внешнего электрического поля напряженностью Е, поддерживающего горение разряда, в плазму положительного столба передается энергия. Непосредственными приемниками энергии поля являются заряженные частицы, прежде всего электроны, как наиболее легкие из этих частиц. Поскольку классический тлеющий разряд может существовать лишь при низких давлениях газа (не более 10 тор) и при слабых токах, то вероятность столкновения электронов с молекулами газа в столбе разряда невелика, и объемными процессами ионизации и рекомбинации в первом приближении можно пренебречь. Источником электронов служит область катодного падения напряжения, выполняющая по отношению к столбу роль своеобразного катода. Однако пусть не очень частые неупругие столкновения электронов с молекулами азота не сопровождаются ионизацией, но они возбуждают эти молекулы, а энергия их возбуждения передается при межмолекулярных столкновениях молекулам углекислого газа, обеспечивая направленное заселение верхнего лазерного уровня.
В области столба разряд заполняет все сечение трубки, если её радиус ограничивается условием: le << R, где le – длина свободного пробега электрона. Обычно речь идет о радиусе порядка 1,5 см. Сразу после включения разряда протекает процесс диффузии электронов на стенки трубки, в результате на них возникает отрицательный заряд, создающий поперечное электрическое поле. Это поле тормозит, а затем и полностью прекращает диффузию одиночных электронов на стенки. Но возникает новый тип диффузии, получивший название амбиполярной диффузии. Электроны объединяются, но не рекомбинируют, с ионами и в таком парном нейтральном единстве движутся к стенкам, где рекомбинируют и отдают стенкам тепло. Это тепло через стенки должно выноситься в окружающую среду.
Особенности классического тлеющего разряда таковы, что не могут обеспечить получения больших мощностей в лазерном луче. В дальнейшем будет показано, что проблему увеличения мощности СО2 лазера удалось решить благодаря открытию разновидности тлеющего разряда, при которой основные его особенности – диффузная форма разряда, отрыв электронной температуры от температуры молекул газовой среды, удалось сохранить при высоких давлениях и больших токах. При такой форме разряда объемные процессы ионизации и рекомбинации протекают в объеме положительного столба, а вынос тепла осуществляется потоком газа через зону разряда, не вовлекая в эти процессы стенки разрядной камеры. В этой связи имеет смысл рассмотреть основные особенности газоразрядных процессов, возникающие не только при классической форме тлеющего разряда.
Прикладываемое к электродам разрядного промежутка напряжение вызывает протекание электронного тока от катода к аноду и ионного тока в обратном направлении. Направленное движение зарядов накладывается на хаотическое (тепловое) движение всех газовых частиц. Основную энергию от продольного электрического поля получают электроны, но дальнейшее их движение сопряжено с взаимодействиями с тяжелыми частицами газовой среды, протекающими как упруго, так и неупруго, что сопровождается изменениями движения и обменом энергией с этими частицами. В таких условиях направленная составляющая движения зарядов (ток) проявляется как относительно слабый дрейф зарядов и этот эффект называют переносом зарядов, а характеризующий направленность коэффициент называют коэффициентом переноса. Оценка отношения скорости переноса к скорости теплового движения v:
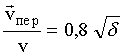
(2.39) 
Таким образом, скорость переноса на 2 порядка меньше скорости теплового движения частиц. В случае переноса электрических зарядов плотность тока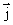 
и скорость переноса 
пропорциональны напряженности электрического поля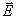 
:
(2.40)
Коэффициент пропорциональности 
называют подвижностью, а коэффициент пропорциональности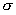 
– удельной электропроводностью. Оба коэффициента связываются с микрохарактеристиками среды. Так, уравнение движения электронов
(2.41)
где заряд электрона е = 4,8.10–10 СГСЭ = 1,6.10–19 Кл в СИ, масса электрона me= 9,1.10–28 г,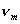 
– частота столкновения электрона с другими частицами.
В случае стационарности (установившееся горение разряда) dveпер /dt = 0 и
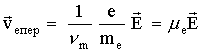
(2.40a) откуда находится подвижность электронов:
(2.42)
Если размерность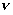 
- в [c- 1], то размерность
будет [см2 /(В.с)]. Соответственно для подвижности ионов получено соотношение:
(2.42a)
>>
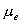. В таблице 2.4 даны экспериментальные значения подвижности ионов в собственном газе, которые можно сравнить со значениями 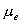из предыдущей таблицы. Поскольку плотность электрического тока в разряде равна:
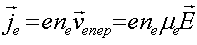
(2.43) то удельная электропроводность:
(2.44)
Если nе– в см-3, а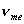 
– в с-1, то
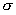– в Ом-1.см-1. В литературе можно встретить вместо Ом-1 другое название единицы электропроводности – Сименс: См = Ом-1.
Таким образом, для определения удельной электропроводности плазмы, этой характеристики переноса электрических зарядов, необходимо знать частоту столкновений соответствующих частиц при их движении во внешнем электрическом поле. Эту частоту следует усреднить по всему ансамблю данных частиц, воспользовавшись функцией их распределения по скоростям. На подробностях такой процедуры здесь нет смысла останавливаться, она рассматривается в курсах физики плазмы, например в [4,5].
Общие представления о процессах, происходящих при электрических разрядах в газах, конкретизируются при рассмотрении положительного столба тлеющего разряда следующим образом. Характеристики столба вдоль оси меняются слабо, что позволяет считать градиент потенциала в этом направлении постоянным, не зависящим от общей длины столба: dU/dx = const. Отсюда следует, во-первых, что средняя энергия электронов также постоянна вдоль оси, то есть электронная температура постоянна Te (x) = const. Во-вторых, так как d2 U/dx2= 0, то в каждой точке вдоль оси соблюдается условие квазинейтральности: ne = ni. В радиальном направлении не сохраняется однородность пространственного распределения параметров. Для оценочных прикидок параметров положительного столба тлеющего разряда можно воспользоваться приведенными соотношениями и экспериментальными данными, содержащимися в таблицах 2.3, 2.4.
Обычно классический тлеющий разряд создается в разрядной трубке, представляющей собой цилиндрическую стеклянную трубку радиуса R, в торцах которой по ее оси устанавливаются противостоящие электроды – анод и катод. Как отмечалось выше, рекомбинация наиболее активно происходит на стенках разрядной трубки, куда электроны и ионы попарно попадают в результате амбиполярной диффузии, поскольку объемная рекомбинация оказывается маловероятной. Что же собой представляет диффузия и, в частности, амбиполярная диффузия?
Диффузией в газе называют процесс перемещения заряженных или нейтральных частиц из области с большей их концентрацией в область с меньшей концентрацией. Скорость диффузии частиц в собственном газе определяется соотношением:
(2.45) где n - концентрация частиц, а D – коэффициент диффузии. Если vд выражена в см/с, n – в см-3, то размерность D – см2 /с. При протекании диффузии только в направлении оси Х ее скорость определяется соотношением:
(2.46) Из кинетической теории газов следует, что коэффициент диффузии ионов в собственном газе равен:
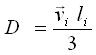
(2.47) - средняя тепловая скорость ионов, li – длина их свободного пробега. Например, экспериментально определенное значение коэффициента диффузии ионов в азоте при давлении 1 тор равно ~ 23 см2/с, а в СО2 – 18 см2/с.
Для электронов коэффициент диффузии выражается в такой же, как и для ионов, форме
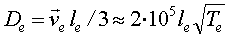
(2.48) Обычные значения De для интересующих нас газов порядка 105 см2/с, то есть De >> Di. Так как li ~ T/ p, то при Т = const имеем Di, p = const, а при p = const Di ~ T3/2. Среднее перемещение иона за время t: x = .
Из теории также вытекает, что коэффициент диффузии связан с подвижностью заряженной частицы соотношением Эйнштейна:
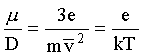
(2.49) Для ионов, температура которых примерно равна температуре нейтральных частиц, правая часть (2.49) приводится к виду:
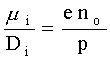
(2.50) а для электронов, когда Те >Тi, введение давления p невозможно, и для них соотношение сохраняется в виде (2.49) с заменой Т на Те.
В столбе тлеющего разряда под действием продольного электрического поля между электродами осуществляется диффузионный процесс переноса зарядов, создающий электрический ток разряда. При этом протекают процессы неупругих столкновений электронов с молекулами, сопровождающиеся возбуждением молекул газа. Одновременно происходит диффузия заряженных частиц и в радиальном направлении, от оси разряда к стенкам. Радиальное поле тормозит движение электронов к стенкам и ускоряет движение ионов в этом направлении. При определенной концентрации избыточных электронов на стенке поле достигает такой величины, что скорости диффузии электронов и ионов уравниваются, частицы с разноименными зарядами начинают двигаться к стенке попарно и там рекомбинировать. Такой тип диффузии впервые изучил и теоретически описал Шоттки в 1924 году. Он же назвал такую диффузию амбиполярной.
Пусть выполняется условие: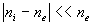 
. Электроны и ионы движутся с одинаковой скоростью к стенке и эта скорость равна:
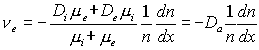
(2.51)
Da - коэффициент амбиполярной диффузии. С учетом того, что
>>
и De >> Di имеем следующее выражение для определения Da:
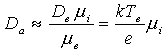
(2.52) (правая часть соотношения получена с учетом формулы Эйнштейна). Напряженность радиального поля ЕR автоматически устанавливается на значении:
(2.53) где R – характерный масштаб градиента плотности зарядов, в данном случае – это радиус разрядной трубки.
Основные следствия теории положительного столба тлеющего разряда. Теория положительного столба классического тлеющего разряда была разработана в своей основе в 20-е – 30-е годы предыдущего века. В положительном столбе заряженные частицы попадают под воздействие как аксиального, так и радиального электрических полей. Здесь коснемся лишь некоторых следствий теории, представляющих интерес для темы данной книги.
а) Радиальное распределение зарядов. Под действием радиального поля протекает амбиполярная диффузия заряженных частиц. Уход заряженных частиц из осевой зоны компенсируется их поступлением из зоны катодного объемного заряда и отчасти в процессах объемной ионизации, протекающей при неупругих соударениях электронов с молекулами. Частоту таких соударений обозначим через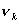 
.
Уравнение баланса заряженных частиц записывается в форме:
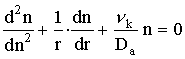
(2.54) Его решением служит бесселева функция нулевого порядка Jo c действительным аргументом
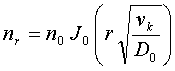
(2.55) где nо - концентрация заряженных частиц на оси разряда. У стенки (r=R) заряд очень мал, поэтому , откуда из таблиц бесселевых функций получаем . Подставив в (2.55) это значение, находим:
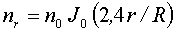
(2.55a) Таким образом, распределение зарядов по радиусу трубки близко к параболическому.
б) Связь электронной температуры с напряженностью аксиального электрического поля Ех [3]. Энергия электрона в столбе разряда определяется балансом, состоящим из получаемой им энергии от внешнего электрического поля и потерями энергии при столкновениях. Приобретаемая энергия: еЕ х vпер. Теряемая энергия:
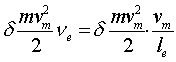
Здесь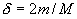 
– доля теряемой электроном энергии при упругих соударениях. При неупругих соударениях эта доля 
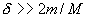. Так как mv2/2 = kT, то потери можно записать в виде 
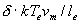. Уравнение баланса энергии для электрона выглядит так:
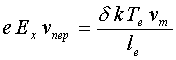
(2.56) Но vпер /vm ~ и, в конечном счете
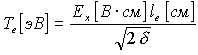
(2.57) в) Электронная температура. Введем обозначение:
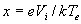, где Vi – потенциал ионизации. Формула для определения Те как функции радиуса трубки R, давления газа р с учетом рода газа находится из соотношения для скорости ионизации в расчете на один электрон:
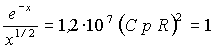
(2.58) Здесь 
,
a – эффективность ионизации, р – в тор, Vi – в вольтах, – в см2
/(В.с), Те – в К.
Для интересующих нас газов коэффициент эффективности ионизации «а» приведен в таблице 2.5.
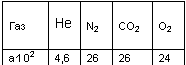
В 1964 году Пател запустил первый СО2 лазер. Достигнутый им успех определился двумя факторами: он использовал смесь СО2 и N 2 и применил для накачки такой смеси тлеющий разряд. Первые лазеры имели оформление, представленное на рис. 2.8.
СО2 лазеры такой конструкции называют диффузионными, так как тепло от разряда отводится процессом диффузии заряженных и нейтральных частиц к стенкам трубки. Для интенсификации радиального теплопереноса используют водяное охлаждение стенок, окружая их стеклянной водяной рубашкой (3). Торцы трубки герметично закрывают прозрачными для ИК-излучения выходными окнами (2). Поскольку СО2 лазер генерирует излучение в диапазоне длин волн от 9 до 11 мкм (главным образом на волне 10,6 мкм), то стекло и кварц, как и некоторые другие оптические элементы, работающие в видимом и в ближнем ИК диапазонах излучения, для создания окон, прозрачных в этом дипазоне длин волн, непригодны, нужны особые материалы и о них речь впереди.
Характерные размеры первых СО2 лазеров: диаметр разрядной трубки от 1 до 10 см, длина трубки до 2 м. При создании газоразрядного лазера необходимо решить три основные проблемы:
- проблема организации разряда в трубке (камере);
- проблема отвода тепла, выделяющегося в зоне разряда;
- проблема «порчи» газовой смеси, главным образом из-за диссоциации молекул в разряде: СО2 
СО + О. Рассмотрим каждую из этих проблем.
Организация разряда складывается из следующих элементов:
- выбор компонентов газовой смеси и соотношений их парциальных давлений;
- выбор общего давления газа;
- выбор источника электропитания и его параметров;
- установление зависимостей параметров среды (Та
, Те
, коэффициент усиления среды на длине волны лазерного излучения, выходная мощность излучения) от геометрических размеров трубки (камеры), от состава газа, давления, интенсивности охлаждения, от плотности разрядного тока и напряженности электрического поля.
В лазерах диффузионного типа использовался типичный состав газовой смеси: СО2 , N 2 , He. Нахождение оптимального соотношения парциальных давлений компонентов предпочтительно определяется экспериментально.
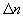от парциального давления азота N 2 при разрядном токе 30 мА, парциальном давлении двуокиси углерода в трубке диаметром 34 мм. В данном случае оптимум достигается при парциальном давлении азота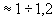 
Тор, то есть при значениях
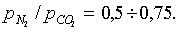
В других случаях это соотношение может быть иным, но не должно превышать ~ 3. Выбор парциального давления гелия более свободен, и соотношение парциального давления Не к парциальному давлению СО2 колеблется от 1 до 10.
Общее давление газа, как было отмечено при рассмотрении тлеющего разряда, не должно превышать 10 Тор. Учитывая, что доля молекул СО2 в смеси газов не превышает 50%, а обычно из-за добавки гелия она существенно ниже, делаем вывод, что концентрация излучающих центров в активной лазерной среде довольно низкая.
Проблема отвода тепла из зоны разряда – одна из самых существенных при попытках повысить выходную мощность лазера. При напряженности электрического поля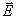
и плотности разрядного тока
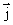в каждом единичном объеме газа выделяется джоулево тепло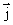
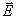. Температура газа, нагреваемого этим теплом, определяется из соотношения:
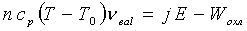
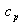– теплоемкость при р = const,
Т о
– комнатная температура, 
– частота соударений электрона с атомом (слабо ионизованная плазма) или с ионом (сильно ионизованная плазма),
– Wохл – энергия, уносимая из зоны разряда в процессе охлаждения.
При радиальном охлаждении в режиме диффузии эта энергия не велика, что накладывает жесткие ограничения на предельно допустимые значения R, p, j, а также на предельную мощность излучения, которую можно достигнуть в лазере данного типа. Электронная температура в тлеющем разряде, как уже говорилось, достигает порядка 2 эВ. Что же касается предельно допустимой температуры нагрева газа, то представление о ней можно получить из графика, приводимого на рис. 2.10.
График отображает зависимости скорости обмена колебательной энергией КТ между молекулами N2 и СО2 , скорости релаксации верхнего лазерного уровня 
молекулы СО2 , и скорости релаксации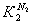 
верхнего колебательного уровня молекулы N2. В сочетании с возрастающей интенсивностью термического заселения нижних лазерных уровней молекулы СО 2 это ведет к резкому снижению инверсной населенности или к полному ее исчезновению.
Выбор параметров источника питания. Блок – схема источника питания непрерывного СО2 лазера представлена на рис.2.11.
Потребляя напряжение от сети электропитания 220/380 вольт переменного напряжения, он состоит из регулятора напряжения (1), высоковольтного трансформатора (2) и высоковольтного выпрямителя (3). Отдельным блоком в источник питания входит прибор инициирования разряда (4). Инициирование разряда представляет собой особую задачу, для реализации которой используют, кроме отдельного блока питания, поджигающий электрод, входящий в состав разрядной трубки. Система поджига создает импульс высокого напряжения, способный обеспечить пробой холодного газа в разрядном промежутке, либо создается высокочастотный импульс, способный обеспечить предварительную ионизацию газа в этом промежутке.
Параметры основного источника питания определяются электрическими свойствами разрядного промежутка в процессе горения в нем разряда и необходимыми пределами их изменения. Формирование требований к источнику питания опирается, как минимум, на знание вольтамперной характеристики (ВАХ) разряда. ВАХ зависит от геометрии разрядной трубки (камеры), от состава и давления газов, от степени ионизации плазмы (от электропроводности). Учет всех факторов, влияющих на ВАХ, в принципе может быть осуществлен расчетным путем, но это сложный и не всегда надежный путь. Поэтому чаще предпочитают находить ВАХ экспериментально для каждого конкретного устройства. Качественное представление о характерных особенностях ВАХ диффузного СО2 лазера можно получить на конкретном примере, представленном на рис. 2.12.
Эти зависимости получены при следующих параметрах лазера: диаметр разрядной трубки 20 мм, общее давление газовой смеси р = 2,5 Тор. Кривая (1) получена в условиях, когда использована смесь только двух газов – СО2 и N2 при отношении парциальных давлений 
;
кривая (2) – это ВАХ при наполнении трубки тремя газами с отношением парциальных давлений: 
Общее давление газа и разрядный ток те же, что и при получении кривой (1). Обе зависимости падающие, то есть с повышением разрядного тока напряжение на разрядном промежутке уменьшается. Для нормального поддержания разряда при таком характере ВАХ необходимо ставить во внешнюю электрическую цепь балластное сопротивление.
С ростом разрядного тока растет концентрация электронов и увеличивается электропроводность газа. Качественно представление о характере такого роста дает экспериментальный график на рис. 2.13. Зависимость ne от ip получена в тех же условиях, что и ВАХ на рис. 2.12. Но следует иметь в виду, что возможности повышения тока в тлеющем разряде ограничены пределами, о которых говорилось ранее.
Рассмотрим идеальный случай, когда мощность СО2 лазера определяется соотношением:
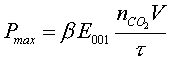
(2.59)
Здесь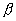 
– квантовый к.п.д. молекулы СО2 , 
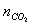– концентрация этих молекул в разряде, Е001 – энергия верхнего лазерного уровня, V – объем активной среды, 
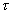- время опустошения нижнего лазерного уровня. Для конкретной лазерной системы соотношение (2.59) определяет ее предельную выходную мощность, превзойти которую принципиально невозможно. Действительно, квантовый к.п.д.
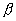= Еизл/ Е001 определяет предельно возможное отношение излучательной энергии Еизл к энергии верхнего лазерного уровня, иначе, к энергии накачки, и для данной молекулы это есть постоянная величина. Для молекулы СО2
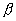= 0,41. Величина Е001 для молекулы СО2 равна 0,3 эВ. В соотношении (2.59) полагают, что вся энергия накачки расходуется только на возбуждение верхнего лазерного уровня. Варьировать можно лишь тремя параметрами: концентрацией молекул СО2 , объемом разрядной области V и величиной
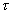, которая напрямую зависит от интенсивности отвода тепла, иначе говоря, от интенсивности охлаждения газа. В непрерывном лазере
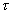заменяют на время 
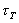отвода тепла, выделяемого в зоне разряда, во внешнюю среду.
Рассмотрим работу лазера в диффузионном режиме. Экспериментальные данные показывают, что минимальное время отвода тепла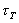
= R/u, где R – радиус трубки, u – скорость дрейфа частиц к стенкам, равно ~ 5.10–2 с. Подставив это значение вместе с константами
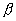и Е001 в (2.59), получим:
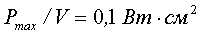
(2.60)
Далее, V = 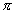R2L, где L – длина разрядного промежутка. Как показывает опыт, увеличивать радиус трубки свыше определенного предела невозможно, поскольку это ведет к увеличению времени
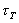и резкому ухудшению вывода тепла, то есть к наступлению перегрева газа в разрядном промежутке. Практика показывает, что предельный радиус разрядной трубки не может превышать 1,5 см. С учетом сказанного, увеличивать объем разрядной области в трубке можно только за счет увеличения длины, но не поперечного сечения. Тогда предельная мощность диффузионного лазера на единицу длины примерно равна
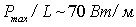
Но у реальных лазеров в лучшем случае достигают примерно половину этой величины. Таким образом, единственный путь повышения мощности диффузного лазера – увеличивать его длину. Например, для получения мощности излучения порядка 1 кВт длину разрядной части лазера необходимо сделать не менее 30 метров. В начальный период создания СО2 лазеров было предложено «складывать» длинные трубки в виде колен, как схематично показано на рис. 2.14.
Связь между коленами осуществляется поворотными зеркалами или призмами. Такой вариант сложения длинных трубок применяется и в наши дни в некоторых конструкциях непрерывных СО2 лазеров малой и средней мощности, выпускаемых промышленностью. Например, лазер мощностью 100 Вт под названием «Киль» имеет 8 колен, каждое из которых представляет собой трубку длиной примерно 40 см. Отдельная трубка снабжена электродами и питается от своего источника электроэнергии, то есть источник питания разбивается на отдельные секции по числу «колен».
Повышение мощности за счет интенсификации охлаждения быстрой прокачкой газа.
Поскольку диффузный режим исчерпал свои возможности повышения удельной мощности лазера, исходный выход из тупика был найден на путях интенсификации охлаждения газа. Пришлось отказаться от метода естественного радиального отвода тепла, не требовавшего дополнительных технических устройств, и перейти к системам прокачки газа через разрядный объем вдоль оси трубки. Подобный метод получил название продольной прокачки газа. Один из вариантов подобной системы приведен на рис. 2.15.
Проток газа через трубку в продольном (осевом) направлении позволяет снизить входящее в соотношение (2.60) время отвода тепла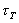
по сравнению с диффузионным режимом более чем на порядок, так что 
c. Соответственно возрастает удельная мощность излучения, снимаемая с единицы длины трубки, она достигает нескольких сотен ватт на метр длины. Скорости потока газа вдоль оси трубки достигают 50 м/с и более.
При конструировании систем прокачки газа необходимо знать предельный энерговклад на единицу массы газа qmax, при котором тепловой режим в разряде не превысит критического уровня, то есть ~ 400 К. Эта величина определяется условием:
где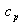
– теплоемкость газа при постоянном давлении, 
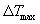– максимально допустимый прирост температуры газа, не приводящий к превышению критического уровня, 
– к.п.д. лазера по вводимой мощности, равной:
Pизл – излучаемая мощность. Энерговклад на единицу массы газа определяется соотношением
где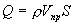 
– массовый расход протекающего газа, 
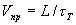– скорость прокачки. Необходимо выполнение следующего условия:
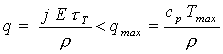
Оценки показывают, что при продольной прокачке q max 
700 Дж.
Поперечная прокачка. Дальнейшая интенсификация охлаждения активной среды и подъем на этой основе мощностного предела СО2 лазеров стали возможными в результате внедрения двух принципиально новых физико-технических решений. Первое состояло в реализации идеи замены продольной прокачки газа через разрядную область на поперечную прокачку. Второе решение – одновременное введение поперечного электрического разряда. Совместное использование этих двух решений совершило революционные изменения в развитии СО2 лазеров, и не только их. Так, вместо выглядевших архаично стеклянных разрядных трубок стали применяться разрядные камеры с большим поперечным сечением разрядной зоны, изготавливаемые из пластмасс, стеклопластиков или металлов с внутренней футеровкой стенок. За счет увеличения поперечного сечения разрядной зоны объемы активной среды удалось увеличить, не меняя при этом существенно длины лазера. Но, конечно, пришлось пожертвовать простотой технических решений. Пример устройства лазера с поперечными электрическим разрядом и прокачкой газа схематично показан на рис. 2.16.
К разрядной камере (1) пристыковывается газодинамический тракт (3), в состав которого входит теплообменник (4), вентилятор (5) и аэродинамическая решетка (6), выравнивающая поток газа перед его вхождением в зону разряда. Поперечный поток газа и поперечный электрический разряд располагаются во взаимно перпендикулярных плоскостях. Поперечная прокачка обеспечивает существенное сокращение времени выноса тепла из зоны разряда и позволяет несколько поднять скорость прокачки газа, но не слишком сильно, так как возникает опасность «выдувания» разряда потоком газа. Тем не менее, оба фактора позволяют увеличить предельную мощность в несколько раз по сравнению с системами продольной прокачки газа.
Устройство разрядного промежутка лазера, схематично изображенного на рис. 2.16, рассмотрим на конкретном примере. Для этого воспользуемся описанием непрерывного лазера, созданного в Новосибирском институте прикладной механики АН [7]. Вынесенная из камеры электродная система схематично изображена на рис. 2.17. Электроды выполнены из медных полированных трубок диаметром 10 мм и длиной 100 см. Трубки изнутри охлаждаются водой. Расстояние между анодом и катодом варьируется в пределах от 4 до 8 миллиметров. Падение напряжения на разрядном промежутке составляло 1 кВ. Обозначенный стрелками поток газов ограничивается выполненными из стекла дефлекторами. Рабочее давление в камере в этом конкретном случае доводилось до 50 Тор, но наиболее приемлемый интервал составлял от 10 до 20 Тор. Скорость потока газов – до 50 м/с
Особого внимания заслуживает факт использования в этой установке вспомогательного электрода (3), питавшегося от высокочастотного источника тока и создававшего в разрядном промежутке, наряду с основным разрядом, дополнительный ВЧ разряд между этим электродом и анодом (2). Вспомогательный электрод располагался параллельно основным электродам на удалении 2 см от катода (1). По мнению авторов разработки, ВЧ разряд (его частота равнялась 1,5 МГц) очищал поверхности медных электродов от возникавших на них окисных пленок, чем обеспечивалось стабильное горение основного разряда. Одновременно создавалась возможность подъема давления газа в камере, которое от 2 до 5 раз превышало предельное давление в классическом тлеющем разряде. На самом деле, как станет ясно из дальнейшего обсуждения проблемы повышения удельной мощности СО2 лазера, ВЧ разряд содействовал возникновению нового типа тлеющего разряда, отличного от классического. Максимальная выходная мощность приводимого в качестве примера непрерывного лазера достигала 800 Вт.
Системам с поперечной прокачкой газа наряду с наглядными достоинствами присущи и определенные недостатки. Прежде всего, необходимо учитывать смещение зоны разряда в потоке газа от центрального положения, так называемый эффект «выдувания». Например, при скорости потока 50 м/с смещение разряда по потоку составляет 3 см. Поскольку величина смещения зависит от скорости потока, то изменение этой скорости в процессе работы лазера приводит к его разъюстировке (зеркала остаются неподвижными). Далее, при создании такого лазера необходимо обеспечивать достаточно высокие требования к газодинамике прокачного тракта, поскольку неравномерности газового потока по сечению и во времени нежелательны. Наконец, в режиме непрерывной генерации стабильность разряда обеспечивается в довольно узком интервале давлений газа, силы разрядного тока, соотношения компонентов газовой смеси. Поэтому применяются различные способы повышения стабильной работы таких лазеров. Один из примеров – использование вспомогательного ВЧ – разряда. Известны и другие способы, применение которых не всегда дает желаемые результаты. Например, для стабилизации пробовали использовать магнитное поле, ориентированное так, чтобы движение электронов и ионов под его воздействием было направлено навстречу потоку газа. Тогда подбором напряженности магнитного поля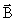 
в принципе можно скомпенсировать снос заряженных частиц. Если скорость сноса u, то баланс процесса определяется соотношением:
(2.61)
Например, в разряде с составом рабочей смеси СО2 : N2: He = 1 : 1,2 : 4 при общем давлении р
19 Тор и Е/р
18 В/(см.Тор) из соотношения (2.61) получают: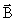
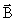/u = 10 Гс.с/м.
Применение поперечной прокачки газа позволило до конца использовать возможность повышения предельной мощности СО2 лазеров за счет интенсификации охлаждения разрядного промежутка. Дальнейшее движение в этом направлении предполагает, согласно (2.60), повышение концентрации молекул СО2 , то есть повышение общего давления газа. Но, как следует из графика рис.2.6, при превышении верхнего предела давления в 10 Тор классический тлеющий разряд переходит в дуговой разряд. Казалось бы, этот путь неприемлем. Но выход из положения удалось найти. Для этого нужно было понять, почему увеличение давления газа вызывает переход тлеющего разряда в дуговой.
В разряде одновременно идут два процесса – ионизация нейтрального газа и возбуждение атомов (молекул) за счет их соударений с электронами. Процесс ионизации требует более высоких затрат энергии, чем процесс возбуждения. А в том случае, когда мы стремимся к получению преимущественного возбуждения верхнего лазерного уровня молекулы СО2 , что достигается через возбуждение молекулы азота при энергии электронов около 2 эВ, то необходимо при этом обеспечить незаселенность нижних уровней, то есть сохранять температуру газа ниже 400 К. При увеличении давления резко возрастает число актов рекомбинации и, соответственно, необходимо увеличить число актов ионизации, без чего разряд не сможет существовать. Приходится увеличивать напряженность электрического поля и разрядный ток. Тогда резко возрастает нагрев электродов и вместо автоэлектронной эмиссии возникает термоэмиссия, сопровождающаяся переходом тлеющего разряда в дуговой. Конечно, одновременно увеличивается и джоулево тепло, выделяющееся в разряде, но с этим мы знаем, как бороться. Возникает дилемма: чтобы возбуждать при высоком давлении верхний лазерный уровень, оставляя незаселенными нижние уровни, необходимы более низкие значения напряженности электрического поля, чем этого требуют процессы ионизации, при которых разряд сможет существовать. Но при соответствующих этим требованиям значениях напряженности поля тлеющий разряд перейдет в дуговой. Это противоречие можно разрешить, если разделить в разряде процессы ионизации и возбуждения верхнего лазерного уровня. Для реализации такой идеи необходимо было найти независимый источник ионизации газа в разрядном промежутке, после чего осуществить в нем протекание основного разряда уже при сравнительно низких значениях напряженности внешнего поля.
Ионизация разрядного промежутка с применением внешнего источника ионизации. Внешний источник ионизации может представлять собой:
- вспомогательный разряд, параметры которого обеспечивают протекание в разрядном промежутке ионизационных процессов достаточной интенсивности;
- источник высокоэнергетичных ультрафиолетовых, рентгеновских или гамма-излучений, способных ионизовать активную лазерную среду;
- источник вводимых в разрядный промежуток быстрых электронов, производящих первичную ионизацию;
- источник других быстрых корпускулярных частиц, таких как протоны или нейтроны.
Современная техника мощных лазеров использует из этого перечня два типа источников ионизации: вспомогательный разряд и поток быстрых электронов.
Непрерывный СО2 лазер с вспомогательным разрядом. Один из вариантов такой системы был рассмотрен выше – это СО2 лазер с вспомогательным ВЧ разрядом. Роль ВЧ разряда состояла в осуществлении дополнительной ионизации активной среды, что позволило несколько снизить необходимую напряженность электрического поля основного разряда и за этот счет поднять в несколько раз давление газа по сравнению с классическим тлеющим разрядом.
При наличии внешней ионизации могут реализовываться две разновидности разряда. Одна из них называется несамостоятельным разрядом, непрерывный источник ионизует среду, в которой протекает основной разряд. Но как только прекращается внешняя ионизация, так тут же прекращается горение основного разряда, он самостоятельно существовать не может. Вторая разновидность – самостоятельный разряд, он может существовать и без непрерывной вспомогательной ионизации, роль которой ограничивается созданием только начальной ионизации и последующей помощи в некотором снижении напряженности поля.
Создание непрерывных СО2 лазеров с ионизацией вспомогательным разрядом оказалось весьма непростой задачей. Дело в том, что увеличить мощность вспомогательного разряда можно только до определенного предела, выше которого этот разряд начинает выделять слишком много тепла. Кроме того, вспомогательный разряд должен быть диффузного типа, что существенно уменьшает возможности выбора. Чаще всего используется вспомогательный ВЧ разряд. Наилучшие результаты, достигнутые в таком варианте, позволили поднять давление наполняющего газа примерно до 150 Тор. Такие лазеры с предельной мощностью до 10 кВт широко используют в лазерных станках для обработки материалов.
Ионизация активной среды пучком быстрых электронов. Источником быстрых электронов служит электронная пушка, схематично изображенная на рис. 2.18.
Мощный подогревный катод, источник быстрых электронов, находится под потенциалом от -250 до -400 кВ. Анод, выполняющий одновременно и функцию переходного узла от пушки к лазерной камере, представляет собой решетку из нержавеющей стали, герметично закрытую достаточно тонкой, но прочной алюминиевой, титановой или другой подобной фольгой толщиной от 20 до 40 мкм. Пространство между катодом и анодом откачено до высокого вакуума при остаточном давлении воздуха не выше 10–6 Тор. Такое давление поддерживается непрерывной работой откачной системы, состоящей из форвакуумного и одного – двух мощных диффузионных насосов. Пушка пристыковывается к лазерной разрядной камере, отделяясь от нее анодной решеткой плотно закрытой фольгой. Эмитируемые катодом пушки электроны ускоряются в промежутке катод – анод, и через отверстия в анодной решетке и фольгу проникают в разрядную камеру. Энергия электронов достигает нескольких сотен эВ, они ионизуют активную среду. Приложенного к электродам напряжения недостаточно для инициации и поддержания разряда без внешней ионизации, это типичный несамостоятельный разряд. Напряженность поля составляет 2 – 4 кВ/см вместо 8 – 10 кВ/см в самостоятельном разряде. Такие параметры создают наиболее благоприятные условия для избирательного заселения верхнего лазерного уровня. Лазеры, использующие пучок быстрых электронов в качестве источника ионизации, иногда в технической литературе называют электроионизационными.
Достоинства непрерывного электроионизационного лазера: 1) возможность организации тлеющего разряда при давлениях активной смеси порядка 1 атм (в условиях непрерывной прокачки газа); 2) возможность задействования больших объемов активной среды за счет существенного увеличения поперечного сечения разрядной области (межэлектродное расстояние достигает 50 см); 3) возможность модулировать разряд путем модуляции электронного пучка; 4) возможность работать при оптимальных с точки зрения накачки параметрах несамостоятельного разряда.
Недостатки электроионизационных лазеров: 1) сравнительно короткий срок службы электронной пушки, что связано с выходом из строя подогревного катода; 2) уязвимость фольгового узла, возможности электрического пробоя фольги, что ведет к попаданию газа из камеры в пушку и сопровождается полным ее выходом из строя; 3) применение сложных высокопроизводительных вакуумных насосов создает еще один узел потенциального отказа техники; 4) необходимость использования мощной биологической защиты персонала от рентгеновского излучения, сопровождающего работу установки; 5) сложность эксплуатации и настройки всей системы, высокая стоимость, как самой установки, так и ее эксплуатации. Перечисленные недостатки не позволяют широко использовать электроионизационные лазеры в промышленных целях.
Проблема распада (диссоциации) молекул СО2 является достаточно серьезной, так как в условиях замкнутой прокачки такое явление ведет к снижению со временем выходной мощности лазера. Ни молекула СО2 , ни молекула N2 не диссоциируют термическим путем. Температура газа в разряде составляет доли эВ, в то время как энергия разрыва химической связи одного атома кислорода молекулы СО2 составляет 5,47 эВ, а энергия разрыва двух атомов кислорода, то есть полного распада молекулы СО2 , составляет 9,75 эВ. Диссоциация молекул в тлеющем разряде происходит либо в результате прямого удара достаточно быстрого электрона
(2.62)либо в результате диссоциативной рекомбинации:
(2.63)Преобладает в разряде процесс (2.62), так как скорость его протекания пропорциональна произведению ne.nа, в то время как скорость диссоциативной рекомбинации пропорциональна лишь nе2.
Обратные процессы, ведущие к восстановлению молекул СО2 в разряде, могут протекать либо в объеме, при тройных столкновениях с молекулами газа Х:
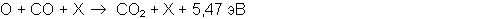
(2.64)либо на стенках камеры при условии, что они поглощают образующийся в разряде кислород
(2.65)В стационарном состоянии устанавливается динамическое равновесие:
(2.66)и относительное содержание СО2 , СО и О2 в разряде определяется особенностями разрядной трубки (камеры). Например, в зависимости от типа используемого катода или от материала стенок реакция (2.66) может сдвигаться как вправо, так и влево. Восстановлению молекул СО2 способствует добавка в активную среду небольшого количества водорода. Разложение молекул СО2 активируется ростом температуры и увеличением силы разрядного тока.
От степени диссоциации исходного количества молекул СО2 зависит инверсная населенность, а с ней и генерируемая лазером мощность. Экспериментальная зависимость
от степени диссоциации при протекании разряда в смеси СО2 : N2 : He = 1:3:6 при общем давлении 7 Тор и при температуре 400 К представлена в качестве примера на рис. 2.19.
При степени диссоциации до 20% наблюдается некоторый подъем инверсной населенности. Он вызван тем, что в небольшом количестве молекулы СО передают свою энергию возбуждения молекулам СО2 , резонансно заселяя верхний лазерный уровень 00о1, как это делает молекула азота. Затем начинает сказываться убыль молекул СО2 и, соответственно, падение инверсной населенности. Примерно такой же характер имеет зависимость
от времени пребывания смеси в разряде при осуществлении протока газа. Чем интенсивнее протекает диссоциация молекул СО2 , тем быстрее следует прокачивать рабочую смесь через зону разряда, чтобы не допустить снижения выходной мощности лазера.
Развитие мощных импульсных СО2 лазеров началось после того, как в конце 1969 года двумя группами исследователей, одна – в Канаде, другая – во Франции, была реализована идея разделения процессов ионизации и возбуждения молекул в тлеющем разряде. В отличие от режима непрерывной генерации, в случае импульсных лазеров достаточным оказалось осуществить предионизацию разрядного промежутка, не заботясь о дальнейшем. Обе группы использовали для предионизации вспомогательный разряд, с некоторым опережением ионизующий разрядный промежуток перед тем, как в нем возникнет основной разряд. Но без такой предионизации основной разряд возникнуть не может, поскольку приложенного к электродам напряжения недостаточно для пробоя разрядного промежутка. Импульсные лазеры с вспомогательным разрядом получили в англоязычной литературе название TEA лазеров. Аббревиатура расшифровывается так: transversally excited at atmospheric pressure (поперечное возбуждение при атмосферном давлении).
Импульсные лазерные системы проще, чем непрерывные, решают проблему генерации высокоэнергичных импульсов излучения, поскольку длительность импульсов, как правило, намного короче времени развития тепловых процессов в активной среде. Все это вместе с высоким к.п.д., присущим СО2 лазерам, позволило достичь в таких системах энергий в импульсе до нескольких сотен килоджоулей. Кроме газоразрядных, или ТЕА лазеров, создана и другая их разновидность – электроионизационные импульсные лазеры, в которых ионизация осуществляется электронным пучком, а разряд, соответственно, является несамостоятельным.
Системы газоразрядной предионизации. Главное требование к системам газоразрядной предионизации – возможность с их помощью создать в активной среде такую степень начальной ионизации, которая обеспечит последующее развитие основного разряда при значениях Е/р, наиболее благоприятных для избирательного возбуждения верхнего лазерного уровня 00o1 молекулы СО2. Концентрация электронов, удовлетворяющая такому условию, лежит в пределах от 108 до 1011 см–3, но желательно сделать ее как можно ближе к верхнему значению. В процессе протекания основного разряда предионизатор участия не принимает. Наибольшее распространение получили предионизаторы, использующие вспомогательный разряд одного из следующих типов.
Коронный разряд обычно образуется между острием или тонкой проволокой, находящимися под высоким напряжением, и заземленным электродом. Коронный разряд неравновесен, при холодном газе электронная температура достигает нескольких электрон-вольт. Такой разряд интенсивно излучает в УФ области спектра, вызывая фотоионизацию газа. Упрощенно устройство лазера с предионизацией коронным разрядом показано на рис. 2.20.
С обеих сторон разрядного промежутка параллельно основным электродам натянуты две тонкие проволочки, обозначенные на рисунке КР. К основным электродам подведено напряжение более низкое, чем необходимо для пробоя разрядного промежутка. Напряжение между проволочками и заземленным основным электродом достаточно для развития с каждой стороны промежутка коронного разряда. Создаваемое при этом УФ излучение ионизует разрядный промежуток, и в нем развивается основной разряд, обеспечивающий возникновение импульсной лазерной генерации. От системы предионизации требуют организации высокой однородности начальной концентрации электронов в разрядном промежутке. Это необходимо для получения стабильного и эффективного основного разряда при атмосферном давлении газовой смеси. Предионизационная система, использующая коронный разряд, создает однородную ионизацию только при относительно малых поперечных сечениях разрядного промежутка, поскольку ультрафиолетовое излучение активно поглощается в газе и при больших сечениях центральные области разрядного промежутка оказываются непроработанными. Это накладывает серьезные ограничения на применение таких систем.
Множественные искровые разряды. Предионизатор такого типа широко используется во многих лазерных системах средней мощности. Система множественных искровых разрядов создана Ричардсоном в 1973 году. На рис.2.21 приведена электрическая схема предионизатора этого типа.
Анод основного разрядного промежутка выполнен в виде сетки из нержавеющей стали, натянутой между изоляторами. Под сеткой расположены игольчатые электроды, например, в 6 рядов по 100 иголок в каждом ряду. Основной разряд формируется с использованием высоковольтной импульсной системы питания, работающей на базе двухкаскадного генератора Маркса с удвоением напряжения источника питания. Накопительные емкости С s = 0,1 мкФ заряжаются от высоковольтного выпрямителя до номинального напряжения. Триггерный разрядник Р1 после подачи на его управляющий электрод запускающего импульса пробивается и переключает конденсаторы Сs из параллельного в последовательное соединение. В результате неуправляемые разрядники Р2 и Р3 оказываются под удвоенным напряжением, вызывающим их пробой и подведение напряжения к основным электродам и к вспомогательному разрядному промежутку между иголками и анодом. Подведенного напряжения недостаточно, чтобы пробить основной разрядный промежуток, но хватает для появления множественных искровых разрядов между иголками и анодом. Искровые разряды создают интенсивное УФ излучение, производящее фотоионизацию разрядного промежутка. Если уровень ионизации будет достаточно высоким, то в основном промежутке лавинообразно протекает импульс основного разряда между катодом и анодом. Тем самым создаются условия для проявления лазерного эффекта. При участии такой системы предионизации удается вложить в активную среду энергию, превышающую 300 Дж/л. А так как к.п.д. преобразования вложенной энергии в лазерное излучение в среднем составляет 10%, то активная среда генерирует излучение на уровне 30 Дж/л.
Предионизация барьерным разрядом. Барьерным называют разряд, который протекает через диэлектрик за счет токов смещения. Такая форма разряда может существовать только в режиме коротких импульсов. Один из вариантов схемы предионизации барьерным разрядом представлен на рис. 2.22 [8].
Основной разрядный промежуток расположен между катодом (К) и анодом (А). В устройстве, рассматриваемом на рисунке, анод и катод представляют собой дюралюминиевые пластины. В теле катода фрезеруются поперечные пазы, в которые уложен тонкий провод в надежной изоляции (пи).
Источник питания заряжает накопительные емкости С1 и С2, которые первоначально соединены параллельно. Подача на триггерный разрядник Р1 запускающего импульса напряжения вызывает пробой разрядника, что ведет к переключению емкостей из параллельного в последовательное соединение. Это двухкаскадная схема Маркса. Напряжение на накопительной батарее удваивается, и это приводит к пробою неуправляемого разрядника Р2. В результате между анодом и катодом появляется напряжение, но его величина недостаточна для пробоя газа в разрядном промежутке. Однако через разделительную емкость С3 то же напряжение прикладывается между вспомогательным проводом (пи) и катодом. Через изоляцию провода проходит ток смещения, и над катодом возникает диффузный разряд, создающий ультрафиолетовое излучение, способное осуществить фотоионизацию разрядного промежутка. Это и есть разряд барьерного типа, он как бы покрывает собой всю поверхность катода. Длительность такого разряда не превышает десятков наносекунд, но этого достаточно, чтобы создать необходимую начальную ионизацию. Тогда напряжение, приложенное к основным электродам, оказывается достаточным, чтобы вызвать протекание разрядного тока в ионизованном основном промежутке, и произвести импульс накачки активной среды.
Описанная система предионизации оказалась эффективной, с ней получены съемы когерентного излучения от 30 до 50 Дж/см3 при к.п.д. до 15%. Для повышения эффективности предионизации в рабочую газовую смесь вводились в виде небольших добавок легкоионизуемые вещества [8,9]. Для предионизации активной среды импульсных СО2 лазеров используются также и некоторые другие виды вспомогательных разрядов, например, поверхностные разряды на диэлектрике, но они не получили широкого распространения.
В импульсном разряде выделяются три стадии. Первую стадию назовем переходной стадией в развитии импульсного разряда, вторую – основной стадией, и ее перекрывает третья стадия, во время которой происходит генерация лазерного излучения. Рассмотрим особенности каждой стадии.
Переходная стадия в развитии импульсного разряда с предионизацией. Создаваемая вспомогательным разрядом начальная концентрация электронов достаточна для пропускания тока через пространство между основными электродами, но не достаточна для вложения в образовавшуюся плазму необходимой энергии накачки. Поэтому сразу после включения основного разряда проходит некоторое время, в течение которого процессы ионизации в основном разряде увеличивают электронную концентрацию до величины, достаточной для эффективного образования инверсной населенности между верхним и нижним лазерными уровнями. Достижение этой цели требует несколько более высокого значения напряженности электрического поля в разрядном промежутке Е/р, чем необходимо для эффективного избирательного возбуждения верхнего лазерного уровня.
Расчеты, подтверждаемые экспериментальными данными, показывают, что для достижения за время импульса нужной концентрации электронов, их начальная концентрация neo должна быть не ниже определенного критического уровня, равного примерно 108 см-3. На практике чем выше это значение, то есть чем мощнее предионизация, тем эффективнее работает импульсный лазер. Следовательно, к системе предионизации предъявляются очень жесткие требования. В устойчиво работающих импульсных лазерах предионизационный разряд создает начальную концентрацию электронов не ниже 109 см-3. Для развития последующей ионизации и для эффективной накачки верхнего лазерного уровня молекул СО2 в смеси СО2 – N2 – He необходимо, чтобы значение параметра Е/р у основного разряда превышало 45 В/см.Тор. Например, в лазерах, работающих при атмосферном давлении наполняющих газов, напряженность электрического поля Е лежит в пределах от 5 до 10 кВ/см.
Превышение этого уровня порождает неустойчивость разряда. Параметры, обеспечивающие эффективную генерацию лазерного излучения электроразрядным импульсным СО2 лазером при атмосферном давлении газов, ограничены узкими рамками приемлемых значений.
Особенности развития основного разряда в системе с предионизацией вспомогательным разрядом рассмотрим на конкретном примере [8]. На рис.2.23 приведены осциллограммы напряжения, тока и плотности мощности выходного излучения ТЕА лазера с предионизацией барьерным разрядом по схеме рис. 2.22.
Как видно из осциллограмм, разрядный ток появляется через 4 мкс после срабатывания триггерного разрядника и подачи напряжения на разрядный промежуток. Задержка определяется временем формирования вспомогательного барьерного разряда и создания им начальной ионизации среды. За это время рост напряжения на основном разрядном промежутке должен обеспечить достижение такого его значения, которое создаст ускорение электронов в среде, достаточное для развития необходимого уровня ионизационного процесса в самом разряде. Ток возникает после того, как напряженность электрического поля в разрядном промежутке достигнет значения Е = U/d
8 кВ/см. Здесь d – расстояние между электродами. Временной интервал между включением напряжения и появлением тока условимся называть предварительной стадией развития импульсного разряда.
С момента появления разрядного тока начинается основная стадия разряда. Она завершается с прекращением тока. Из осциллограммы тока на рис. 2.23 в данном примере она заканчивается на 9-й микросекунде, ее продолжительность – 5 микросекунд. Прекращение тока вызвано снижением напряженности электрического поля до предельного значения порядка 5 кВ/см. Плотность разрядного тока определяется соотношением:
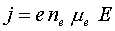
где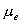
– подвижность электронов в газовой смеси. Снижение Е сопровождается снижением как подвижности, так и концентрации электронов. Протекание тока становится невозможным, как только обе эти величины снижаются вместе с напряженностью поля до критического уровня.
На основной стадии разряда в каждый момент времени концентрация электронов определяется из уравнения непрерывности:
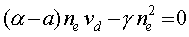
(2.67)
где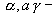 
соответственно коэффициенты ионизации, прилипания и рекомбинации; 
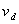– скорость дрейфа электронов в электрическом поле (
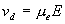). Из (2.67) следует:
и 
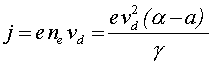
(2.68) Величины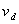
, 
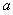, называют коэффициентами переноса, расчетные методы их определения рассматриваются в курсе физики плазмы.
К соотношениям (2.67) и (2.68) добавляют соотношение, определяющее среднюю энергию электронов:
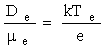
где De – коэффициент диффузии электронов. Совместное решение всех записанных уравнений позволяет определить из соотношения (2.68) вольтамперную характеристику разряда, а при известном законе зависимости Е/р от времени описать форму импульса тока, энергию накачки и некоторые другие характеристики импульсного разряда.
Из осциллограмм рис.2.23 видно, что генерация лазерного импульса начинается не вместе с токовым импульсом, а с некоторым запозданием. Конкретно в приводившемся примере это запаздывание составляло 2 мкс. Возникшая генерация продолжается и некоторое время спустя после завершения токового импульса. На осциллограмме последействие составляет примерно 1 мкс. Период протекания лазерного излучения можно считать третьей стадией развития разряда, причем она перекрывается с основной стадией и характеризуется распадом плазмы в результате прекращения поступления энергии извне.
Основные элементы ТЕА лазера. Типичный импульсный электроразрядный (ТЕА) СО2 лазер состоит из элементов, показанных на блок-схеме рис. 2.24.
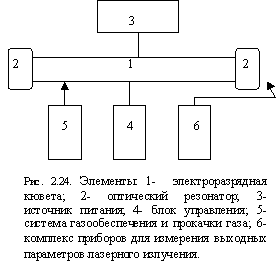
При всем разнообразии в устройстве каждого такого элемента, общая схема остается практически неизменной. В качестве примера продолжу рассмотрение описанного выше ТЕА лазера, обладающего высокими выходными характеристиками [8]. Так, при длительности импульса генерации от 2-х до 4-х мкс энергия в импульсе достигает 800 Дж.
Кювета и электроды. Герметичная газоразрядная кювета (1) изготовлена из стеклопластика. Кювета может быть изготовлена и из других диэлектрических материалов, например, из специальных пластмасс, в некоторых случаях ее изготавливают из металла. Но металлическая кювета требует создания на ее внутренних стенках прочного изоляционного покрытия, способного противостоять напряжениям порядка сотни кВ. Кроме того, металлическая кювета требует применения громоздких проходных изоляторов, обеспечивающих подачу высоковольтного напряжения от источника питания на электроды. Диэлектрическая кювета снимает эти усложняющие конструктивные проблемы.
В рассматриваемом лазере размеры кюветы: поперечное сечение квадратное, размер сторон 30см; длина 2,3 м. Внутри кюветы на ее верхней и нижней стенках закрепляется секционированная электродная система. Электроды разделены на 4 секции, каждая секция состоит из катода в виде дюралюминиевой пластины размером по ширине 150 мм и по длине 400мм, и противостоящего анода также в виде дюралюминиевой пластины несколько большего размера, чем катод. Вспомогательный электрод для предионизации, обеспечивающий протекание разряда барьерного типа, представляет собой провод в электрически прочной, но тонкой изоляции, он уложен зигзагообразно в поперечных пазах, выфрезерованных в катодной пластине. Диаметр металлической жилы провода 0,5 мм, диаметр провода с изоляцией 2,5 мм. Секции расположены последовательно внутри кюветы и отделены друг от друга небольшими промежутками, исключающими пробой между ними. Питающее напряжение подводится к каждому электроду через компактные проходные изоляторы.
При работе в режиме одиночных импульсов нет необходимости в прокачке газа через разрядный промежуток, поскольку тепловые процессы развиваются уже после того, как завершен разрядный импульс. Активная часть объема кюветы состоит из суммы объемов разрядных зон каждой секции, она составляет 16 л. Общий объем внутренней полости кюветы, заполняемый газовой смесью, в 3-4 раза превышает активный объем. Это позволяет длительное время компенсировать протекающий в разряде процесс диссоциации молекул СО 2 , восполняя потери за счет запаса свежего газа. В результате удается осуществить около сотни импульсов генерации, прежде чем выходная мощность излучения снизится более чем на 10% от исходных значений. После этого производится смена газовой смеси в кювете. При желании работать в частотно-импульсном режиме, необходимо осуществлять прокачку газа. Для этого на боковых стенках кюветы имеются широкие окна, к которым пристыковывается газодинамический прокачной тракт. Торцы кюветы герметично закрываются юстировочными блоками, внутри которых установлены зеркала оптического резонатора.
Оптический резонатор. В описываемом лазере применен устойчивый оптический резонатор. Зеркала резонатора установлены в торцевых юстируемых фланцах. Выбран резонатор полуфокального типа, одно из зеркал имеет отражающую поверхность сферической формы, второе зеркало – плоскопараллельное. Медное сферическое зеркало диаметром 180 мм имеет радиус кривизны от 20 до 40 м. Оно изготавливается алмазным точением, после которого нет необходимости производить полировку поверхности. На противоположном конце располагается полупрозрачное выходное зеркало, изготовляемое из монокристалла германия. Диаметр зеркала 160 мм при толщине 25 мм. Обе рабочие поверхности германиевой пластины подвергаются обработке по специальной технологии, обеспечивающей их высокое оптическое качество. Наружная грань пластины имеет напыленное просветляющее покрытие. На длине волны 10,6 мкм коэффициент отражения зеркала равен 0,36, соответственно коэффициент пропускания равен 0,64. Германиевая пластина выдерживает поверхностные лучевые нагрузки, не превышающие примерно 10 Дж/см2 Поскольку сечение генерируемого луча представляет собой квадрат со стороной 100 мм, то зеркало позволяет выводить лазерное излучение с общей энергией в импульсе не более 1 кДж.
Источник электропитания. Первичный источник электропитания – стандартная сеть напряжением 220 или 380 В. Далее следуют такие элементы:
1) регулятор напряжения; 2) высоковольтный трансформатор; 3) высоковольтный выпрямитель; 4) блок формирования и коммутирования импульса электропитания (БФИ); 5) элементы цепи питания.
Центральный элемент схемы – БФИ. Поскольку электродная система разделена на четыре независимые секции, то и БФИ разделен на такое же число секций, каждая из которых собрана по схеме, представленной на рис.2.22. Каждая секция питания подключена к одной электродной секции. Секционированное электропитание вместе с секционированной электродной системой позволяет, во-первых, существенно снизить токовые нагрузки на элементы БФИ; во-вторых, использовать различные варианты совместного или раздельного запуска секций, что расширяет возможности использования лазера. Например, при работе на пониженных энергиях в импульсе нет необходимости использовать все секции лазера, можно включить только одну, или две, или три секции в соответствии с потребностью. Запуская секции не совместно, а поодиночке с некоторым интервалом, можно создавать пакеты импульсов от 2-х до 4-х. Конечно, при этом энергия в каждом импульсе существенно ниже, чем при синхронном запуске всех секций. Серьезная проблема, возникающая при проектировании БФИ, состоит в возможностях комплектования схемы накопительными конденсаторами и высоковольтными разрядниками. В рассматриваемой схеме, в частности, использованы малоиндуктивные конденсаторы на напряжение 100 кВ, емкость которых С1 = С2 = 0,5 мкФ. Конденсаторы такого типа стоят дорого и создают трудности, связанные с их габаритами и весами. Дополнительная проблема возникает при необходимости работы в частотно-импульсном режиме, так как возможности конденсаторов работать при частотах повторения импульсов ограничены. При частотах, превышающих несколько герц, накопительные батареи заменяются специальными модулирующими устройствами, что усложняет источник питания. Подробно эти вопросы рассматриваются в литературе, посвященной мощным импульсным источникам питания. Что же касается управляемого (Р1) и неуправляемого (Р2) разрядников, то при работе в режиме одиночных импульсов успешно используются открытые воздушные разрядники специальной конструкции. При этом обеспечивается точность синхронного срабатывания разрядников всех четырех секций на уровне наносекунд. Более надежными считают разрядники закрытого типа, наполняемые азотом до давлений в несколько атмосфер.
Газоснабжение кюветы включает:
1) блок откачки отработанной газовой смеси: с этой задачей успешно справляется производительный форвакуумный насос;
2) баллоны, наполненные газами, необходимыми для создания рабочей смеси (СО2 , N2, He);
3) специальную емкость для приготовления смеси газов с заданными парциальными давлениями компонентов, откуда смесь вводится в кювету. В лабораторных условиях напуск газов с нужными парциальными давлениями может производиться прямо в кювету из баллонов;
4) блок ввода в кювету органической присадки при парциальном давлении на уровне 1 тор;
5) газовые магистрали, дистанционно управляемые клапаны, точные манометры.
После откачки отработанной газовой смеси и перед наполнением свежей смесью, кювету необходимо промыть азотом.
Измерение выходных параметров лазерного луча. Необходимо обеспечить измерение энергии излучения и формы лазерного импульса в каждом генерируемом импульсе. Для этого применяют схему, изображенную на рис. 2.25.
Луч лазера по выходе из оптического резонатора проходит через оптический клин (2), прозрачный для излучения в области длин волн от 9 до 11 мкм. Для этого клин изготавливается, например, из монокристалла NaCl. Около 4% энергии отражается от передней грани клина и попадает в калориметрический измеритель энергии (3). Энергия, отражающаяся от задней грани клина, попадает на вход германиевого фотоприемника (5), временное разрешение которого не хуже, чем 10-9с. Развернутый во времени сигнал приемника фиксируется на экране осциллографа (6), он представляет ход изменения интенсивности луча во времени. В случае необходимости с применением стандартной процедуры измеряется расходимость лазерного луча. При создании лазерного станка данные о параметрах луча поступают в блок управления и автоматически учитываются при обеспечении заданного режима генерации.
Электроионизационные импульсные и частотно-импульсные лазеры. По внешнему виду импульсные электроионизационные лазеры не отличаются от непрерывных лазеров соответствующего уровня мощности. Но некоторые их элементы существенно различаются. Электронная пушка импульсного лазера должна обеспечивать образование очень мощных кратковременных электронных пучков с энергиями 100 – 300 кэВ. Для этого катод такой пушки должен обладать способностью почти мгновенного создания мощного токового импульса. Термоэмиссионный катод не способен работать в таком режиме, поэтому используется либо катод с автоэлектронной эмиссией, либо катод с эмиссией взрывного типа, выдерживающие подобные нагрузки. Катод и электронная пушка в целом остаются одним из наименее надежных элементов системы.
Электронный пучок, вводимый в разрядный объем кюветы, ионизует молекулы газа, а приложенное к основным электродам напряжение от модулятора создает в ионизованной среде импульсный разряд несамостоятельного типа. Успешная работа лазера зависит от того, способна ли активная среда воспринять необходимую энергию накачки за короткий промежуток времени.
Поскольку импульсные электроионизационные лазеры обладают теми же недостатками, что и непрерывные лазеры такого типа, их использование в лазерных станках, как правило, оказывается неприемлемым. Прежде всего по причине необходимости создания мощной биологической защиты от сильного рентгеновского излучения, сопровождающего их функционирование. В производственных условиях это недопустимо.
Емкость конденсаторной батареи. Энергия Wk, запасаемая конденсаторной батареей, равна:
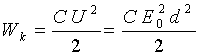
(2.69)где С – емкость конденсаторной батареи, Е0 – начальная напряженность электрического поля при зарядке батареи, d – расстояние между основными электродами лазера. После предионизационной подготовки в разрядном промежутке появляется исходная концентрация электронов, что ведет к пробою промежутка и введению в него энергии от разряжающейся конденсаторной батареи. Используя уравнение Кирхгофа для малоиндуктивного контура с включенной в него батареей конденсаторов, получают выражение для энергии Wp, передаваемой в разрядный промежуток:
,
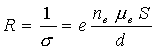
(2.70) здесь S – площадь электродных пластин, tn – длительность разрядного импульса, 
- электропроводность плазмы, R – сопротивление плазмы электрическому току, 
- подвижность электронов, е – заряд электрона.
Введем в (2.70) обозначение:
(2.71) Число (1 ? К) определяет введенную в разряд долю энергии, запасенной в конденсаторной батарее. Если число К близко к единице, то в разряд переходит незначительная часть запасенной энергии, и к.п.д. лазера будет низким. Если же К очень мало, то есть батарея почти полностью разряжается, то в процессе протекания разряда будет существенно меняться напряженность электрического поля Е, в результате чего на значительном протяжении токового импульса напряженность поля оказывается далекой от оптимального значения с точки зрения возбуждения молекул азота и СО2 . Соответственно упадет энергия в излучаемом импульсе и снизится к.п.д. лазера. Наиболее выгодными для эффективной работы лазера считаются значения К в интервале от 0,5 до 0,7. Емкость конденсаторной батареи, необходимой для введения в разряд оптимальной энергии, можно определить из соотношения (2.70), если учесть оптимальное значение К, начальную концентрацию электронов в разрядном промежутке 
, и коэффициент рекомбинации молекул с электронами 
:
(2.72)При бесконечном увеличении емкости количество вводимой в разряд энергии достигает конечного предела:
(2.73)
Оптические элементы мощных лазеров. Непременной частью любого лазера и связанных с ним устройств являются оптические элементы. Когда рассматриваются СО2 лазеры, генерирующие излучение на длинах волн от 9 до 11 мкм, непременным требованием к оптическим элементам выступает их совместимость с этим диапазоном. Кроме того, поскольку речь идет о мощных лазерах, то появляется еще одно требование к оптическим элементам – высокая лучевая стойкость.
Различные оптические элементы, используемые в лазерных установках, можно разделить на четыре группы: 1) элементы резонатора; 2) выходные окна генераторов или усилителей; 3) оптические элементы внешней схемы лазерной установки; 4) нелинейные оптические элементы (затворы, модуляторы, преобразователи длины волны и другие). Последнюю группу здесь рассматривать не будем, она занимает особое положение.
Элементы оптического резонатора ? это зеркала. Они бывают либо полностью непрозрачными («глухие»), либо частично прозрачными (выходное зеркало). Глухие зеркала изготавливаются из металла (чаще всего это медь) или из специальной подложки, на которую напыляется слой, отражающий не менее 95% падающего излучения. Подложка в этом случае выбирается такой, чтобы она способствовала интенсивному охлаждению отражающего слоя. Выходные зеркала для СО2 лазеров изготавливаются из монокристаллов, пропускающих определенную часть излучения на длине волны этого лазера и отражающих почти всю остальную часть излучения. Как правило, для задания нужных коэффициентов пропускания и отражения, на поверхности пластины из монокристалла напыляют либо просветляющие, либо отражающие интерференционные покрытия.
Различают оптические резонаторы устойчивой и неустойчивой конфигураций. Схематично они изображены на рис.2.26.
Выходное зеркало устойчивого резонатора частично прозрачно для излучения на длине волны лазера. Отражающая поверхность и материал зеркала должны обладать минимальными потерями на поглощение. Сечение выходящего луча зависит от конфигурации разрядного промежутка и от формы выходной апертуры. На рисунке, в частности, изображено квадратное сечение луча. Квадрат при хорошем качестве зеркал и однородности разряда равномерно заполнен излучением, за исключением краев, где происходит спад интенсивности.
В случае неустойчивого резонатора (Б) оба зеркала «глухие». Заднее зеркало обычно имеет вогнутую сферическую отражающую поверхность, а переднее выходное зеркало – выпуклую поверхность. Выходное зеркало затеняет всю центральную часть луча, и его сечение имеет форму «бублика». Несмотря на неудобства, связанные с особой формой сечения луча, неустойчивые резонаторы широко применяются в мощных лазерах. Одна из причин – высокая лучевая стойкость металлических зеркал.
В мою задачу не входит изложение теории и практики исполнения оптических резонаторов, этим вопросам посвящены многочисленные специальные учебники и монографии. Ограничусь рассмотрением тех кристаллических материалов, которые используются для создания зеркал, частично прозрачных в инфракрасном диапазоне длин волн.
Выходные окна лазеров и усилителей. Их назначение – герметично закрывать торцы кюветы и при этом пропускать излучение на лазерной длине волны. Выходные окна ? обязательный элемент усилителей. В лазерных генераторах их используют в двух случаях: когда по каким-то причинам устанавливается оптический резонатор с выносными зеркалами, или когда применен неустойчивый оптический резонатор. Торцы кюветы лазера с устойчивым резонатором герметично закрываются фланцами, в которых установлены с одного конца глухое, а с противоположного – выходное зеркала.
Оптические элементы внешней схемы. Такие элементы предназначаются для формирования лазерного луча, для его расщепления (при необходимости), для направления на нужный объект и частично на измерительные приборы. В качестве примера небольшого участка внешней схемы можно рассмотреть рис.2.28, где с помощью оптического клина и глухих поворотных зеркал небольшая часть излучения направляется на измеритель мощности и измеритель интенсивности луча. В общем случае добавляются линзы, призмы, поляризаторы и другие необходимые оптические элементы.
Материалы для элементов ИК-оптики. Все оптические элементы по своему назначению разделяются на три группы. Первую группу составляют элементы, назначение которых – отражать излучение при минимальном его поглощении и рассеянии. Назначение элементов второй группы – частично отражать и частично пропускать излучение заданной длины волны опять же при минимальном поглощении. Предназначение элементов третьей группы – пропускать излучение заданной длины волны при минимальных значениях отражения и поглощения.
Отражающие элементы. К этой группе относятся «глухие» зеркала. Чаще всего для их изготовления используют медь, специальные бронзы, реже алюминий. Отражающие поверхности обрабатываются на оптических станках, где поверхности придается точная заданная форма – плоскость, сфера заданного радиуса кривизны, эллиптическая или параболическая поверхность. После механической обработки отражающая поверхность подвергается шлифовке и полировке. В последние годы начали широко применять чистовую обработку поверхностей с применением алмазного инструмента (алмазное точение). Такая обработка делает ненужными процессы шлифования и полирования. Для повышения отражательной способности поверхности и защиты ее от окисления иногда напыляется тончайший слой золота. Кроме металлов зеркала изготовляют на основе пористых диэлектриков или композитных материалов с напылением на рабочую поверхность диэлектрических отражающих покрытий. Такие зеркала эффективно охлаждаются водой (с тыльной стороны). Тем самым удается существенно повысить предельные лучевые нагрузки на отражающую поверхность. Удается достигнуть у высококачественных зеркал коэффициента отражения на длине волны лазерного излучения от 0,99 до 0,999.
Прозрачные и частично прозрачные оптические элементы для ИК области спектра изготавливаются на основе аморфных или кристаллических диэлектриков. Для длины волны СО2 лазеров непригодны оптические стекла и ситаллы, они поглощают такое излучение в тонком поверхностном слое. Нужными свойствами обладают материалы, принадлежащие к одной из следующих трех групп: 1) ионные монокристаллы; 2) полупроводниковые кристаллы; 3) халькогенидные стекла и оптическая керамика. Данные о некоторых представителях таких материалов приведены в таблицах 2.6 – 2.8.
Список материалов, прозрачных в области спектра от 9 до 11 мкм, можно расширить. Но прозрачность – это только первая составляющая в комплекте условий, определяющих пригодность материала для изготовления из него оптических элементов, особенно когда речь идет о мощных СО2 лазерах. Так, специалисты признают, что по всем своим характеристикам алмаз – самый лучший материал для выходных окон. Но изготовить алмазные пластины необходимых для этих целей размеров, не говоря уж об их стоимости, если бы такое стало возможным, в обозримом будущем нереально. Другой пример. На протяжении многих лет велись работы по получению КРС нужных размеров и кондиции. На эти исследования возлагались серьезные надежды и были достигнуты значительные успехи. Однако, КРС слишком мягок и пластичен, его поверхность трудно довести до нужного оптического качества. Со временем изготовленный из КРС элемент пластически деформируется. Ко всему сказанному добавляется еще одна неприятность – в основе материала заложены мышьяковистые соединения, что делает его чрезвычайно токсичным. Отсюда видно, что конструктивные и экологические требования к материалу накладывают серьезные ограничения на возможности его применения в лазерных установках.
Окно закрывает торец разрядной камеры и выполняет при этом не только оптические, но и конструкционные функции, что вносит дополнительные требования к прочности материала, к выбираемой толщине окна.
Основная проблема зеркал и выходных окон мощных лазеров определяется неизбежным взаимодействием интенсивного когерентного излучения с поверхностями и объемом этих оптических элементов. В этой связи выбираемые для их изготовления материалы должны удовлетворять дополнительным требованиям:
- обладать как можно лучшими теплофизическими свойствами, а именно, иметь высокий коэффициент теплопроводности, высокую температуру плавления и низкий коэффициент линейного расширения;
- оптические свойства материала не должны зависеть от рабочей температуры;
- обладать минимальным коэффициентом поглощения на лазерной длине волны
- в объеме и на поверхности материала не должны присутствовать непрозрачные включения;
- иметь низкие значения фотоупругих констант.
К этим требованиям добавляют: устойчивость к воздействию внешней среды и рабочего вещества лазера; малый показатель преломления. Желательна прозрачность материала в видимой области спектра, что облегчает юстировку, и по возможности, дешевизна и технологическая простота изготовления и оптической обработки.
Материалов с перечисленными свойствами в природе не существует. Поэтому выбор подходящего материала – это всегда разумный компромисс между идеальными требованиями и реальными возможностями при детальном учете условий, в которых изделие должно работать.
К разделу 1
1. Звелото О. Принципы лазеров. М.: Мир, 1990
Orazio Sveloto, Principles of Lasers. Third Edition. Plenum Press – New York and London
2. Карлов Н.В. Лекции по квантовой электронике. М.: Наука, 1988
К разделу 2
3. Райзер Ю.П. Физика газового разряда. М.: Наука, 1987
4. Шкаровский И., Джонстон Т., Бачинский М. Кинетика частиц плазмы.
М.: Атомиздат,
1969
Shkarofsky I., Johnston T., Bachynski. The Particle Kinetics of Plasmas.
Addison-Wesley
Publishing Co. Reading, Massachusetts - Palo Alto – London – Don Mills, Ontario 1966
5. Голант В.Е., Жилинский А.П., Сахаров С.А. Основы физики плазмы,
М. Атомиздат,1977
6. Грановский В.Л. Электрический ток в газе.
М.: Наука, 1971
7. Газовые лазеры.
Новосибирск, Наука, 1977
8. Ашурлы З.И., Васьковский Ю.М., Гордеева И.А., Малышев Л.В., Ровинский Р.Е.,
Холодилов А.А., Электроразрядный импульсный СО2 лазер,
Квантовая электроника,
т.7, №7, 1980
9. Аполлонов В.В., Васьковский Ю.М., Жаворонков М.И., Прохоров А.М., Ровинский Р.Е.
Мощный электроразрядный СО2 лазер с добавками в смесь легкоионизуемых веществ,
Квантовая электроника, т.12, №1, 1985
© 2001 Reomar Rovinsky