Prefacio
1. Mecánica
2. Propiedades de los Fluidos
3. Gases
4. Fenómenos Térmicos
5. Sonido y Luz
6. Varias
7. Apéndice
73. El problema de la bañera.
a) Una bañera de paredes verticales se llena con agua de grifo en 8 min, y se vacía por medio del orificio de desagüe (el grifo está cerrado) en 12 min. ¿Cuánto tiempo deberá permanecer abierto el grifo para llenar completamente la pila vacía mientras está abierto el desagüe?
 |
b) La pila se llena en 8 min; con el grifo cerrado se tarda el r mismo lapso en vaciarla mediante el orificio de salida. ¿Qué cantidad de agua habrá en ella si durante las veinticuatro horas se vierte agua de grifo mientras el desagüe está abierto?
c) Resuélvase este mismo problema si el tiempo de llenado es 8 min, y el de vaciado, 6 min.
d) Resuélvase idéntico problema, pero llenándose a los 30 min y vaciándose en 5 min.
e) La pila se vacía en un lapso más corto que el de llenado mediante el grifo. ¿Habrá agua en la bañera si empezamos a echar agua dejándola salir al mismo tiempo?
A continuación ofrecemos sendos pares de respuestas a las cinco preguntas planteadas; en una columna se ofrecen las respuestas correctas y en la otra, incorrectas.
| a) La bañera se llenará hasta los bordes en 24 min. | a) La bañera nunca se llenará hasta los bordes. |
| b) La bañera estará vacía. | b) El agua llegará hasta 1/4 de la altura de la pila. |
| c) No habrá agua en la pila. | c) El agua subirá hasta las 9/64 de la altura de la pila. |
| d) No habrá agua en la pila. | d) El agua subirá hasta 1/144 de la altura de la bañera. |
| e) La pila estará vacía. | e) En la bañera habrá un poco de agua. |
¿En qué columna, pues, están las respuestas correctas?
Las de la columna izquierda parecen ser verosímiles. Pero, en realidad, lo son las de la derecha. Por cierto, a primera vista estas respuestas parecen ser muy extrañas; no obstante, vamos a analizar por separado cada uno de estos problemas.
a) En la bañera se vierte más agua que la que sale, sin embargo, en la columna derecha se afirma que nunca se llenará. ¿Por qué? Es que surge la idea de que es muy fácil calcular dentro de cuántos minutos el agua empezará a desbordarse. Cada minuto se llena 1/8 parte del volumen de la pila, mientras que sale 1/12; por consiguiente, el aforo por minuto es
parte de su capacidad. Está claro que en 24 minutos se llenará.
b) En el segundo problema el tiempo de llenado equivale al de vaciado. Por lo tanto, la cantidad de agua que ingresa cada minuto es igual a la que sale. Esto quiere decir que en la pila no deberá quedar ni una sola gota de agua, por más que dure el proceso. Sin embargo, en la columna de respuestas correctas se afirma que el nivel de agua llegará hasta un cuarto de la altura de la bañera.
c), d) y e). Es obvio que en los tres casos sale mayor cantidad de agua que entra, mas, en la segunda columna se asevera que no obstante ello en la pila se acumulará cierta cantidad de líquido.
En suma, las respuestas que damos por correctas, parecen ser absurdas. Para cerciorarse de que realmente son correctas, el lector tendrá que seguir una cadena bastante larga de razonamientos. Empecemos por el primer problema.
a) éste viene a ser una versión del famoso problema del depósito, que se remonta a Herón de Alejandría. Surgido hace más de dos milenios, el problema sigue figurando en muchos libros de problemas de matemáticas escolares, sin que por ello deje de ser errónea, desde el punto de vista de la física, su solución tradicional. Esta última se basa en la suposición equivocada de que el agua sale del recipiente en chorro uniforme mientras su nivel desciende.
Dicha suposición contradice la ley física que afirma que la velocidad de salida del líquido disminuye mientras desciende su nivel. Por consiguiente, es erróneo creer, como suelen hacer los escolares en las clases de matemáticas, que si la pila se vacía en 12 min, cada minuto sale una dozava parte de su contenido inicial. En realidad, el líquido sale de la manera siguiente: inicialmente, mientras su nivel es bastante alto, cada minuto sale más de una dozava parte de la pila llena; esta cantidad va disminuyendo progresivamente por instantes, y cuando su nivel es muy bajo, cada minuto sale menos de una dozava parte del contenido inicial. Por esta razón, el volumen de agua que sale durante este lapso equivale, sólo por término medio, a una dozava parte del de la pila llena, mientras que de hecho el gasto no será exactamente igual a una dozava parte, sino que un poco mayor o menor.
En general, el vaciado de la bañera se asemeja mucho a la marcha del reloj de bolsillo descrita por Mark Twain en tono de broma: el reloj marchaba bien «por término medio», al dar el número correspondiente de vueltas durante las veinticuatro horas. Mas, en la primera mitad de este tiempo adelantaba demasiado retrasándose extremadamente durante el resto de la jornada. Resolver el problema de la pila partiendo de la velocidad media de salida del agua sería lo mismo que consultar el reloj descrito por el famoso escritor estadounidense.
Según vemos, la versión simplificada de este problema, que se resuelve tan fácilmente en la escuela, hay que sustituirla por la variante real ajustándola a las leyes de la naturaleza. Obrando de esa manera obtendremos un resultado distinto. Al comenzar a llenar la bañera mientras el nivel de agua no es alto, sale menos de una dozava parte de su capacidad total; en cambio, cuando el nivel es alto, sale más de una dozava parte. Por ello, el gasto puede ser una octava parte de su volumen, y podrá igualarse con la cantidad de agua que ingresa, antes de que se llene toda la pila. A partir de este instante el nivel dejará de ascender, puesto que el agua afluente saldrá por el desagüe. El nivel se mantendrá constante por debajo de los bordes de la bañera. Claro está que en semejantes condiciones nunca se llenará completamente. Según veremos más adelante, el cálculo matemático confirma lo que acabamos de deducir.
b) En este apartado la corrección de nuestra solución es mucho más evidente. El tiempo de llenado y de vaciado es uno mismo, 8 min. Mientras el nivel es bajo, o sea, cuando se empieza a añadir agua, cada minuto se llena una octava parte de la capacidad de la pila, y sale, según explicamos más arriba, menos de una octava parte. En resumidas cuentas, el nivel deberá elevarse hasta que el caudal afluente se iguale con el gasto. Por consiguiente, en la pila siempre habrá agua. Se puede demostrar -muy pronto lo haremos que siendo iguales el tiempo de llenado y de vaciado, la altura del nivel real deberá equivaler a un cuarto del de la pila llena.
c), d) y e) Después de lo que acabamos de exponer no se requieren muchas aclaraciones para desvanecer las dudas en torno a nuestras respuestas a las tres preguntas restantes. En ellas, el tiempo de vaciado es menor que el de llenado. Es imposible llenar completamente la pila ateniéndose a estas condiciones, mas, se puede asegurar cierta capa de agua, aunque el flujo entrante sea exiguo.
Hay que recordar que las primeras porciones de agua que se añaden, no podrán salir con la misma rapidez, pues mientras el nivel es bajo, la velocidad de salida será muy pequeña; al descender el nivel de líquido, esta magnitud se vuelve cada vez menor que cualquier velocidad constante de llenado. Por ende, en la bañera deberá haber una capa de agua, aunque sea muy pequeña. En otras palabras, contrariamente al «sentido común», en todo tonel -por más rajado que esté- siempre habrá un poco de agua a condición de que se agregue uniforme e ininterrumpidamente la cantidad de agua correspondiente.
Ahora pasemos al examen matemático de los mismos problemas. Nos daremos cuenta de que los ejercicios elementales que se ofrecen a los escolares desde hace dos milenios, requieren conocimientos y hábitos que rebasan el marco de la aritmética elemental.
Para un recipiente de forma cilíndrica (en general, para uno de paredes verticales) vamos a establecer cierta dependencia entre el tiempo T de llenado, ídem t de vaciado y la altura l del nivel constante de líquido si el llenado se efectúa con el orificio de desagüe destapado. Para ello convengamos en utilizar las designaciones siguientes:
H, la altura del nivel de líquido en el recipiente lleno;
T, el tiempo de llenado hasta el nivel H;
t, ídem de vaciado del recipiente a partir del nivel inicial H;
S, la sección del recipiente;
c, ídem del desagüe;
w, la velocidad de descenso del nivel en el recipiente por segundo;
v, ídem de salida del líquido por segundo;
l, la altura del nivel constante mientras el orificio de vaciado está destapado. Está claro que si en un segundo el nivel desciende en w, en el mismo lapso por el desagüe deberá salir una cantidad Sw de líquido, equivalente al volumen de la columna cv del chorro que sale:
de donde
No obstante, la velocidad v de salida del líquido se determina por la fórmula de Torricelli citada más arriba,
, donde l es la altura del nivel y g, la aceleración de la gravedad. Por otro lado, la velocidad w de ascenso del nivel de líquido cuando el orificio está tapado, es H/T. El nivel será constante cuando la velocidad de su descenso sea igual a la de ascenso, es decir, si tiene lugar la igualdad siguiente:
Haciendo uso de esta fórmula hallamos la altura l del nivel estabilizado [1]
ésta es la altura del nivel de líquido contenido en el recipiente durante el ingreso de agua mientras el desagüe está destapado.
Simplificamos esta fórmula eliminando las variables S, c y g. El descenso del nivel de líquido en el recipiente de paredes verticales (mientras el grifo permanece cerrado) es un movimiento uniformemente variable que comienza con la velocidad w y termina con la velocidad nula. La aceleración a de semejante movimiento se determina a partir de la ecuación siguiente:
de donde:
Si ponemos el valor de w de la expresión w = cv/S y tenemos en cuenta que
obtenemos el resultado siguiente:
Además, para el caso del movimiento que estamos analizando
de donde
Realizando la sustitución en la fórmula [1], obtendremos el resultado siguiente:
Así pues, para las condiciones enunciadas, el nivel de líquido contenido en el recipiente deberá mantenerse a una altura equivalente a la del recipiente lleno y se determinará mediante la fórmula que sigue:
Ahora vamos a utilizar la fórmula deducida para resolver nuestros problemas.
a) La duración de llenado es T = 8 min y el tiempo de vaciado t = 12 min. La altura l del nivel límite referida a la del recipiente H, equivale a
partesEl nivel de agua sólo alcanzará 9/16 partes de la altura de la bañera. Por más que se añada agua, su nivel no se elevará después.
b) En este caso T = t = 8 min:
El nivel ascenderá a un cuarto de la altura del recipiente.
c) Para T = 8 min y t = 6 min:
El agua alcanzará 9/64 partes de la altura de la pila.
d) T= 30 min y t = 5 min:
El nivel de líquido equivaldrá a 1/144 parte de la altura de la bañera.
e) t < T:
La expresión obtenida podrá ser igual a cero siempre que se observen las dos condiciones que siguen:
1) t = 0 y T ¹ 0. Esto quiere decir que la bañera se vacía instantáneamente, lo cual es imposible.
2) t ¹ 0 y T = ¥ . Es decir, con el desagüe tapado el tiempo de llenado será indefinido. En otras palabras, la afluencia de agua por segundo es nula, no ingresa líquido en la bañera. En la práctica este caso equivale a que la llave esté cerrada.
Así pues, siempre que el grifo esté abierto y la pila no se vacíe instantáneamente, l nunca podrá ser nula: la capa de agua siempre tendrá altura finita.
¿Bajo qué condiciones, pues, sería posible llenar toda la pila con el orificio abierto? Evidentemente, cuando l = H, es decir, cuando
Por tanto, si el tiempo de llenado es dos veces menor que el de vaciado, será posible llenarla por completo, aunque el orificio esté abierto.
También sería interesante calcular cuánto tiempo se necesitará para alcanzar un nivel constante. Este problema no se resuelve por medio de las matemáticas elementales; habrá que valerse del cálculo integral. Ofrecemos el cálculo correspondiente a los que se interesan por esta variante; aquellos lectores que tienen conocimientos de matemáticas superiores podrán omitir el análisis que se expone a continuación, y sólo emplear la fórmula deducida al final del cálculo.
La velocidad de elevación del nivel de líquido en un recipiente al que se añade agua mientras el orificio de desagüe está destapado, se define como la diferencia entre la velocidad de ascenso del nivel con el orificio tapado (H/T) y la de descenso del mismo sin agregar líquido, (Nota:
, donde x es la altura del nivel de agua en un instante dado). Por consiguiente, la velocidad de ascenso del nivel en el momento dado será
de donde
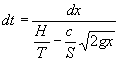
El tiempo necesario para que el nivel de líquido suba hasta la altura x = h se designa por Q .
Integrando la ecuación
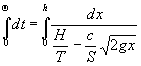
obtenemos la siguiente fórmula para determinar el tiempo Q que se necesita para que el nivel de líquido alcance la altura h:
(aquí, ln denota el logaritmo de base e = 2,718...).
Esta expresión puede ser simplificada. Partiendo de las igualdades wS = vc y
, se determina la velocidad w de descenso del nivel desde la altura h al vaciar la pila:
Por consiguiente,
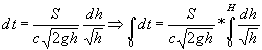
de donde
Después de realizar las sustituciones correspondientes se obtiene la siguiente expresión para determinar Q :
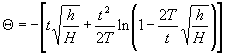
la cual no contempla los casos de sección S y c del recipiente y del orificio de salida ni la aceleración de la gravedad g. Esto último señala que el tiempo de llenado de la bañera debe ser el mismo que en cualquier otro planeta.
Si deseamos averiguar cuánto tiempo se necesitará para alcanzar los niveles límites en los recipientes, llegaremos a la conclusión de que esta magnitud será indefinida, o sea, nunca se llenarán. Esta respuesta es bastante inesperada: se podría preverla, pues a medida que el nivel se aproxima a la altura límite, disminuye progresivamente su velocidad de elevación; cuanto más cerca esté el nivel de líquido a su límite, tanto menos tenderá a él. Queda claro que el agua nunca lo alcanzará, por mucho que se le acerque.
No obstante, desde el punto de vista práctico, es posible formular el problema de un modo distinto. Pues, en este caso no es obligatorio que el nivel de agua coincida exactamente con el límite; por ejemplo, pueden diferir en 0,01 de altura. El tiempo que se necesita para que el agua alcance este nivel «aproximado» se determina mediante la fórmula deducida poniendo h = 0,991, donde l es la altura del nivel límite; de modo que resulta que
Apliquemos la fórmula
a los casos que examinamos con anterioridad.
a) T = 8min y t = 12 min:
minEl nivel constante se alcanzará en unos 39 min.
b) T = t = 8 min:
minEl líquido alcanzará el nivel constante en unos 17 min
c) T = 8 min y t = 6 min:
minEl nivel de líquido será constante dentro de unos 10 min.
d) T = 30 min y t = 5 min:
minDe hecho, el líquido alcanzará el nivel límite en menos de dos minutos.
e) Finalmente, la pila con el desagüe abierto se llenará totalmente, lo que ocurre -según determináramos anteriormente- a condición de que t = 2T, en un tiempo
Con esto damos por terminado el análisis de los problemas de la bañera, que se nos ha hecho tan largo. Es que el asunto es mucho más complicado de lo que se imaginan aquellos autores de libros de problemas de matemáticas que a la ligera incluyen en sus obras «problemas de los depósitos», destinados a los alumnos de la escuela primaria.
|
|
|