Prefacio
1. Mecánica
2. Propiedades de los Fluidos
3. Gases
4. Fenómenos Térmicos
5. Sonido y Luz
6. Varias
7. Apéndice

238. La mecánica escolar y la teoría de la relatividad.
¿Cómo deberíamos enfocar la mecánica escolar desde el punto de vista de la teoría de la relatividad? ¿Tiene aún validez?
Desde que en la ciencia se estableció el llamado principio de relatividad de Einstein, las leyes fundamentales de la mecánica tradicional ya no parecen tan firmes como antes, aunque generalmente se creía que se mantendrían inalterables eternamente. Entre los no especialistas que oyeron algo de esta revolución ocurrida en la ciencia, se arraigó la opinión de que los principios de la mecánica creada por Galileo y Newton, sobre los cuales se asientan la técnica y la industria, se han vuelto obsoletos y deben ir a parar al archivo de la ciencia.
Hubo una época en que el hecho de que las tesis de la mecánica clásica seguían figurando en los libros de texto y en las publicaciones sobre temas técnicos, dejaba perplejas a las personas no muy enteradas de cómo es el estado de cosas en ese terreno. Incluso a veces se llegaba a calificar de retrógrados a los autores de artículos y libros técnicos que se atenían en sus cálculos a la «ley metafísica de independencia de la acción de las fuerzas», establecida por Galileo, a la ley de invariabilidad de la masa, formulada por Newton, etc.
Para esclarecer el asunto, vamos a analizar una de las leyes fundamentales de la mecánica clásica a saber, la de adición de velocidades. Conforme a esta ley, la regla de adición de las velocidades v y v1 cuyos sentidos coinciden, tiene la siguiente forma matemática:
La teoría de la relatividad rechazó esta ley simple y la sustituyó por otra, más compleja, con arreglo a la cual la velocidad u siempre es menor que v + v1 . La ley clásica resultó ser errónea. Pero ¿hasta qué punto? ¿Sufriremos algún daño si seguimos aplicando la regla antigua? Vamos a examinar la nueva fórmula de adición de velocidades. Hela aquí:
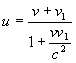
En esta expresión, las letras u, v y v1 denotan lo mismo que antes, mientras que c designa la velocidad de la luz. Esta nueva fórmula sólo difiere de la antigua en el término vv1 /c2, el cual suele tener valores muy pequeños si las velocidades v y v1 no son muy elevadas, puesto que la velocidad de la luz c es extremadamente alta. Lo explica el siguiente ejemplo concreto.
Hagamos un cálculo para velocidades no muy grandes, típicas para la técnica moderna. La máquina más rápida es la turbina de vapor. Al dar 30.000 revoluciones por minuto y tener 15 cm de diámetro, su rotor desarrolla una velocidad lineal de 225 m/s. Los obuses tienen una velocidad más elevada, de 1 km/s. Adoptemos v = v1 = 1 km/s y sustituyámosla en ambas fórmulas, antigua y nueva; c es la velocidad de la luz, igual a 300.000 km/s.
Según la fórmula clásica u = v + v1 , u = 2 km/s. La fórmula nueva adopta la forma

y proporciona el resultado siguiente:
Por supuesto, hay cierta diferencia, pero ¡tan sólo equivalente a una milésima del diámetro del átomo más pequeño!
Recordemos que las mediciones más exactas de la longitud no sobrepasan la séptima cifra del resultado, en tanto que en la técnica se suele conformar con la cuarta o la quinta cifras; en nuestro caso los resultados obtenidos sólo difieren en la décimosegunda cifra, de modo que la diferencia vale 0,000 000 000 002.
El resultado casi no cambia si la velocidad es más alta aún; por ejemplo, en el caso de las naves propulsadas por cohetes cuya velocidad supera decenas de veces la del obús.
Por tanto, para la técnica la ley «clásica» de adición de velocidades no se ha vuelto «metafísica»: ésta sigue controlando todos los movimientos. Y sólo si las velocidades son mil veces superiores a la del cohete interplanetario (es decir, de decenas de miles de kilómetros por segundo) empieza a sentirse la inexactitud de la regla antigua de adición de velocidades. No obstante, por el momento la técnica no tiene que enfrentarse con semejantes velocidades que se examinan en la física teórica y en la experimentación en el laboratorio, en cuyo caso se utiliza la fórmula nueva.
Ahora abordemos la ley de constancia de la masa. La mecánica newtoniana está basada en la tesis de que la masa es inherente a un cuerpo dado, independientemente del estado en que éste se encuentra. La einsteiniana, en cambio, afirma lo contrario: la masa de un cuerpo no es constante, sino que aumenta cuando dicho cuerpo está en movimiento. Si esto es así, ¿serán erróneos todos los cálculos técnicos convencionales?
Examinando el ejemplo de un obús disparado, vamos a ver si podemos o no determinar la diferencia esperada. ¿En qué cantidad aumentará la masa del obús durante el movimiento? La teoría de la relatividad sostiene que el aumento de masa del cuerpo en movimiento, cuya masa en estado de reposo era m, es igual a

donde v es la velocidad del cuerpo y c, la de la luz.
Si usted efectúa el cálculo para v = 1 km/s, hallará que el incremento de masa de un proyectil disparado equivale a 0,000 000 000 005 de su masa en estado de reposo.
Según vemos, la masa ha aumentado en una magnitud imposible de determinar mediante el pesaje más exacto. La balanza más exacta permite determinar la masa con una exactitud de hasta 0,00000001 de su valor. Por cierto, semejante utensilio sería incapaz de registrar una diferencia mil veces mayor que la que generalmente es despreciada por la mecánica vieja. En el futuro, durante los vuelos de las naves interplanetarias que se desplazarán con velocidades de una decena de kilómetros por segundo, la masa de todos los objetos dispuestos en ellas aumentará en 0,0000000005 del valor de su masa en reposo. Esta magnitud es mayor, pero tampoco será posible medirla.
Por consiguiente, en lo que se refiere a la ley de constancia de la masa, hemos de repetir lo que explicamos respecto de la ley de adición de velocidades: prácticamente, esta ley sigue en vigor, de modo que los ingenieros pueden aplicarla sin temor a cometer un error notable. Es distinto el caso de los físicos que efectúan cálculos o experimentos con electrones rápidos (su velocidad puede ser del 95% de la de la luz y aún más); éstos tienen que atenerse a las leyes de la nueva mecánica.
Y ¿qué pasa constancia de la masa, o sea, con el gran principio de Lavoisier, en la química? Estrictamente hablando, en la actualidad habría que darlo por inexacto. Según Lavoisier, cuando se combinan químicamente 2 g de hidrógeno y 16 g de oxígeno, deberán proporcionar exactamente 18 g de agua. Pero según Einstein, en vez de 18 g se obtendrá menos, a saber,
Esta diferencia sólo se advierte sobre el papel; es imposible detectarla mediante una balanza.
Así pues, podemos afirmar, sin restricción alguna, que las tesis de la mecánica de Einstein no cambian nada en la técnica moderna. La industria puede seguir contando con el apoyo seguro de las leyes de la mecánica newtoniana.
|
|
|
|