
I spent two years at college studying Mathematics and Further Mathematics A-Levels and then three years at the University of Sheffield obtaining a first class honours degree. I left University in 1994 but I still enjoy the subject.
This page will be updated frequently and will contain lots of interesting facts and figures along with some intriguing Mathematical formulas and proofs. Starting with:

The Newton-Raphson method (sometimes just called the Newton method) is one of the most widely used methods of solving non-linear algebraic equations of the form f(x) = 0
It basically works by extrapolating along the tangent (more of that later) but in layman's terms you start by guessing at a solution, feed that guess through Newton's method and it returns a better guess. Then you simply feed the better guess through the method to get an even better one. These guesses eventually converge to a solution (with a few exceptions). The interesting thing about this method is that, because most functions have more than one solution, different initial guesses that are close together can lead to wildly different solutions. Anyone who is interested in Chaos Theory may already be thinking about SDIC (Sensitive Dependence on Initial Conditions) and indeed some very interesting fractal structures can be drawn using this method (again, more later).
So onto the mathematics behind the method.
We have a non-linear algebraic function f(x) and we are interested in the solutions to f(x) = 0. The first thing to do is choose our initial guess, lets call this x0. We also need to look at f(x0) and f '(x0) [Using the shorthand f '(x) to indicate the derivative of f(x) with respect to x.]
Looking at the tangent to the curve at f(x0) we find that tan(q) = f '(x0), and so f '(x0) = f(x0) / (x0 - x1),
Therefore x1 = x0 - f(x0)/f '(x0)
or in general xn+1 = xn - f(xn)/f '(xn)
If an initial x0 is chosen which leads to a f '(xn) which is close to zero then convergence to a root cannot be guaranteed but in general the Newton method converges more rapidly than other similar methods (such as the method of bisection). Also note that the formulation breaks down at a multiple root as f '(x) = 0 at such points.
As I mentioned earlier some interesting structures can be drawn such as the one below

The above is an Argand diagram showing convergence to the four roots of x4 - 1 = 0. [the roots being 1, -1, i, -i]
Each point plotted is coloured depending on which root the point converges to using Newton's method and as you can see the boundaries become very complex and display self-similarity when zoomed into. The picture was created using a program that I wrote using Borland's Delphi 2 programming language. I first read about the chaotic nature of the equation in the book Chaos by James Gleick [ISBN: 0 7474 0413 5]. The program I created was basically for fun and to look at other equations of the same family (and really to prove to myself that I could). I have included it on this site for download if you are interested, I cannot promise that it will be of any use because I created it for myself and so the functionality and user-friendliness probably isn't too good but I'm sure I could make it better if I found the time and inclination.
Download Newton_Raphson_1_01.zip (116kb) version 1.01 by S. Kennedy

Consider an equilateral triangle with a surface area of one square unit.

Now remove an inverted equilateral triangle from the centre of the original triangle as shown below:

This can now be thought of as three separate triangles. Each of which has a surface area a quarter of that of the original triangle. So the total surface area of the triangles is (3 * 1/4) = 3/4. Repeat the process for each of these three triangles.

This produces 9 triangles (3x3) each of which have one sixteenth the surface area of the original triangle. Therefore the total surface area of the above set of triangles is 9 * 1/16 = 9/16 [Aside: = (3x3)/(4x4)]. Repeat the process again.

We now have 27 triangles (3x3x3) each of which has a surface area that is one sixty-fourth of the original. The total surface area then becomes 27 * 1/64 = 27/64 [(3x3x3)/(4*4*4)].
A pattern starts to emerge here. We see that after the nth stage we end up with 3n triangles with a total surface area of 3n/4n. If we continue to do this we see that at the limit as n approaches infinity the number of triangles approaches infinity but the total surface area of these triangles approaches zero. The Sierpinski Gasket is this limit set. It can actually be constructed in several ways another is shown below.






In the above series each square has the bottom right quadrant removed (or the top left, top right and bottom left quadrants are replaced with a scaled copy of the full picture). As the process is repeated the same pattern emerges.
Now consider the following simple rules:
1. Mark three points on a piece of paper that form an equilateral triangle. Label these A, B and C
2. Draw a blue dot at A.
3. Randomly choose one of the three lettered points and draw a dot halfway between the dot you just drew and the point chosen. Colour this dot blue if the randomly chosen point was A, green if the point chosen was B and red if it was C.
4. Repeat step three as many times as you like.
Now what do we end up with? A random collection of coloured dots? The outline of a triangle? A multi-coloured speckled solid triangle? Well lets take a look. (The number of dots plotted is 500, 2000, 5000, 25000, 50000 and 100000 respectively.)





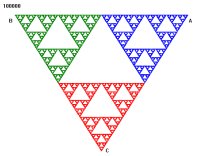
By following the above rules every dot that is drawn on the page will fall into the set for the Sierpinski Gasket. In other words instead of ending up with a random collection of dots as might be expected you will find that a picture will emerge (when enough dots have been plotted) just like the above pictures. (Click on the pictures for a larger version).
The above pictures were created using a fairly simple Delphi v2 program. To take a look at the source code for this program click here: Sierpinski Gasket Code. To download the program (which also includes a Sierpinski Carpet generator) click here: Downloads

Consider the following: k * 2n + 1 for some integers k and n. Obviously the result of this would always be an odd number but under what conditions would it be prime?
The table below gives some results for small values of k and n.
| n = 1 | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 | n = 7 | n = 8 | |
| k = 3 | 7 | 13 | 25 | 49 | 97 | 193 | 385 | 769 |
| k = 4 | 9 | 17 | 33 | 65 | 129 | 257 | 513 | 1025 |
| k = 5 | 11 | 21 | 41 | 81 | 161 | 321 | 641 | 1281 |
| k = 6 | 13 | 25 | 49 | 97 | 193 | 385 | 769 | 1537 |
| k = 7 | 15 | 29 | 57 | 113 | 225 | 449 | 897 | 1793 |
| k = 8 | 17 | 33 | 65 | 129 | 257 | 513 | 1025 | 2049 |
I have highlighted in red all results that are prime numbers. For these 48 results 17 of the k and n combinations produce prime numbers. Several questions arise from this: as n and k get bigger are primes still produced? given some set of k and n is it possible to work out exactly how many primes will be produced? do certain values of k never produce a prime for any n? and many more.
Lets take a look at that last question "do certain values of k never produce a prime for any n?".
Is it possible to find an integer k so that k * 2n + 1 will never be a prime number for any integer n? Perhaps surprisingly the answer is yes. These values of k are called Sierpinksi Numbers due to the fact that the Polish mathematician Waclaw Sierpinski not only showed that they existed but, even more surprisingly, proved that there were an infinite amount of them. One of the mathematics world great unsolved problems is trying to determine the smallest Sierpinski Number. One candidate has been known since 1962 when John Selfridge discovered that k = 78557 is a Sierpinski Number. But are there any smaller than that?
At the beginning of 2002 only 17 numbers less that 78557 were still in doubt (every other integer less than 78557 had been shown to produce a prime number for at least one value of n). It was then that Louis Helm and David Norris began a distributed computing program that would check each of these 17 numbers to see if they really were Sierpinski Numbers. Their project called Seventeen or Bust (www.seventeenorbust.com) has, in its first year, proved that 5 of the values produce prime numbers and so are not Sierpinski Numbers. The project has approximately 1800 computer users around the world testing the remaining 12 numbers and if you would like to lend a hand please visit their site and sign up.