SIMULACIÓN DE MOVIMIENTO DE CUERPOS

Modelos Dinámicos

Beatriz Loubet

modelos de movimiento de cuerpos

Se define la velocidad instantánea de un cuerpo como:

, donde de es el cambio de posición, y dt es un intervalo infinitesimal de tiempo.

La posición de un cuerpo en el espacio está definida por 3 coordenadas: x, y, z.

La posición de un cuerpo en el plano está definida por 2 coordenadas: x, y. Nos limitaremos a movimiento en dos dimensiones.

La velocidad se puede entonces descomponer en dos componentes: v_x y v_y, la velocidad en la dirección horizontal y la velocidad en la dirección vertical.

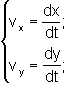
Despejando:

Discretizando: (convirtiendo las ecuaciones diferenciales en ecuaciones en diferencia):

Como D x = x_t - x_{t -1}, y D y = y_t - y_{t -1}:

Estas ecuaciones en diferencia nos servirán para simular el movimiento de cualquier cuerpo.

Si un cuerpo tiene movimiento acelerado, es decir, su velocidad cambia, recordemos que se define la aceleración como el cambio de velocidad en la unidad de tiempo:

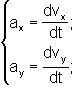
de donde, siguiendo un procedimiento análogo al anterior:

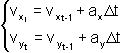
Estas ecuaciones nos permiten actualizar la velocidad en cada iteración.

Esquema de la simulación del movimiento

• Establecemos valores iniciales de x, y, v_x, v_y, Dt.
• Repetimos el siguiente procedimiento hasta finalizar:
• Recalculamos v_x, v_y si es necesario.
• Recalculamos x e y.
• Graficamos (para la trayectoria del móvil, con una línea que una la posición anterior con la actual; para la posición del móvil, borramos el móvil de la posición anterior, y lo graficamos en la posición actual).
• Hacemos una pausa, para que pueda verse el movimiento.

La pantalla y las coordenadas

Una pantalla es un rectángulo de m x n píxeles:

Observemos que el eje X coincide con el eje de abcisas de las coordenadas cartesianas, pero el eje Y tiene sentido contrario. Esto lo debemos tener muy en cuenta, pues si el móvil se mueve hacia arriba, disminuye su posición Y, en lugar de aumentar, por lo que su velocidad es negativa.

Las coordenadas son números enteros entre (0,0) y (MaxX,MaxY). Por lo tanto, al actualizar la posición del móvil, debemos redonderar los valores de x , y. Es conveniente, además, para que nuestro móvil pueda verse en cualquier monitor, manejar posiciones relativas y no absolutas.

Modelo Caída Libre

Nota: Este modelo lo deberán presentar todos los grupos.

Este modelo pretende simular el comportamiento de una pelota que es arrojada con una velocidad horizontal, y cae (adquiere velocidad vertical) por acción de la gravedad.

La pelota parte del borde izquierdo de la pantalla, a una altura del 90% de la altura de la pantalla, con una velocidad horizontal v_x = cte, que mantiene a lo largo de la simulación. La velocidad vertical en el inicio es cero, pero tiene una aceleración vertical g = 9.8 m/seg².

Sin embargo, apenas parte la pelota, comienza a sufrir los efectos de la aceleración de la gravedad, con lo que:

Por lo que antes de actualizar la posición de la pelota, habrá que recalcular la velocidad vertical.

Al caer al suelo, (borde inferior de la pantalla), la pelota debe rebotar, lo que conseguimos haciendo que velocidad vertical cambie de signo. Además, dado que se pierde energía en el rebote, su valor absoluto será menor: digamos el 80% de su valor anterior.

Efectos especiales: sonido al caer al suelo.