Virtual Shadows
Copyright © 1999 Leonardo Boselli. All Rights Reserved.

Task

We want to create the shadow of an object lighted by the sun on a generic plane. The shadow must follow the movements and morphings of the object, of the projective plane and of the light source.

Comments

To reduce the task, we consider an object realized with an IndexedFaceSet. The sun, a very distant linght source , may be represented with a DirectionalLight.

We want an easy movable object, so we must insert it in a Transform node.

The projective plane as usual may be selected giving the origin and the normal vector.

Implementation

We are going to realize this task using the EAI interface, adding the power of the Java language to the presentation capabilities of VRML plug-ins. Finally, we want to build a code compatible with CosmoPlayer 1.0 and WorldView 2.0, included in class 4 browsers and thus viewable by the most part of Internet users, and with CosmoPlayer 2.1, owned by the people passionately fond of VRML. This is an effort we must reach, but it's not simple and sometimes impossible.

Optimizations

As we'll see, our task is too generic to get good results on slow machines.

As a first improvement we can consider the projective plane: a ground at zero height has origin (0,0,0) and normal vector (0,1,0).

Secondly, we have already adopted a light source that is a DirectionalLight instead of a PointLight. This choice saves computational time for every vertex of the object, but we can easily modify the code to support the worst case.

The most important optimization is to renounce to the Transform node that incapsulates the IndexedFaceSet. This convenience brings to heavy coding and takes away a lot of CPU time.

Last consideration about performances: Java is fast enough when there are conputations in cycles, thanks to JIT (Just in Time Compilers). We choose to use several classes to improve readability, but the execution speed will be reduced, due to the use of many virtual methods.

Formulae

To draw the shadow we must project every vertex on the plane. We get a flat copy of the object, that we'll paint in a transparent shade of black. Using the 3-dimensional vector geometry, we have

• P': vector projected on the plane
• P: vertex of the object
• O: origin of the plane
• N: normal of the plane
• D: direction of a ray of light (with a PointLight we must substitute to D the normalized difference P - L, where L is the position vector of the source).

If the plane is the ground at zero height, the formula simply becomes

It's a harder problem to modify the coordinates of the vertex following the Transform node. The Transform changes the coordinates of a point P with a matrix like this

(T translation, R rotation, S scale, SR rotation before scale, C translation of the rotation center - more details in VRML 2.0 Specifications). The calculations are complex and we consider only T, C e R avoiding S and SR. We can simulate scale operations with a change in the vertex locations. Finally our transform is

We consider the following relations (translation coordinates are T_X, T_Y, T_Z and the object rotates of an angle a around the vector D_X, D_Y, D_Z) :

The Shadow

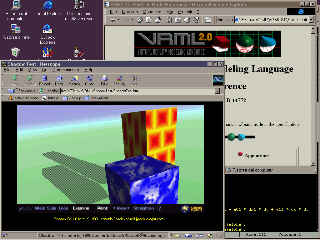
To build the shadow we need to get the coordinate of the vertexes (exposedField coord in IndexedFaceSet) and the indexes that made up the faces (field coordIndex). CoordIndex is a field and we can't get it from existing objects. However we create the object with Java and we can access the vector of the indexes.

Example

In the picture we show the running of the program. There are two objects lightened by our virtual sun. One of them rotates and the other morphs. To view the world with a VRML plug-in click on the picture on the left.

Finally... the Code

In the writing of the code we have used a lot of classes that incapsulate the VRML nodes. The complete set of classes can be found in VirtualShadows.zip.
It's available the documentation generated by javadoc to made the class hierarchy more comprehensible.
In the following page you can find the parts of the code that build the shadow and the methods used by the Shadow class.
Good reading!