Virtual Shadows
Copyright © 1999 Leonardo Boselli. All Rights Reserved.

Obiettivo

Vogliamo creare l'ombra di un oggetto illuminato dal sole su un piano generico. L'ombra deve seguire le trasformazioni e deformazioni dell'oggetto, del piano di proiezione e della sorgente luminosa.

Commenti

Per restringere il campo della nostra indagine, consideriamo un oggetto generico realizzato per mezzo di un IndexedFaceSet. Il sole, nella sua qualità di sorgente luminosa molto lontana , può essere rappresentata con una DirectionalLight.

Se vogliamo che l'oggetto da illuminare sia facilmente gestibile, dobbiamo prevedere di inserirlo in un nodo Transform.

Per quanto riguarda il piano di proiezione, possiamo individuarlo fornendo l'origine ed il vettore normale, come si usa di solito in geometria.

Implementazione

Prevediamo di realizzare questo obiettivo utilizzando l'EAI in modo da sfruttare le potenzialità elaborative del linguaggio Java e le capacità di visualizzazione dei plug-in VRML. Come ultima richiesta vogliamo che il codice sia compatibile con CosmoPlayer 1.0 e WorldView 2.0, di serie sui browser di classe 4 e quindi fruibili dalla maggior parte degli utenti di Internet, e con CosmoPlayer 2.1, ultimo nato dei plug-in, ma diffuso solo tra gli appassionati del VRML. Questo è uno sforzo che, con la situazione attuale, deve essere fatto, ma che non sempre e' possibile ottenere.

Ottimizzazioni

I nostri obiettivi, come vedremo, sono troppo generici per ottenere buoni risultati su macchine lente.

Una prima ottimizzazione riguarda il piano di proiezione: nel caso del terreno a quota zero avremo semplicemente origine (0,0,0) e normale (0,1,0).

Una seconda ottimizzazione è già stata adottata considerando una DirectionalLight invece di una PointLight. Questa fa risparmiare diversi calcoli per ogni vertice dell'oggetto, ma può comunque essere facilmente modificata.

La più importante ottimizzazione consiste nel rinunciare al nodo Transform che incapsula l'IndexedFaceSet. Questa comodità, infatti, porta calcoli notevolmente più complicati.

Ultima considerazione per quanto riguarda le performance: Java è un linguaggio sufficientemente veloce quando ci sono molti calcoli racchiusi in cicli, grazie ai JIT (Just in Time Compilers), e da questo punto di vista IE4 batte la concorrenza (almeno per ora - fine 1998). Noi, però, utilizzeremo diverse classi per migliorare la leggibilità del codice e quindi, a causa delle chiamate a numerosi metodi virtuali, perderemo in velocità di esecuzione.

Formule

Per disegnare l'ombra dobbiamo proiettare ogni vertice dell'oggetto sul piano. Si ottiene una copia dell'oggetto schiacciata, che coloreremo di nero e renderemo semitrasparente. Usando l'usuale geometria vettoriale nello spazio, si ricava

• P': vettore proiettato sul piano
• P: vertice dell'oggetto
• O: origine del piano
• N: normale del piano
• D: direzione della luce (nel caso di una PointLight dobbiamo sostituire a D la differenza P - L normalizzata, dove L è il vettore posizione della sorgente).

Se il piano è il terreno a quota zero, la formula diventa semplicemente

E' un problema molto più complesso trasformare le coordinate dei vertici seguendo il nodo Transform. Com'è noto, il Transform modifica le coordinate del punto P secondo questa matrice

(T traslazione, R rotazione, S trasformazione di scala, SR rotazione prima della scalatura, C traslazione del centro di rotazione - per maggiori informazioni vedi le specifiche del VRML 2.0). Data la complessità dei calcoli terremo conto solo delle matrici T, C e R evitando di considerare le trasformazioni di scala, che saranno eventualmente simulate intervenendo sulla posizione dei vertici. In conclusione la nostra trasformazione è

La forma delle matrici che verranno utilizzate nel codice è la seguente (Le coordinate della traslazione sono T_X, T_Y, T_Z, mentre la rotazione è di un angolo a attorno al vettore D_X, D_Y, D_Z) :

L'ombra

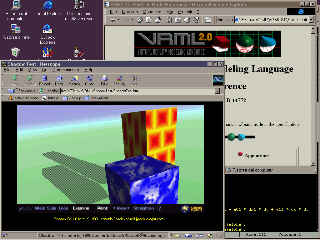
Per creare l'ombra bisogna accedere alle coordinate dei vertici (exposedField coord in IndexedFaceSet) e agli indici che determinano le facce (field coordIndex). Poiché coordIndex è un field, non possiamo ottenerlo per oggetti esistenti generici. Nel nostro caso creiamo l'oggetto mediante Java e quindi abbiamo a disposizione il vettore degli indici.

Esempio

Come dimostrazione del funzionamento delle formule ecco due oggetti illuminati dal nostro sole virtuale. Uno dei due ruota, mentre l'altro si deforma. Per visualizzare l'esempio con un plug-in VRML è sufficiente un click sull'immagine a sinistra.

Infine... Il programma

Nella realizzazione del codice sono state usate molte classi che incapsulano i nodi VRML. L'insieme completo delle classi si trova in VirtualShadows.zip.
E' inoltre disponibile la documentazione generata da javadoc per orientarsi nel listato.
Nella pagina seguente è possibile trovare le parti del codice che costruiscono l'ombra ed i metodi utilizzati dalla classe Shadow.
Buona lettura!