

Next: S
Up: R
Previous: Right Inverse
Ring
A ring is a triple 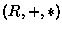 in which + and
in which + and  are Binary Operations on the
Set R , such that (R,+) is an
Abelian Group and
are Binary Operations on the
Set R , such that (R,+) is an
Abelian Group and  is a Monoid. Often authors do not require
a multiplicative Identity. They would call
what we have defined a ring with Unity.
is a Monoid. Often authors do not require
a multiplicative Identity. They would call
what we have defined a ring with Unity.
1999-03-08