This topic is divided into two chapters:
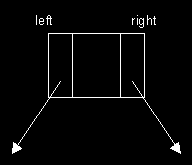
- dynamic data structure that consists of 3 components:
data - to store one data element
left - to point to left node
right - to point to right node
One Binary Tree Node

There are two types of binary trees:
Binary Trees Basics (Part I)
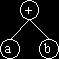
| infix: a + b | infix: b+a |
 |
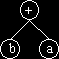 |
| Note: (a + b) is not the same as (b + a) |
| infix: a+b+c | Infix: a + (b+c) |
 |
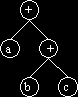 |
[Note : this tree is the same as (a+b)+ c]
a+b is evaluated first because of the left
to right associativity rule (same level-evaluate from left to
right)
| infix: a+b*c | infix: a*b+c |
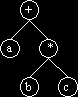 |
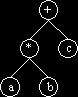 |
| same as a+(b*c) | same as (a*b) +c |
There are three methods of binary tree traversal:
Program BinaryTree1;
Uses Crt;
{ building the binary tree the hard way }
TYPE
TreePtr = ^TreeNode;
TreeNode = RECORD
Data : Char;
Left,
Right : TreePtr;
END;
VAR
Root : TreePtr;
Procedure NewLeaf(var NewElemPtr : TReePtr; Item :Char);
BEGIN
New(NewElemPtr);
NewElemPtr^.Data := Item;
NewElemPtr^.Left := NIL;
NewElemPtr^.Right := NIL;
END;
Procedure BuildTree( VAR Root : TreePtr);
BEGIN
NewLeaf(Root,'9');
NewLeaf(Root^.Left,'7');
NewLeaf(Root^.Right,'2');
NewLeaf(Root^.Right^.Left,'3');
NewLeaf(Root^.Right^.RIght,'5');
NewLeaf(Root^.Right^.RIght^.Right,'1');
END;
Procedure PreOrder(aNode : TreePtr);
BEGIN
IF aNode <> NIL THEN
begin
Write(aNode^.Data : 3);
PreOrder(aNode^.Left);
PreOrder(aNode^.Right);
end;
END;
Procedure InOrder(aNode : TreePtr);
BEGIN
IF aNode <> NIL THEN
begin
InOrder(aNode^.Left);
Write(aNode^.Data : 3);
InOrder(aNode^.Right);
end;
END;
Procedure PostOrder(aNode : TreePtr);
BEGIN
IF aNode <> NIL THEN
begin
PostOrder(aNode^.Left);
PostOrder(aNode^.Right);
Write(aNode^.Data : 3);
end;
END;
Procedure Destroy(R : TreePtr);
BEGIN
IF R <> NIL THEN
begin
Destroy(R^.Left);
Destroy(R^.Right);
Dispose(R);
end;
END;
BEGIN { main program }
ClrScr;
BuildTree(Root);
Write('Preoder :');
Preorder(Root);
WriteLn; WriteLn;
Write('Postorder :');
Postorder(Root);
WriteLn; WriteLn;
Write('Inorder :');
Inorder(Root);
WriteLn; WriteLn;
END.
Sample program 2:
Easier method of creating a binary tree
Program BinaryTree2;
Uses Crt;
{ an
easier way of building the binary tree }
TYPE
DataType = Char;
TreePtr = ^TreeNode;
TreeNode = RECORD
Data : Char;
Left,
Right : TreePtr;
END;
VAR
Root : TreePtr;
Ch : char;
PROCEDURE NewLeaf(var NewElemPtr : TreePtr; Item :Char);
BEGIN
New(NewElemPtr);
NewElemPtr^.Data := Item;
NewElemPtr^.Left := NIL;
NewElemPtr^.Right := NIL;
END;
PROCEDURE PreOrder(aNode : TreePtr);
BEGIN
IF aNode <> NIL THEN
begin
Write(aNode^.Data : 3);
PreOrder(aNode^.Left);
PreOrder(aNode^.Right);
end;
END;
PROCEDURE InOrder(aNode : TreePtr);
BEGIN
IF aNode <> NIL THEN
begin
InOrder(aNode^.Left);
Write(aNode^.Data : 3);
InOrder(aNode^.Right);
end;
END;
PROCEDURE PostOrder(aNode : TreePtr);
BEGIN
IF aNode <> NIL THEN
begin
PostOrder(aNode^.Left);
PostOrder(aNode^.Right);
Write(aNode^.Data : 3);
end;
END;
PROCEDURE InsertNode(VAR T : TreePtr; Item : DataType); { to create a
binary sorted tree node}
BEGIN
IF T = NIL THEN
NewLeaf(T,Item)
ELSE
IF Item < T^.Data THEN
InsertNode(T^.Left, Item)
ELSE
InsertNode(T^.Right, Item)
END;
PROCEDURE AddNode(VAR R : TreePtr);
VAR
Num : DataType;
BEGIN
Write('Number to add :');
ReadLn(Num);
InsertNode(R, Num);
END;
PROCEDURE Destroy(R : TreePtr);
BEGIN
IF R <> NIL THEN
begin
Destroy(R^.Left);
Destroy(R^.Right);
Dispose(R);
end;
END;
BEGIN { main program }
ClrScr;
Root := Nil;
REPEAT
Write('(A)dd, (P)ostorder, p(R)eorder, (I)norder, (Q)uit : ');
ReadLn(Ch);
Ch := Upcase(Ch);
Case Ch OF
'A' : AddNode(Root);
'P' : PostOrder(Root);
'R' : PreOrder(Root);
'I' : InOrder(Root);
End;
WriteLn;
UNTIL Ch = 'Q';
Dispose(Root);
END. { program }
Function to count the nodes of a Binary Tree
Function CountNodes ( R : TreePtr) :
Integer;
begin
if (R=nil) then
CountLeaves := 0
else
if (R^.left = NIL) and (R^.Right=NIL) then
CountNodes:=1
else
CountNodes := CountNodes (R^.Left) +
CountNodes(R^.Right)+1;
end;
Function CountLeaves ( R : TreePtr) : Integer;
begin
if (R=nil) then
CountLeaves := 0
else
if (R^.left = NIL) and (R^.Right=NIL) then
CountLeaves :=1
else
CountLeaves := CountLeaves (R^.Left) +
CountLEaves(R^.Right);
end;
End of Binary Tree lesson
(sorry about
the horrible program indentation - there is none! It's very hard
to do indentation in HTML. Will fix this once I learn how)