The localization of a mobile robot is extremely useful in any problem where we need to know the robotís position for navigation. Most mobile robots need three basic components to operate correctly; a representation of their environment, a method for navigating in the environment, and a method for determining its position in the environment. This paper is concerned only in the estimation of the robotís position.
A naïve approach to this problem is to use odometers to measure the displacement of the robot. This approach, known as dead reckoning, is subject to errors due to external factors beyond the robotís control, such as wheel slippage, or collision. More importantly, dead reckoning errors increase without bound unless the robot employs sensor feedback in order to recalibrate its position estimate [8].
An important issue in robot localization is obtaining domain independence. Other solutions use stored maps to navigate. In this work the robot has no previous knowledge of the domain, and creates its own map based on learned landmarks. This allows the robot to operate in any environment.
The basis of this work is to detect suitable features from a pair of stereo images. This is done automatically by the robot instead of needing a human operator to choose features as reported in [11], [9], [6]. The ability to detect suitable features allows the robot to handle real world applications including exploration.
Applications of this type of localization include exploration of new
terrain. The success of the Mars Pathfinder mission has shown the possibility
of sending unmanned robotís to explore and map distant planets. The development
of autonomous vehicles will definitely be a significant factor of many
types of exploration, especially where working conditions are hazardous
to human health.
- Vehicle Geometry and Kinematics
- Head Geometry
The Robot used in this work, shown in Figure 1, has six wheels: four
run freely on a fixed transverse axis on each corner, while the two center
wheels are motor driven. A high performance four-axis active stereo head
(see Figure 2) is mounted with its horizontal tilt axis parallel to the
floor, see Figure 4. The fiduciary head center is defined to lie
where the pan axis intersects the horizontal plane containing the tilt
axis. This point, fixed relative to the vehicle regardless of head movements,
is used to define the vehicleís location relative to a world coordinate
frame, as seen in Figure 3.
(a) (b)
Figure 1. (a)
Photo of the TRC Labmate platform. (b) Robotís Differential-drive.
The robot is assumed to always move on the xz ground-plane. Its
position and orientation are specified by the coordinates (x, z, f).
The robot-centered frame has its origin on the ground plane directly under
the head center, with its z-axis pointing to the front of the robot, x-axis
to the right, and y-axis downwards.
(a) (b)
Figure 2: (a)
TRC Bisight head. (b) Geometry of the active head. P goes vertically
through the pan axis and T goes horizontally through the elevation
axis.
(a) (b)
Figure 3. (a)
Photo of the robot, showing the mobile platform and the head. (b) The vehicleís
location in the world coordinate frame is specified with the coordinates
(x, z, f). The R coordinate frame is
carried with the vehicle.
(a) (b)
Figure 4. Mobile Platform configuration. (a) Top-view showing the position of the stereo head. (b) Robotís side-view. All dimensions are in centimeters.
The Robot consists of the TRC Labmate platform, on which the Bisight
head was mounted. Two Pulnix cameras were placed on the head to capture
images. The visual processing and localization are implemented in C++ on
two PCs. One PC hosts a frame grabber for stereo image capture and sends
commands through a communications port to the TRC Labmate Platform. The
second PC uses two communications ports to control the Bisight, PTV system.
- Approach
- Stereo Match Algorithm
- Position Estimation
The robot begins by taking a pair of stereo snapshots at its starting position. Suitable features are detected in an image using the algorithm developed by Stan Birchfield in [10], based on Kanade-Lucas-Tomasi. This algorithm will be referred to as KLT from this point forward. The KLT algorithm effectively detects features. Not all the features detected will be suitable for tracking. No attempt is made to distinguish between these at the initial stage, but they can be rejected later since they will not be tracked under the constraints of the filter.
It then attempts to find 25 features in both images and stores them.
Once they are stored, it proceeds to match features from the left image
to the right image (stereo match). The procedure to stereo match features
will be described later, now weíll focus on the general operation of the
robot. The stereo matched features are stored and then used to locate their
3D position in the robotís coordinate frame. These are added to the robotís
map. With this information, the robot can calculate its position and compare
it with its odometry reading. At this point the robot moves to a new position
and captures a new pair of stereo images, using the left image to track
features
its previous position. If some features are not successfully tracked to
the next image, it replaces the lost features with new ones. The tracked
and replaced features are used to stereo match the current image pair after
finding 25 suitable features in the right image. Then the procedure repeats
with the addition of updating the map with the replaced features. These
are added to the map once they are referenced to the fixed world coordinate
frame. The whole procedure is shown in Figure 5.
To determine which right features corresponds to its left counterpart, it is necessary to calculate the epipolar line in the right image corresponding to each left feature [7]. First the algorithm reads the list of features detected for each image. The list of features provides the coordinates (xL,yL) of each feature in the image saved on disk. Therefore they must be converted to camera pixels, since the size of the image captured by the camera is 752´ 582 pixels and the size of the image saved on disk, and used to detect features is 384´ 288.
In order to make a good stereo match a prediction of the disparity from left to right image is used. This is approximation is determined with the distance moved by the robot. This value can be obtained from the robotís odometry.
Then for each feature in the left image the distance from each right feature to the epipolar line is calculated. The list of feature distance is sorted in ascending order and then the features, which are further than an acceptable distance, filtered out. After a bit of experimentation the value of 20 was found to be sufficient. At that moment the distance between the left feature and the candidates in the right image is calculated. Next the feature with the lowest value of disparity but near a small range around the predicted disparity is chosen as the match.
Once the matched features are obtained, their 3D position in the robotís coordinate frame is calculated. This information is used together with the current estimation of the robotís position to place the features in the fixed world coordinate frame.
An overview of the steps taken to find the stereo matches is shown in
Figure 6.
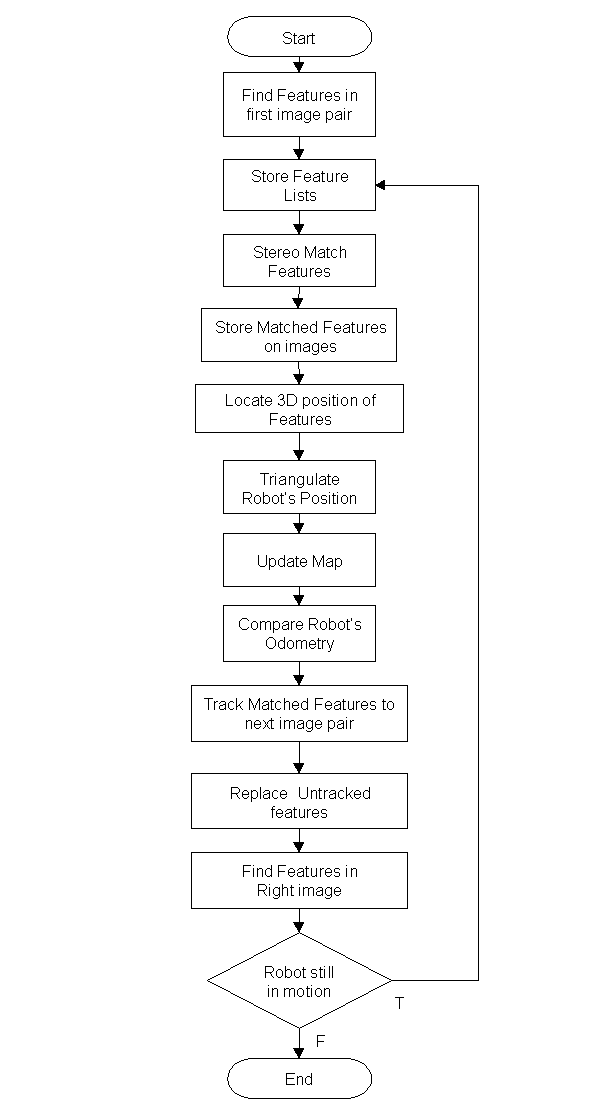 Figure
5. Flow Chart of main algorithm.
Figure
5. Flow Chart of main algorithm.
Figure 6. Flow chart of algorithm used to stereo match features.
- Image Capture
- Feature Detection
- Stereo Match
- Feature Tracking
- Experimental Environment
- Results
The Experiment conducted, consisted of taking stereo images at certain intervals, and then tracks the robotís movements. The robot was instructed to move forward 100 cms. each time. Measurements were taken (see Table 1), and the robotís odometry readings noted (see Table 2).
Table 1. Robotís location experimentally measured in the laboratory.
|
|
|
|
|
||
|
|
257.5
|
0
|
0
|
||
|
|
257.5
|
0
|
100
|
0.0
|
100
|
|
|
264.0
|
0
|
199
|
6.5
|
99
|
|
|
269.5
|
0
|
298
|
5.5
|
99
|
|
|
275.5
|
0
|
400
|
6.0
|
102
|
Table 2. Robotís location obtained by its own odometry.
|
|
q (degrees) | x (cms.) | z (cms.) | dx | dz | Distance to front wall |
|
|
0.00
|
0
|
0.1
|
721.5
|
||
|
|
359.47
|
7
|
98.5
|
7
|
98.4
|
623.1
|
|
|
359.16
|
18
|
196.8
|
11
|
98.3
|
524.8
|
|
|
358.80
|
34
|
295.0
|
16
|
98.2
|
426.6
|
|
|
358.48
|
59
|
398.4
|
25
|
103.4
|
323.2
|
To begin, the images captured are chromatic, but donít need this much information, so only the blue component con the images is stored. The images are also reduced to one quarter to improve speed in detecting features. The resulting images are achromatic (grey scale) and occupy 384´ 288 pixels, see Figure 7.
Figure 7. Stereo images captured at initial position.
Once the images were stored we attempt to find 25 features in each image.
The KLT filter to find features is constrained by the following parameters:
|
|
|
| mindist |
20
|
| window_size |
7
|
| min_eigenvalue |
1
|
| min_determinant |
0.01
|
| min_displacement |
0.1
|
| max_iterations |
10
|
| max_residue |
10
|
| grad_sigma |
1
|
| smooth_sigma_fact |
0.1
|
| pyramid_sigma_fact |
0.9
|
| sequentialMode |
FALSE
|
| smoothBeforeSelecting |
TRUE
|
| writeInternalImages |
FALSE
|
| search_range |
15
|
| nSkippedPixels |
0
|
Two images are saved Lfeat0.ppm and Rfeat0.ppm showing all the features
detected in each image.
Figure 8. Lfeat0.ppm
and Rfeat0.ppm showing the features detected by the KLT algorithm.
Next the features coordinates xL,yL and
xR,yR
are converted to camera pixels
u = xscale ´ x
v = yscale ´ y
where xscale and yscale are the ratios of the images height
and width respectively.
xscale = 752 ¸ 384
= 1.9583
yscale = 582 ¸ 288
= 2.0208
![]() Then for each feature an epipolar
line in the right image is calculated and the nearest features searched
in a range given by mindisp=20 and closest to a predicted disparity given
by:
Then for each feature an epipolar
line in the right image is calculated and the nearest features searched
in a range given by mindisp=20 and closest to a predicted disparity given
by:
where Z was the approximate distance of the features and B the inter-ocular separation of the head, 25.2 cms. (see Figure 4).
After all the matches have been found, a search is done to remove any duplicates, i.e. if two left features are matched to the same right feature.
Now we can calculate the matched features 3D position using the following
head parameters:
Fku = 1939.53;
Fkv = 2009.64;
U0 = 752/2;
V0 = 582/2;
Pp = 25.2/2; /* Horizontal offset between pan and elevation axes */
Cc = 4.0; /* Offset between elevation axis and optic axes */
Nn = 7.5; /* Offset along optic axis between vergence axes and optic
centres of cameras */
Ii = 25.2; /* Inter-ocular separation */
Hh =79; /* Height of head centre
above the ground */
And the coordinates, changed to the Fixed World Coordinate Frame. With this the position of the robot can be estimated and then the appropriate files are saved (see Figure 9). In file LMatches0.txt the coordinates of each feature are shown as well as the number of the corresponding feature in the right image. Features with no match found are given a value of Ė1. RMatches0.txt contains the features found in the right image. A value of 1 represents that it has been matched with a left feature, while Ė1 represents that no match was found.
File RealWorld0.txt contains the 3D coordinates of the matched features,
as seen in Figure 11.
(a) (b)
Figure 9. (a)
Contents of file LMatches0.txt . (b) Contents of file RMatches0.txt.
The matched features are also placed on the images and saved in PPM
format. Two files are generated; LMatch0.ppm and RMatch0.ppm, see Figure
10. Comparing the image pair in Figure 8 and Figure 10, we see not all
features detected were stereo matched.
Figure 10. Lmatch0.ppm
and Rmatch0.ppm showing matched features in each image.
Figure 11. Contents
of file RealWordl0.txt
At this moments we proceed to track the features from the previous left image to the new left image taken at the new location. If some features are not tracked to the next image, the algorithm attempts to find new features to replace them. Then 25 features are searched in the new right image, and the process repeats itself.
At the end, a new file is saved containing the history of the features
in the left image, see Figure 12.
Figure 12. Feature
Table showing the feature history in the left side.
In Figure 12, we see that in frame0 (initial location), 16 features
are stereo matched, denoted by their positive values. In frame 1, tracked
features are given a value of zero. Only 5 features are tracked from the
first image to the second. But since the algorithm searched new features
to replace the untracked, in frame 2 we are able to track 8 features. Then
only 2 features were tracked to frame 3, and finally only 1 features is
tracked to frame 4.
The laboratory wall in front of the robot during this experiment is
shown in Figure 13. The robot was placed approximately at 7 mts. from this
wall and then moved toward the wall at 100 cms. intervals. The dimensions
of this wall are shown in Figure 14. And Figure 15, shows the coordinates
of the principal features. The origin for these coordinates was placed
at the bottom-left hand corner of the wall. In Figure 16 the side- wall
is shown with its dimensions.
 Figure
13. Laboratory wall which the robot faced during this experiment.
Figure
13. Laboratory wall which the robot faced during this experiment.

Figure 14. Front wall with all dimensions shown in centimeters.
 Figure
15. Front Wall with principal feature coordinates shown.
Figure
15. Front Wall with principal feature coordinates shown.
Figure 16. Partial
view of the side-wall located to the right of the front wall shown in Figure
13.
Table 3. Experimental and Real coordinates
of the features matched and found in Figure 15
|
|
|
|||||||||
|
|
|
|
|
|
|
dx | dy | |||
|
|
210.1712
|
124.4368
|
733.8098
|
210.9
|
134.0
|
-0.7
|
-9.6
|
|||
|
|
198.1255
|
252.3184
|
707.7735
|
194.5
|
259.0
|
3.6
|
-6.7
|
|||
|
|
213.7301
|
252.5516
|
708.869
|
214.5
|
259.0
|
-0.8
|
-6.4
|
|||
|
|
281.4418
|
190.4332
|
655.2688
|
281.5
|
212.0
|
-0.1
|
-21.6
|
|||
|
|
277.3173
|
142.9643
|
724.0054
|
277.3
|
148.0
|
0.0
|
-5.0
|
|||
|
|
245.7721
|
169.7695
|
739.1494
|
244.0
|
178.5
|
1.8
|
-8.7
|
|||
|
|
277.4464
|
126.1343
|
720.4741
|
277.3
|
138.0
|
0.1
|
-11.9
|
|||
|
|
264.5356
|
167.4504
|
719.7704
|
264.9
|
178.5
|
-0.4
|
-11.0
|
|||
|
|
232.0163
|
209.9571
|
753.4997
|
232.5
|
217.0
|
-0.5
|
-7.0
|
|||
|
|
277.4094
|
185.1026
|
730.7184
|
275.3
|
194.0
|
2.1
|
-8.8
|
|||
|
|
205.1867
|
238.3834
|
710.5756
|
204.5
|
241.5
|
0.7
|
-3.1
|
|||
|
|
354.0995
|
208.4073
|
747.6114
|
356.0
|
217.0
|
-1.9
|
-8.6
|
|||
In Figure 18, Figure 19, Figure 20, and Figure 21 the 3D position calculated for the matched features are shown for each stage. As can be seen the features appear shifted to the left as the robot progresses. This indicates that the robot has moved in the positive direction of the x-axis, agreeing with the robotís odometry.
Figure 17. Image sequence of left images captured during the experiment.

Figure 18. Position of the features found and actual position of the features shown in Figure 15 at Location 0.

 Figure
19. Position of the features found and actual position of the features
shown in Figure 15 at Location 1.
Figure
19. Position of the features found and actual position of the features
shown in Figure 15 at Location 1.
Figure 20. Position of the features found and actual position of the features shown in Figure 15 at Location 2.
 Figure
21. Position of the features found and actual position of the features
shown in Figure 15 at Location 3.
Figure
21. Position of the features found and actual position of the features
shown in Figure 15 at Location 3.
 Figure
22. Features detected and stereo matched at each location. The values used
for Z are referenced to the robotís coordinate frame.
Figure
22. Features detected and stereo matched at each location. The values used
for Z are referenced to the robotís coordinate frame.
The results of robot localization are as follow:
|
|
|
|
|
|
1
|
12.8073
|
-1.2278
|
95.7116
|
|
2
|
3.0721
|
-3.5914
|
90.4321
|
These values show the robot displacement calculated at the given location.
Table 4. Statistics of Results
| Location | Features
Found and/or Replaced |
Matched
Features |
Tracked
Features |
Features used
to Estimate Position |
|
0
|
22,25
|
16
|
||
|
1
|
25,23
|
18
|
5
|
4
|
|
2
|
25,16
|
12
|
8
|
5
|
|
3
|
25,08
|
9
|
2
|
-
|
|
4
|
4
|
1
|
-
|
As seen in Table 3, the current camera calibration gives a pretty good value for the features, although as the robot gets closer, the error in the height increases. The distance to the features is acceptable, and can be seen in the files RealWorldi.txt and given the robotís distance to the front wall shown in Table 2. The inaccuracy of the cameras is probably due to the fact that the cameras were not accurately calibrated.
Attempting to re-calibrate the cameras, 16 features in the stereo pair
obtained at the starting position were used to try to find the fundamental
matrix. The 16 features and their coordinates in camera pixels are shown
in Table 5. The 8-point algorithm described in [4] was used generating
the 16 ´ 9 matrix shown in Table 6. This
matrix M is called the measurement matrix. The equation Mf = 0 was
solved where f is the fundamental matrix represented as a 9-vector.
The solution was f = 0, which is the trivial solution. And therefore
could not be used.
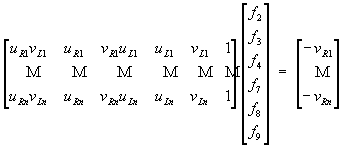 Then a 6-point algorithm
was tried, using the value in Table 6 to fill the following equation:
Then a 6-point algorithm
was tried, using the value in Table 6 to fill the following equation:
Solving the previous equation gave the following results:
| f2 = |
0.002698
|
| f3 = |
-0.799357
|
| f4 = |
-0.002669
|
| f7 = |
0.821643
|
| f8 = |
-0.866264
|
| f9 = |
-50.599253
|
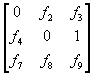 These values are part of
the fundamental matrix, denoted as the common elevation fundamental matrix.
These values are part of
the fundamental matrix, denoted as the common elevation fundamental matrix.
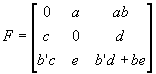 In terms of the camera parameters
we have:
In terms of the camera parameters
we have:
where
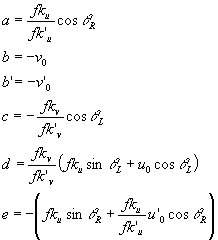
Table 5. Features used to calibrate cameras.
|
|
|
|
|
|
|
|
|
|
100
|
243
|
73
|
246
|
195.8300
|
491.0544
|
142.9559
|
497.1168
|
|
82
|
60
|
55
|
64
|
160.5806
|
121.2480
|
107.7065
|
129.3312
|
|
104
|
60
|
77
|
64
|
203.6632
|
121.2480
|
150.7891
|
129.3312
|
|
199
|
135
|
168
|
136
|
389.7017
|
272.8080
|
328.9944
|
274.8288
|
|
193
|
215
|
166
|
220
|
377.9519
|
434.4720
|
325.0778
|
444.5760
|
|
150
|
180
|
124
|
185
|
293.7450
|
363.7440
|
242.8292
|
373.8480
|
|
193
|
238
|
166
|
244
|
377.9519
|
480.9504
|
325.0778
|
493.0752
|
|
175
|
180
|
148
|
185
|
342.7025
|
363.7440
|
289.8284
|
373.8480
|
|
84
|
223
|
57
|
226
|
164.4972
|
450.6384
|
111.6231
|
456.7008
|
|
133
|
129
|
108
|
134
|
260.4539
|
260.6832
|
211.4964
|
270.7872
|
|
193
|
157
|
167
|
163
|
377.9519
|
317.2656
|
327.0361
|
329.3904
|
|
92
|
80
|
65
|
84
|
180.1636
|
161.6640
|
127.2895
|
169.7472
|
|
296
|
129
|
271
|
135
|
579.6568
|
260.6832
|
530.6993
|
272.8080
|
|
96
|
194
|
71
|
201
|
187.9968
|
392.0352
|
139.0393
|
406.1808
|
|
341
|
191
|
312
|
198
|
667.7803
|
385.9728
|
610.9896
|
400.1184
|
|
76
|
198
|
48
|
206
|
148.8308
|
400.1184
|
93.9984
|
416.2848
|
Table 6. 16 ´
9 measurement matrix.
|
|
|
|
|
|
|
|
|
|
|
27995.0539
|
70199.1237
|
142.9559
|
97350.3829
|
244111.3920
|
497.1168
|
195.8300
|
491.0544
|
1
|
|
17295.5744
|
13059.1977
|
107.7065
|
20768.0817
|
15681.1493
|
129.3312
|
160.5806
|
121.2480
|
1
|
|
30710.1906
|
18282.8768
|
150.7891
|
26340.0061
|
15681.1493
|
129.3312
|
203.6632
|
121.2480
|
1
|
|
128209.6770
|
89752.3043
|
328.9944
|
107101.2506
|
74975.4953
|
274.8288
|
389.7017
|
272.8080
|
1
|
|
122863.7722
|
141237.2019
|
325.0778
|
168028.3439
|
193155.8239
|
444.5760
|
377.9519
|
434.4720
|
1
|
|
71329.8634
|
88327.6645
|
242.8292
|
109815.9808
|
135984.9669
|
373.8480
|
293.7450
|
363.7440
|
1
|
|
122863.7722
|
156346.2979
|
325.0778
|
186358.7087
|
237144.7147
|
493.0752
|
377.9519
|
480.9504
|
1
|
|
99324.9173
|
105423.3415
|
289.8284
|
128118.6442
|
135984.9669
|
373.8480
|
342.7025
|
363.7440
|
1
|
|
18361.6874
|
50301.6552
|
111.6231
|
75126.0028
|
205806.9178
|
456.7008
|
164.4972
|
450.6384
|
1
|
|
55085.0622
|
55133.5583
|
211.4964
|
70527.5823
|
70589.6738
|
270.7872
|
260.4539
|
260.6832
|
1
|
|
123603.9154
|
103757.3045
|
327.0361
|
124493.7275
|
104504.2429
|
329.3904
|
377.9519
|
317.2656
|
1
|
|
22932.9346
|
20578.1297
|
127.2895
|
30582.2666
|
27442.0113
|
169.7472
|
180.1636
|
161.6640
|
1
|
|
307623.4580
|
138344.3918
|
530.6993
|
158135.0123
|
71116.4624
|
272.8080
|
579.6568
|
260.6832
|
1
|
|
26138.9435
|
54508.2998
|
139.0393
|
76360.6906
|
159237.1712
|
406.1808
|
187.9968
|
392.0352
|
1
|
|
408006.8184
|
235825.3667
|
610.9896
|
267191.1852
|
154434.8192
|
400.1184
|
667.7803
|
385.9728
|
1
|
|
13989.8571
|
37610.4894
|
93.9984
|
61955.9998
|
166563.2081
|
416.2848
|
148.8308
|
400.1184
|
1
|
Solving equations (1) we obtain:
| a = |
0.002698
|
| b = |
-296.256711
|
| c = |
-0.002669
|
| d = |
0.998117
|
| e = |
-0.866264
|
| b' = |
-307.815301
|
And this in turn gives us the following results:
| qL = |
89.845405
|
| qR = |
90.152938
|
| v0 = |
296.256711
|
| ví0 = |
307.815301
|
| fku = |
121.497168
|
which do are not reliable compared to the previous values used. Fku has a value that is too small. And when tested gave incorrect results. But since we are only interested in determining the robotís position from its starting point, we need only be able to determine the robotís relative movements from its initial location and not the absolute values. Therefore we can use the current camera calibration since relative measurements are mostly independent of camera calibration. And the current calibration is good enough.
The location of the robot could not be calculated at all locations. The only values obtained are for locations 0 through 2. This was due to the fact that not all tracked features could be stereo matched. The algorithms to track features and stereo match are independent and therefore do not guarantee that all tracked features will be stereo matched. In addition, the tracking algorithm only works with the left images and therefore does not know if the feature is no longer visible in the right image.
 The algorithm to stereo
match features works pretty good, but as seen in Table 4, the KLT tracking
algorithm did not find many features even though through careful examination
of the features stored in the images, we can see that more features are
still visible but were not tracked. This could be due to a great shift
in features location from one set of images to the next. Snapshots taken
at smaller intervals could provide better results, since features would
shift a smaller distance. And more features tracked would provide a better
estimate of the robotís position. Consequently in Figure 23 only the two
first legs of the robots journey is displayed. But approximating the location
of the robot by averaging all stereo matched features, gives us the results
shown in Figure 24. This is only an approximation that is reasonable since
most features found are on the front wall and therefore practically at
the same distance from the robot in the z-direction. Thus only paying attention
on the z-values, we see in Figure 24, that the movement in such direction
is pretty well tracked.
The algorithm to stereo
match features works pretty good, but as seen in Table 4, the KLT tracking
algorithm did not find many features even though through careful examination
of the features stored in the images, we can see that more features are
still visible but were not tracked. This could be due to a great shift
in features location from one set of images to the next. Snapshots taken
at smaller intervals could provide better results, since features would
shift a smaller distance. And more features tracked would provide a better
estimate of the robotís position. Consequently in Figure 23 only the two
first legs of the robots journey is displayed. But approximating the location
of the robot by averaging all stereo matched features, gives us the results
shown in Figure 24. This is only an approximation that is reasonable since
most features found are on the front wall and therefore practically at
the same distance from the robot in the z-direction. Thus only paying attention
on the z-values, we see in Figure 24, that the movement in such direction
is pretty well tracked.
Figure 23. Robot
progress as detected by vision and odometry.

Figure 24. Robot
progress including manual calculation of all locations
We have shown that robot localization is possible even without calibrated
cameras, although camera calibration would definitely improve the results.
The localization would also improve if more featured could be tracked from
one image to the next. This could be achieved by taking snapshots at smaller
intervals.
Figure 2: (a) TRC Bisight head. (b) Geometry of the active head. P goes vertically through the pan axis and T goes horizontally through the elevation axis. *
Figure 3. (a) Photo of the robot, showing the mobile platform and the head. (b) The vehicleís location in the world coordinate frame is specified with the coordinates (x, z, f). The R coordinate frame is carried with the vehicle. *
Figure 4. Mobile Platform configuration. (a) Top-view showing the position of the stereo head. (b) Robotís side-view. All dimensions are in centimeters. *
Figure 5. Flow Chart of main algorithm. *
Figure 6. Flow chart of algorithm used to stereo match features. *
Figure 7. Stereo images captured at initial position. *
Figure 8. Lfeat0.ppm and Rfeat0.ppm showing the features detected by the KLT algorithm. *
Figure 9. (a) Contents of file LMatches0.txt . (b) Contents of file RMatches0.txt. *
Figure 10. Lmatch0.ppm and Rmatch0.ppm showing matched features in each image. *
Figure 11. Contents of file RealWordl0.txt *
Figure 12. Feature Table showing the feature history in the left side. *
Figure 13. Laboratory wall which the robot faced during this experiment. *
Figure 14. Front wall with all dimensions shown in centimeters. *
Figure 15. Front Wall with principal feature coordinates shown. *
Figure 16. Partial view of the side-wall located to the right of the front wall shown in Figure 13. *
Figure 17. Image sequence of left images captured during the experiment. *
Figure 18. Position of the features found and actual position of the features shown in Figure 15 at Location 0. *
Figure 19. Position of the features found and actual position of the features shown in Figure 15 at Location 1. *
Figure 20. Position of the features found and actual position of the features shown in Figure 15 at Location 2. *
Figure 21. Position of the features found and actual position of the features shown in Figure 15 at Location 3. *
Figure 22. Features detected and stereo matched at each location. The values used for Z are referenced to the robotís coordinate frame. *
Figure 23. Robot progress as detected by vision and odometry. *
Figure 24. Robot progress including manual calculation of all locations *