http://www.oocities.org/SiliconValley/Peaks/8778/TAU_advprog.html

6 Graphs

Generally speaking, a graph is a data model just to work with a binary relation. However it has a powerful visualization as a set of points (nodes) connected by lines (edges) or by arrows (arcs). So the trees discussed above are a particular case of graphs.

6.1 Examples of graphs

Let's take several cities connected by roads.



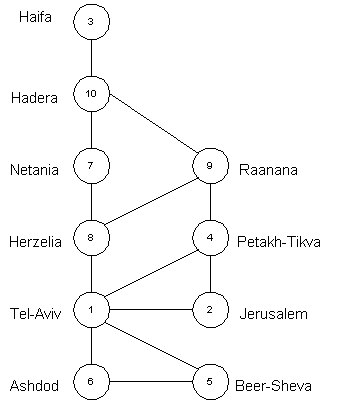
This is a graph representing connectivity of the cities. Graphs may be different: undirected and directed, weighted, etc. For example, if we take some country resided on islands (e.g. 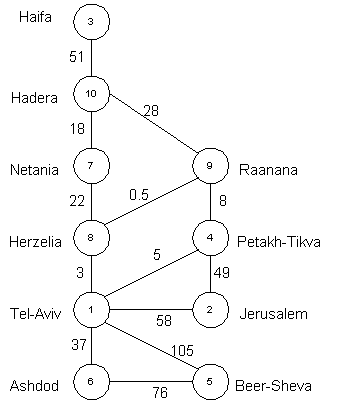Hawaiian Islands or even Great Britain or Japan) then we get such a graph consisting of several parts (each part will represent roads of 1 island but there is often no road connection between islands), so we get not connected graph. Another example: if we want to know not only the fact of connectivity between cities but also distances between them then we get weighted graph:



6.2 Formal graph definition. Kinds of graphs

Let's define some basic types of graphs and terms to manipulate with them.

A "directed graph" consists of:
  1. A set of N "nodes".
  2. A binary relation A on N. A is called set of "arcs" of the directed graph.

For example:



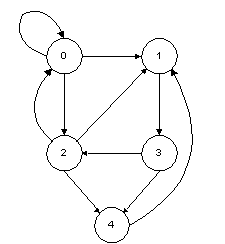
The set of arcs for this graph is:
A = { (0,0), (0,1), (0,2), (1,3), (2,0), (2,1), (2,4), (3,2), (3,4), (4,1) }
(It is written often u -> v for arc (u,v).)

For any arc (u,v) (or u -> v) v is the "head" and "u is the "tail" of the arc.
Also u is called a "predecessor" of v, and "v" is called "successor" of u.

If the head and tail of an arc is the same node then such an arc is called "loop".

As for trees, where we had some arbitrary information on each node, we can do the same for nodes of a graph. Such an attached info is called "label". Please note: we must distinguish all the nodes in a graph, so each node has some unique "name", while two or more nodes can have the same label.

A "path" in a directed graph is a list of nodes (v1, v2, ..., vk) such that there is an arc from each node from the list to the next, i.e. there is vi -> vi+1 for I = 1,2,...,k-1. The "length of the path" is k-1. (Note: any node v is a path of zero length from v to v, BUT if there is an arc (v,v) then there is also another path with length 1.)

A "cycle" in a directed graph is a path of length 1 or more that begins and ends at the same node. A "length of the cycle" is the length of the path. For our example we have cycles: (0,0), (0,2,0), (1,3,4,1), (1,3,2,4,1), etc.

A cycle can be written to start and end at any of its nodes. All such cycles are called "equivalent cycles".

A cycle (v1, v2, ..., vk, v1) is a "simple cycle" if only node v1 appears more than once there. For our example the cycle (0,2,0) is simple but the cycle (0,2,1,3,2,0) is not simple. It is clear that if there is a cycle in a graph then there must be at least one simple cycle.

If a graph has 1 or more cycles then the graph is called a "cyclic graph". Similarly if there is no cycles, the graph is called an "acyclic graph".

Let's repeat the terms we has defined for directed graphs:

It is useful sometimes to connect nodes by lines that do not have directions. Such lines are called "edges", and such graphs are called "undirected graphs". The edge {u,v} says that nodes u and v are connected (in both directions). (Note that an edge {u,u} does not make sense, so most books on graphs do not allow such edges at all.)

The definition of a "path" for undirected graph is the same as for directed one. The only thing to be noted is that edge {u,v} is the same as edge {v,u} unlike arcs in a directed graph.

We can not define a cycle like it was for directed graphs due to any edge is bi-directional. So let's start from the definition of a simple cycle: a "simple cycle" is a path of length 3 or more that begins and ends at the same node and all other nodes appear there only once. A non-simple cycle is concatenation of 1 or more simple cycles, but this thing is likely useless, so we will not use it.

Two undirected cycles are "equivalent cycles" if they consist of the same nodes either in the same orders of in reverse order.

Now we have for undirected graphs the same terms as for directed graphs excepting "edges" that are used instead of "arcs".

6.3 Graph implementations

Before we discuss various operations on graphs let's see how a graph can be implemented. There are 2 standard ways to represent a graph. The first way is more or less similar to what we had before - here we store a graph using lists. The second way is something new - there we will use matrixes.

6.3.1 Adjacency lists

The main idea here is to store for each node a list of its successors. The list may be implemented as either an array or a linked list or however else - depending on the needs for each particular case. (The graph itself is also a list of nodes.) For our example we will have the following picture of lists:

0 -> 0, 1, 2
1 -> 3
2 -> 0, 1, 4
3 -> 2, 4
4 -> 1

Please note that the list of successors must not contain the nodes themselves but references to them (by pointers or other node names). So the list of nodes must be stored separately from the lists of connections.

6.3.2 Adjacency matrices

Another approach is to store the information about connections in a matrix: if there is an arc u -> v then we will set matrix[u][v] = 1 otherwise 0. So for our example we will have the following matrix:

 | 0 1 2 3 4
------------
0| 1 1 1 0 0
1| 0 0 0 1 0
2| 1 1 0 0 1
3| 0 0 1 0 1
4| 0 1 0 0 0
It is clear that here we also must store separately the information on nodes and information about the connections.

6.3.3 Comparison of the implementations

It's a little bit problematic to compare the 2 approaches in the graph representation as the advantages and/or disadvantages of each of them is dependent on how we use the graph. The only things that are right always are:
For other actions on graphs we will distinguish sparse graphs (where the number of arcs/edges is comparable to the number of nodes) and dense graphs (where the number of arcs/edges is much greater then the number of nodes).

So if we have a sparse graph then:
If we have a dense graph then:
And so on. In fact, when you have to choose how to implement some graph, you have to think first which operations you will use on it and then make the decision.

6.4 Operations on graphs

As the 1st example let's take finding of connected components (i.e. to finds the parts of a graph that have no connections between them). The algorithm is quite simple. Firstly let's take all the nodes of the graph without any arcs. So we have each node as a separate connected component. Now we take the 1st arc in the graph and merge 2 nodes connected by this arc to one connected component. Then we take the 2nd arc and merge 2 components connected by this arc to one component. And so on. When we have considered all arcs/edges in this manner, we have all the connected components of the full graph. It is possible to prove that the running time of this algorithm is O(m * log n) (m - number of arcs, n - number of nodes). This is not the best algorithm. A better algorithm may be built using graph traversing methods. Moreover the most of algorithms for graphs are based on graph traversing.

6.4.1 Graph traversing

There are 2 ways to traverse a graph. They are called:

6.4.1.1 Breadth first search and traversal

In breadth first search we start at a node v and mark it as having been reached. We say that a node has been explored when we has visited all nodes adjacent from it. All unvisited nodes adjacent from v are visited next. These are new unexplored nodes. The first node on this list is the next to be explored. Exploration continues until no unexplored node is left. So the list of unexplored nodes operates as a queue. Let's write this function in pseudocode (not in C):

BFS( int v) /* BFS stands for "breadth first search" */
{
	Queue q(SIZE);
	int u = v;
	visited[v] = 1;
	do
	{
		/* here is the place where we will be with */
		/* each node of the graph as u */
		for all nodes w adjacent from u
		{
			if( visited[w] == 0)
			{
				q.put(w); /* add to the queue */
				visited[w] = 1;
			}
		}
		if( q.empty()) /* no more unexplored nodes */
			return;
		u = q.get(); /* get the 1st unexplored node */
	} while( 1);
}
The BFS() function visits all nodes reachable from the node v. If we are not sure that our graph is connected then we have to write a function more to ensure visiting of all nodes:

BFT( int SIZE) /* BFT stands for "breadth first traversal" */
{
	int n;
	boolean visited[SIZE];
	/* first we mark everything as not visited */
	for( n=1; n<=SIZE; n++)
		visited[n] = 0;
	/* and to use the BFS() for not visited nodes */
	for( n=1; n<=SIZE; n++)
		if( !visited[n])
			BFS(n);
}
Please pay attention that the running time of this algorithm is dependent on graph representation: if we have a graph with n nodes and m arcs then for adjacency matrix we have O(n2) while for adjacency lists we have O(n+m). Nevertheless reminding that for a full graph (where all nodes are connected to all nodes) we have m = n2/2+n (just imagine its adjacency matrix), the representations become the same when we deal with a dense graph.

6.4.1.2 Depth first search and traversal

Another method to traverse graph is a "depth first search". It differs from a breadth first search in that the exploration of a node v is suspended as soon as a new node is reached. At this time the exploration of the new node u begins. When this new node has been explored, the exploration of v continues. Such a procedure may be easily written recursively (again: this is pseudocode not C):

DFS( int v) /* DFS stands for "depth first search" */
{
	visited[v] = 1;
	for all nodes w adjacent from v
	{
		if( visited[w] == 0)
			DFS( w);
	}
}
Again this function will visit all nodes reachable from node v. So to ensure visiting of all nodes in the graph we have to write a function DFT(), which is similar to the BFT() discussed above.

The running time here is the same as for breadth first search.

Please note that the breadth first search algorithm is based on a queue of nodes while the depth first search algorithm is based on a stack (this fact is hidden by implementation via recursion).

6.4.2 Exercise 6

6.4.3 Applications of the graph traversing and other important algorithms on graphs

6.4.3.1 Connected components find

A problem requiring to find connected components of a graph (or one of them - starting from some definite node) then we already have several solutions for it: any graph traversal algorithm (either DFS or BFS) can be used for this.

Please note that to solve this problem the graph must be treated as undirected (even if it is directed).

Running time (as we saw) of this task will be O(n+m).

6.4.3.2 Reachability test

A natural question often appearing for directed graphs: is there a path from node u to node v? Or in more general form: if to start from node u then which nodes can be reached?

The simplest way to solve this problem is (like in the previous case) to use one of the search algorithm (either DFS or BFS) discussed above.

Naturally the running time of this task will be again O(n+m).

6.4.3.3 Topological sort for undirected acyclic graphs

Suppose we know that a directed graph is acyclic. We want to find such list of its nodes (v1, v2, ..., vk) that for each edge vi -> vj the node vi goes in the list before the node vj.

There are many examples when such a task must be solved. Let's take one of them - a simple case of planning task: you have a list of tasks, and you know that some tasks are dependent on completion of some certain other tasks. If you represent tasks as nodes and the dependencies between them as edges then after getting such a "sorted" list of task you get the order, in which the tasks can be performed.

The algorithm solving this problem is based on DFS(). Let's start DFS() from some node vi and store node in a stack in postorder manner: 
DFS( int v) /* DFS stands for "depth first search" */
{
	visited[v] = 1;
	for all nodes w adjacent from v
	{
		if( visited[w] == 0)
			DFS( w);
	}
	push node v into the stack
}
After the 1st run of DFS() we got in our stack all nodes reachable from the node vi in the desired order (i.e. the more "far" nodes have been pushed into the stack first). Repeating the same DFS() (in a manner of DFT()) for not visited nodes we fill our stack with all nodes in topologically sorted order.

Again we have the same running time (the running time of DFT()).

6.4.3.4 Minimal spanning tree find (Kruskal's algorithm)

Let's take an example. Some big company has offices in several locations. The company have to rent dedicated data transmission lines from the phone company in order to provide good communication between the offices. We suppose that such lines exist between most of the locations although not between all (so we have graph of possible communications). Each line has its own cost, which may depend on distance (some locations are closer than others), kind of line (lines may be aerial, ground, sattellite, whatever else), etc. I.e. each edge in our graph has its weight. But we know that if we connect offices A<->B and B<->C then we can suppose that we connected also A<->C. We want to rent lines with minimal summary cost.

In other words we have to break in our graph some edges and the summary of weights of the remained edges must be minimal.

This task is called "finding of minimal spanning tree". There are several algorithms solving this task. We will discuss one of them, which is called Kruskal's algorithm.

The algorithm is:
  1. First of all, we take the list of all edges of the graph and sort the list in order of increasing edges' weights.
  2. Then we take the edge with the smallest weight. The 2 nodes connected by this edge start to build one connected component.
  3. Now we take edges in order of increasing their weights. for each edge we look:
  4. We continue the previous step until we have edges in our sorted list. Then we got the minimal spanning tree for our graph (or several trees if the graph was not connected).
So if you have the graph:


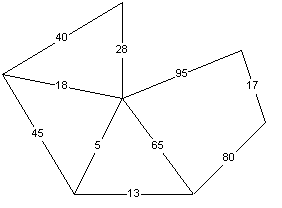
Then the order of edges will be:


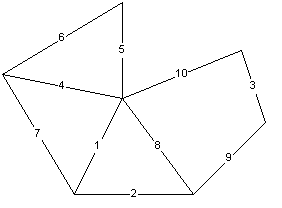
And the resulting minimal spanning tree:


This algorithm works for undirected weighted graphs.

(The prove why the algorithm works is omitted here and may be found in any appropriated book.)

The running time of Kruskal's algorithm is O(M*logN), where M is number of edges and N is number of nodes in graph.

"Greedy" algorithm paradigm.

Kruskal's algorithm is a good example of a greedy algorithm, in which we make a series of decisions, each doing what seems best at the time. The "local" decisions are which edge to add to the spanning tree being formed. In each case we pick the edge with the smallest weight that doesn't violate the definition of "spanning tree" by completing a cycle.

Often the overall effect of the "locally" optimized decisions is not "globally" optimum. However, the Kruskal's algorithm is one of algorithms, for which it can be shown that the result is globally optimal.

6.4.3.5 Shortest path find (Dijkstra's algorithm)

One of the "classic" tasks on graphs is: we have a graph (either directed or undirected) with labels on its arcs (edges) representing the "length" of each arc (edge). (Just recall the 1st example of graph - map of roads.) The task is to find the "shortest" path (or minimal "distance") between 2 nodes. The "distance" may have various meaning for each particular task, even for the original task on road map graph, such a "distance" may be: geographical distance, time to go, cost of the way, etc.

Anyway the distance is the sum of the labels on arcs (edges) along the path. The minimal distance from node u to node v is the minimum of the distance of any path from u to v.

One of the algorithms solving this problem is Dijkstra's algorithm. It finds the minimal distance from one given node (source node) to all other nodes of the graph. So, if the desired result is the distance from one node u to another node v, then the solution is to apply Dijkstra's algorithm with u as the source node and stop when it deduces the distance to v.

During its work the algorithm will find the minimal distance from the source nodes to other nodes. So at any moment we will have some nodes with already known minimal distances - such nodes are called settled nodes (even in the very beginning there is one node - our source).

Also at any moment we will have nodes, for which the minimal distance is unknown yet (well, when the algorithm finishes this set is empty). For these "unsettled" nodes we know so called special path, which starts at the source node, goes through settled nodes only and at the last step jumps out of the settled "region" to the node.



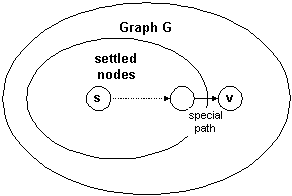
The algorithm is: So if we take our example of Israel cities and distances along the roads between them:



Then the steps of Dijkstra's algorithm for the source node Herzelia will be as in the table below. This table represents values of dist(u) on each step (values changed on a step are shown in bold):

Step 1 Step 2 Step 3 Step 4 Step 5 Step 6 Step 7 Step 8 Step 9 Step 10
Ashdod INFINITY INFINITY 40 40 40 40 40* 40* 40* 40*
Beer-Sheva INFINITY INFINITY 108 108 108 108 108 108 108 108*
Hadera INFINITY 28.5 28.5 28.5 28.5 28.5* 28.5* 28.5* 28.5* 28.5*
Haifa INFINITY INFINITY INFINITY INFINITY INFINITY 79.5 79.5 79.5 79.5* 79.5*
Herzelia 0* 0* 0* 0* 0* 0* 0* 0* 0* 0*
Jerusalem INFINITY INFINITY 61 57 57 57 57 57* 57* 57*
Netania 22 22 22 22 22* 22* 22* 22* 22* 22*
Petakh-Tikva INFINITY 8.5 8 8* 8* 8* 8* 8* 8* 8*
Raanana 0.5 0.5* 0.5* 0.5* 0.5* 0.5* 0.5* 0.5* 0.5* 0.5*
Tel-Aviv 3 3 3* 3* 3* 3* 3* 3* 3* 3*

6.4.3.6 Clique find. NP-complete tasks.

First of all, a couple of definitions more: There is an important task, which can be formulated so: This task is called maximum clique problem.

A corresponding decision problem is to determine whether graph G has a clique of size k (for some given k). ("Corresponding" means that if we can solve one of the tasks then we can solve another task as well.)

Let's look at an example when this problem must be solved. Let's take another aspect of planning problem: we have a set of tasks (nodes) and dependencies between them (edges). The existence of a dependence between 2 tasks means that these 2 tasks can not be performed simultaneously. Also suppose that all tasks have the same duration and there is no limitation on number of simultaneously performed independent tasks. Now we can solve the problem by building another graph: we create an edge between nodes, where was no edge (dependence), and we remove edge between previously connected nodes. So we get graph of task "independence". Now we can find the maximum clique in this graph - the nodes in this clique will be the tasks, which we will perform first. Then we delete the found clique from our graph and repeat the maximum clique find for the rest of graph, an so on.

Here is the end of good news. Bad news are that there is no known polynomial time deterministic algorithm for this problem. Some important notes: Another such problem is so called Travelling Salesman Problem: you have a graph of cities and roads between them, you have a salesman, who have to visit some of the cities, each city once only. You must find the best (e.g. shortest) way for the salesman. This "simple" task is also not solvable in polynomial time.

Such problems are called NP-complete. There are 14 known NP-complete problems; list of them may be found in any appropriate book. The number 14 means that there are 14 REALLY different problems, but there is a lot of problems, which may be transformed to one of these 14 (like our 2 variants of clique task). Once again: it is not proven that they are not solvable in polynomial time, but there is no such a solution known.

It is very important, when you try to solve some particular problem, to check: perhaps the problem is NP-complete? If it is then it may be solved for very small size only, and you have to find another approach for solution (may be not exact but some approximate solution?).

6.5 Important graph applications

Among other examples of graph application there is a lot tasks more, where graphs are the best (and often the only) way to solve them. In fact any task, where you have some instances and binary relationship between them, seems to be represented by graphs in the most handy and clear way. There is indefinite amount of such examples: Some of such representations are so important that they have wide field of application and even their own names.
For example, if you have some system (system may be a physical system, or program, or whatever else), which at any moment can be in one of some definite states, and you know all possible transformations of the system from a state to another state, then the best representation of such a system is so called Finite State Machine: a graph with nodes - possible states, and arcs - possible transformations between states.

As a conclusion: a graph theory is a vast science, and this course touched the very basic issues only. Anyway having the understanding of the main approaches and possible problems here should help to find solutions for the real specific tasks (for example, in books).