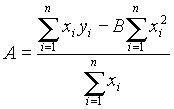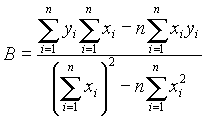Doppio Ponte di Kelvin

Doppio Ponte di Kelvin

Misurare: Rx, di valore molto piccola(dell’ordine delle resistenze di contatto). Utilizziamo il doppio Ponte di Kelvin anziché Wheatstone, perché in esso le resistenze di contatto amperometriche non intervengono nell’equilibrio del ponte perché interessano solo la maglia d’alimentazione. Le resistenze di contato voltmetriche (» mW ) sono poste in serie a resistenze più grandi e quindi possono essere trascurate. Inoltre tramite, l’utilizzo di un metodo di zero, o confronto, ottengo un’elevata precisione.

Operando la trasformazione triangolo stella tra le resistenze R1’ R2’ ed R il ponte di Kelvin assume la struttura del Ponte di W. Se R1/R1’=R2/R2’ si arriva alla seguente relaz. di equilib. R1Rc=R2Rx da cui si ricava Rx.

Dato che Rx è un filo di cui conosciamo l, d,r , possiamo ricavare Rx teorico Rx=(r *l)/(p d²/4)=4,68 mW

(r =0.0178 m W m).

Per avere una buona precisione della misura le resistenze che caratterizzano il ponte devono avere valori elevati rispetto alle resist. di contat. voltmetriche. Per semplicità scegliamo R₁=R₁’ ed R₂=R₂’ . Con E=6V si regola il reostato del bancone in modo da avere I=2 A. In base al valore teorico di R_X, fisso R₁=46 W , R₂=10 W . Si verifica l’equilibrio con il tasto T a zavorra nulla. Se vediamo delle variazioni nel galvanometro si varia R₁ ed R₁’ (resistori a decadi) uguali. Raggiungo l’equilibrio con R₁ = 48 Per cui risulta R_x=R₁/R₂*R_c= 4,8 mW , dato che R_c=10^-3W L’incertezza totale relativa della misura è I_Rx=I_R1+I_R2+I_Rc+e s l’errore di sensibilità e s =D R_x/R_x*d l /D l dove d l =1/2 e D l =1. Vista la proporzionalità fra R_x ed R₁ (R_x=R₁/R₂*R_c), vario R₁ e quindi R₁’ fino a spostare l’indice del G di 1 tacca, per cui si ha D R₁= 56-48 e risulta e s =83,3*10^-3.

Inoltre I_R1=I_R2 =0.0005, I_Rc=1*10^-5 per cui I_Rx= 0,084 per cui l’incertezza assoluta risulta R_xI_Rx=4,2*10^-3 0,084=0.35*10^-3

Allora R_x=4,8± 0,35 mW .

Possiamo verificare cosa succede se rifacciamo la misura con rapporti di resistenze 10 volte maggiori. Si raggiunge l’equilibrio quando R₁ =R₁’ = 470 e si ha R_x=4,7 mW . D R₁(variaz. della resistenza affinché si abbia uno spostamento dell’indice di G di una tacca)=620-470, e s =150/470*0,5=159,5*10^-3, I_Rx=5*10^-4+5*10^-4+1*10^-5+159.5*10^-3= 160,5*10^-3. R_xI_Rx=0,75*10^-3. Allora R_x=4,7± 0,75 mW .

Q_A e Q_V

Alimento il circuito con un onda sin di freq. f=280 KHz, porto il circuito in risonanza variando la capacità. Poiché la condizione di accoppiamento lasco non è così verificata, (infatti variando le capacità varia anche la tensione al primario prelevata ai capi della R tramite sonda e non con cavetto) allora riduco la frequenza e vario la capacità ricercando una nuova condizione di risonanza, finché f_r=226,4 KHz, C_r=1097 pF in corrispondenza ai quali l’accoppiamento tra primario e secondario risulta lasco. Posso ora scollegare la sonda, (la condizione di lasco sarà mantenuta a maggior ragione). Per determinare Q_A applico il metodo per variazione di reattanza, ossia lascio inalterata la frequenza e diminuisco ed aumento la capacità in modo da trovare i due valori per i quali la tensione risulta ridotta di 3 bB rispetto al valore massimo ottenuto alla risonanza.

C₁=1065,5 pF, C₂=1114 pF. Q_A=(C₂+C₁)/(C₂-C₁)=44,94. Regolo nuovamente la capacità al valore 1097 pF e cerco f₁ ed f₂ tali che il segnale di uscita si riduca di 3 dB e troviamo f₁=224,8 KHz, f₂=228,9 KHz, Q_V=1/2*(f₂+f₁)/(f₂-f₁)=55,86.

Ripeto la procedura sostituendo al cavetto con il quale avevo prelevato il segnale dal secondario la sonda.

Metodo per variaz. di reattanza con sonda.

f_r=223,8 KHz, C_r =1210 pF, C₁ =1185 pF, C₂= 1231 pF, Q_{A sonda} =52,5

Metodo per variaz. di freq. con sonda

C_r=1210 pF, f_r=223,8 KHz, f₁=222,0 KHz, f₂=225,9 KHz, Q_{V sonda}=57,4.

E’ interessante notare che:

Q_{V sonda} » Q_{V cavetto} , Q_{A sonda} > Q_{A cavetto} ciò è coerente con le mie aspettative infatti Q_{V s} e Q_{V c} devono essere quasi uguali perché valori caratteristici del circuito. Dato che C₀’ è in parallelo a C allora C₀’ è uguale a C₀+C_m. Ma C_{m cavetto}>20 pF e C_{m sonda}=11 pF per cui dalla seguente formula Q_V = Q_A+2 C₀’/(C₂-C₁) segue Q_As>Q_Ac.

Lo sfasatore

Lo scopo della nostra esperienza è la misura della differenza di fase tra un segnale preso come riferimento,

(che andrà sia al canale A dell’oscilloscopio sia all’ingresso di un circuito sfasatore) , e la sua uscita dallo sfasatore. Lo schema dello sfasatore risulta:

Per prima cosa precisiamo che è corretto parlare di sfasamento j tra due segnali espresso in gradi o radianti solo nel caso i due segnali siano alla stessa frequenza e siano sinusoidali. Oppure se un dei due segnali sono ottenuti uno dall’altro.

Nel nostro caso invieremo il nostro segnale sia all’oscilloscopio Canale Ya sia ad un circuito sfasatore e quindi collegheremo l’uscita dello strumento sfasatore all’ingresso Yb.

Lo schermo dell’oscilloscopio presenterà i due segnali, identici ma sfasati, e tramite l’asse dei tempi posso misurare l’angolo j _m = 2p D T/T=2p D Tf

Mentre j _rc =arctg (w RC)

Quindi ottengo D j =j _m-j _rc

Prendo f = 400 kHz = (1/2p RC) ottengo

R = 796 W

C=0,001 m F

Trovo D T=0.44 m s

j _rc =arctg (w RC)= 45⁰ = 1.107 rad

j _m = 2p D T/T=2p D Tf=1.106 rad

D j =j _m-j _rc=1*10^-3

Prendo f = 200 kHz = (1/2p RC) ottengo

R = 796 W

C=0,001 m F

Trovo D T=0.7 m s

j _rc =arctg (w RC)= 45⁰ = 0.785

j _m = 2p D T/T=2p D Tf=0.879

D j =j _m-j _rc=0.094

L’incertezza delle misure fatte risulta essere data dalla somma dell’incertezza con cui valuto D T che è dell’ordine di 10^-3(incertezza dell’oscilloscopio) e dell’incertezza di f che è quella del frequenzimetro che è dell’ordine di 10^-6

Quindi l’incertezza totale è circa 10^-3

Tempo di risposta t_r

Scopo della misura è di misurare il tempo di risposta di un circuito accordato, ossia l’intervallo di tempo necessario affinché l’inviluppo della risposta ad un segnale sinusoidale modulato da un gradino, si porti dal 10% al 90 % del valore massimo ( o di regime ).

Una volta che il circuito arriva a regime, il transitorio viene mascherato dalla forma d’onda, e risulta impossibile valutarlo. Allora al fine di visualizzare con permanenza questo transitorio di salita, che risulta molto breve, mando al circuito un’onda radaristica costituita da pacchetti di una sinusoide con frequenza f_r , pari alla freq. di risonanza, che si susseguono ad intervalli regolari.Cioè rendo il transitorio periodico

La frequenza f_r della sinusoide deve essere tale da verificare la condizione di accoppiamento lasco tra il primario ed il secondario del nostro circ. accordato.

Per trovare tale condizione di accoppiamento, dopo aver collegato il circuito accordato tramite la sonda all’oscilloscopio, lo alimento con un onda sin di freq. f=280 KHz, porto il circuito in risonanza variando la capacità. Poiché la condizione di accoppiamento lasco non è così verificata, (infatti variando le capacità varia anche la tensione al primario prelevata ai capi della R tramite sonda e non con cavetto) allora riduco la frequenza e vario la capacità ricercando una nuova condizione di risonanza, finché f_r=250,0 KHz, C_r=1036 pF in corrispondenza ai quali l’accoppiamento tra primario e secondario risulta lasco. Posso ora scollegare la sonda, (la condizione di lasco sarà mantenuta a maggior ra gione). A questo punto procedo a generare l’onda radaristica, e la applico all’ingresso del circ.

L’onda radarist. viene generata mediante l’utilizzo del generatore di funzione, collegando l’uscita AUX OUT all’ingresso TRIG-IN. Il primo fornisce un dente di sega con una frequenza indipendente da quella del segnale principale. Il selettore di funzione viene spostato nella posizione GATED e tramite il TRIG LEVEL si comanda l’istante di sgancio. In questo istante il dente di s. incrocia il livello di sgancio facendo partire la forma d’onda selezionata, alla freq. f_r prefissata, la cui durata si estende sino alla fine del dente di sega. La distanza tra i pacchetti viene variata agendo sulla manopola SWEEP TIME, che gestisce la durata del dente di sega. E’ importante fare in modo che le varie risposte del circuito accordato non si sovrappongano. Per ottenere una visualizzazione ottimale e completa, sincronizzo l’oscilloscopio sul dente di sega del generatore di forme d’onda e procedo ad ingrandire a tutto schermo la parte iniziale di uno dei pacchetti visualizzati. Utilizzando quindi il DTB si ottiene una maggiore precisione nella misura del tempo di risposta.

Il segnale che ritrovo in uscita, ha un andamento del tipo:

V_U=QV_i(1-e^-t/t ) con t =2L/R

f₁=247,7 KHz , f₂=252,5 KHz , B=f₂-f₁=4,8 KHz

f_r=250,1 KHz, dove f₂ ed f₁ , sono le freq. per cui si ha l’attenuazione di 3 dB del segnale di uscita, con per cui

t_{r indiretto}=0,7/B=145,83 m sec

t₁=75,20 m sec , t₂=224,95 m sec ,

t_{r diretto}=t₂-t₁= 149,75 m sec

Misura di E_x

Lo scopo della misura è di valutare il valore di una f.e.m. E_X mediante il confronto con una pila campione E_C. Il metodo utilizzato è quindi il metodo potenziometrico (o di zero). verifico che il tasto T in serie al G sia aperto. Verifico inoltre che la zavorra in serie al G sia al valore massimo.

Per semplificare l’esperimento fisso la corrente del circuito di alimentazione sul valore 1 mA leggendo l’indicazione del galvanometro. Per fissare con maggiore precisione tale valore, procedo come segue. Conoscendo il valore della pila campione E_C=1,018161 Volt, fisso il valore di R₁=1018 W ed R₂=10092 W (complementare a 11110 W ). In questo modo picchettando sul tasto di chiusura del circuito, dopo aver azzerato gradatamente la zavorra, agendo sul potenziometro del circuito di alimentazione mi assicuro, tramite metodo di zero, che la corrente che vi circoli sia 1 mA, poiché ciò si verificherà quando la caduta su R_1C è uguale a E_C.

Fissata allora la mia corrente I=1mA rimetto la zavorra (R_G) al massimo.

Con E_C ed E_X sconnesse, pongo le resistenze ai valori R₁=1500 W (valore della E_X scritto sull’involucro) ed R₂=9610 W . E’ importante che la somma di R₁ ed R₂ rimanga costante per tutto l’arco della misura.

Commuto ora su E_X, e abbasso gradatamente il valore della zavorra, fino ad azzerarla, correggendo contemporaneamente il valore di R₁, fino a che l’indice del G segni lo zero. Dato che la corrente che attraversa R₁ è 1 mA, il valore letto su R₁ mi da direttamente la tensione di E_X per mille (reale), come si ottiene dalla relazione E_X=E_C/R_1C*R_1X dove R_1C =1018 W .

Ottengo così un valore finale di R_1X=1591 W .

Calcolo ora l’errore di sensibilità che commetto su R_1X. Vario R₁ fino a leggere una variazione dell’ago di G di una tacca. Ottengo così il valore R_1X’=1593 W , per cui e s =D R_1X/R₁*dl /D l , dove dl è la minima variazione discernibile che valuto ½ tacca. Allora

e s =2/1593*0,5=6,28E^-4

L’incertezza relativa sul valore E_X è data da I_EX=I_R1X+I_R1C+I_Ec+2e s =5*10^-4+ 5*10^-4+2*6,27E^-4= 2.24*10^-3

Incertezza assoluta = I_EX* E_X=3.5 *10^-3

Segue E_X=1,591± 3.5 *10^-3Volt

Verifica dell’asse dei tempi dell’oscilloscopio

Lo scopo della prova è verificare se l’errore che si commette sull’asse dei tempi è minore del 3% dichiarato dal costruttore.

Tale verifica si effettua utilizzando un generatore di segnali ed un contatore. Quest’ultimo ha una precisione pari a 10^-6, ma poiché il generatore ha precisione di 10^-4, allora il valore visualizzato su display del contatore sarà significativo fino alla quarta cifra, le altre saranno del tutto prive di significato. Tutto ciò garantisce comunque la correttezza della misura infatti la stabilità del complesso , generatore + contatore, sarà comunque maggiore di quella dell’oscilloscopio. Per il quale il costruttore garantisce una precisione dell’ordine di 10^-3 (incertezza sulla terza cifra).

Il contatore andrà a valutare quanti impulsi genera il segnale f_X in un intervallo di tempo opportuno. La durata di tale intervallo, detto tempo di porta, può essere regolata dall’esterno. È opportuno, in un primo momento, valutare l’ordine di grandezza della freq. incognita scegliendo la posizione AUTO, in corrispondenza alla quale lo strumento sceglierà un tempo di apertura tale da evitare la situazione di OVERFLOW. Dopo aver letto l’ordine di grandezza della freq. visualizzata, si può commutare su un tempo di apertura manuale tra le possibili scelte (0,1 sec/1 sec/10 sec). Questo procedimento mira ad aumentare la precisione della misura

Per effettuare la misura procedo nel seguente modo. Fisso una frequenza di partenza sul generatore di segn. Visualizzo sullo schermo dell’oscilloscopio un numero di periodi elevato, da rientrare nelle otto divisioni più interne allo schermo, ed in modo da mantenere distinguibile un periodo dall’altro. Maggiore è il numero di periodi che leggo, maggiore sarà la precisione della mia misura. Inoltre considero solo gli otto quadranti più interni allo schermo,infatti è in questi che il costruttore mi assicura una precisione del 3%. Vengono escluse sia il primo sia il decimo intervallo infatti qui non è detto che vi sia tale precisione. Infatti nel primo intervallo abbiamo un incertezza legata allo sgancio ed al transitorio, nell’ultimo un’incertezza legata al ritorno del dente di sega

Misuro ora tramite il Delay Time Base la durata degli n-periodi e la divido per il numero di questi, ottenendo così la durata di un singolo periodo, il cui inverso mi darà il valore della frequenza del segnale applicato all’ingresso dell’oscilloscopio.

f_{1 letta}=19,96 KHz

16 periodi visualizzati = 0,800e^-3 sec

1 periodo = 0,050e^-3 sec

f₁ _misurata=20,00 KHz

e%= (20,00-19,96)/20,00*100= 0,20%

f_{2 letta}=203,2 KHz

16 periodi visualizzati = 7,97e^-5 sec

1 periodo = 4,98e^-6 sec

f₂ _misurata=200,8 KHz

e%= (203,2-200,8)/203,2*100= 1,18%

f_{3 letta}=500,4 KHz

20 periodi visualizzati = 4,01e^-5 sec

1 periodo = 2,00e^-6 sec

f₃ _misurata=498,7 KHz

e%= 0,33%

f_{4 letta}=2,002 MHz

16 periodi visualizzati = 8,00e^-6 sec

1 periodo = 0,50e^-6 sec

f₄ _misurata=2,000 MHz

e%= 0,09%

L_V e C₀

Le misure in oggetto, hanno lo scopo di determinare L_V e C_0,

Consideriamo ora l’espressione della pulsazione di risonanza ,dove C_m è la capacità dovuta agli strumenti di misura (sonda + oscillosc.) e C è la capacità variabile dall’esterno.

Pongo C₀+C_m=C₀’ e poiché w _r=2p f_r si ha (2p f_r)²=1/(L_V(C_r+C₀’)) segue

(2p f_r)² L_vC_r+ (2p f_r)² L_VC₀’ =1

1/f_r²=4p ²L_VC_r + 4p ²L_VC₀’ questa è l’equazione di una retta nel piano (C_r,1/f_r²).

Anche se due punti sono sufficienti per determinare la retta e con essa i valori di L_V e C₀’ , la soluzione sarà affetta da una notevole incertezza quindi si ricorre ad una interpolazione lineare adoperando il metodo della regressione lineare. Per cui si individua un campo di risonanza cioè si ricercano diversi valori di freq. di rison. per diversi valori di capacità, effettuando quindi le misure, muovendoci in un intorno di f_r tale che la condizione di accop. lasco resti verificata. La misura di C₀’ verrà effettuata prelevando il segnale dal circuito tramite una sonda di cui è noto il valore della capacità(11 pF), per cui C_m = 11 pF + 3 pF (oscillosc.).

I valori di C_r esatti vengono ottenuti come semisomma dei due valori che di disaccordo in corrispondenza ai quali il segnale di uscita si riduce di 3dB. Questo ci permette di evitare l’incertezza relativa alla zona piatta della curva di risposta.

Capacità in pF.

F_r^(KHz)	C₁	C₂	C_r	1/f_r²
215	1162	1128	1195	2.163e^-11
212	1208	1237	1222	2.224e^-11
216	1118	1204	1160	2.143e^-11
207	1296	1318	1308	2.333e^-11
200	1340	1406	1376	2.5e^-11
195	1442	1480	1461	2.629e^-11

1/f_r²=4p ²L_VC_r + 4p ²L_VC₀’ y=Bx+A

dal calcolatore risulta A=1.639e^-12 B=16,84e^-3

Dove y_i=1/f_{r i}² e x_i =C_{r i}

B=4p ²L_V allora L_V = B/4p ²=426 microH

A=4p ²L_V(C₀+C_m)

C₀+C_m=97.5 pF

C₀=97.5-11=86.5 pF