Avendo un segnale se esso è trasformabile secondo Fourier ,possiamo esaminare la parte immaginaria e la parte reale avremo così lo spettro di fase e lo spettro di ampiezza.

Per quando riguarda le notizie storiche l’A.S ha avuto il suo sviluppo durante la seconda guerra mondiale grazie agli studi radaristici.

Il Radar funziona grazie alle onde elettromagnetiche che vengono riflesse dai metalli. Infatti per un’onda un metallo costituisce un cortocircuito e quindi viene riflessa.

Il problema sta nel rilevare propri questo eco.

L’onda deve essere di grossa potenza (MW) ed irradiata per un tempo brevissimo ad alta frequenza.

L’impulso di ritorno è fortemente attenuato ed è anche distorto. Nasce allora il problema dovuto alla costruzione di un ricevitore, e quindi nasce il problema di guadagno-ampiezza di banda.

Il ricevitore deve essere ottimizzato a ricevere al meglio possibile la potenza che si manifesta nel lobo centrale dello spettro.

Il segnale d’invio è caratterizzato dal prodotto di una sinusoide per un impulso

 Ora per verificare se il trasmettitore funziona bene devo utilizzare l’A.S poiché non è possibile visualizzare la forma d’onda nel dominio del tempo in quanto essendo t <<T l’impulso verrebbe mascherato dietro l’ampiezza della traccia.

Gl’impulsi di ritorno chiaramente sono diversi da quelli inviati , sono deformati, più piccoli, non è detto che siano simmetrici. E’ stato pertanto necessario andare a studiare le caratteristiche medie degli spettri che tornavano indietro .

L’ampiezza di banda per il ricevitore non è detto che sia ancora 2/t ma potrebbe essere maggiore.

Oggi possiamo definire l’analizzatore di spettro quello strumento che si deve impiegare per rilevare le prestazioni utili di un segnale quando questo non può essere rappresentato adeguatamente nel dominio del tempo.

Un segnale risulta difficilmente analizzabile nel dominio del tempo quando è fortemente modulato .

Se prendo un segnale modulato in frequenza risulta inaccessibile ad un oscilloscopio.

Quindi per coprire lo studio di tutte le frequenze abbiamo

ANALIZZATORI D’ONDA

ANALIZZATORI DI DISTORSIONE

ANALIZZATORI DI SPETTRO

ANALIZZATORI DI FOURIER

L’analizzatore di spettro esamina il modulo della trasformata di Fourier di un segnale che ha uno spettro a righe.

Gli analizzatori di spettro si dividono in due categorie:

SWEPT FRONT-END (a scansione frontale)

SWEPT IF (a frequenza intermedia scandita)

Il primo ( pag.205)

Nello schema si nota un mescolatore ove entra un segnale a frequenza f_x ed una frequenza f_l0 proveniente da un oscillatore accordabile in tensione nel quale mandiamo un dente di sega. Di conseguenza la frequenza fornita dall’oscillatore varierà da un min ad un max .

Mescolando la f_x con la f_l0 otteniamo una forma d’onda modulata in frequenza con legge triangolare che alimenta un amplificatore a frequenza intermedia.

All’uscita dell’amplificatore mettiamo un rivelatore per modulazione di ampiezza dal quale esce un segnale del tipo . Che si verifica nell’intorno di una certa tensione per la quale si realizzano le condizioni di battimento.

In uscita al mescolatore avrò

f_l0 + f_x

f_l0 - f_x

Il segnale somma non ci interessa poiché noi dobbiamo lavorare ad una frequenza inferiore ad f_x.

La f_l0 è in funzione di t in quanto l’oscillatore fa variare la frequenza in funzione di t.

L’amplificatore a frequenza intermedia amplifica solo in una banda centrata alla frequenza intermedia ed allora si avrà una risposta quando:

| f_l0 (t) –f_x | = f_i +/- B/2

Questa quantità è modulata in frequenza perché f_l0 varia con continuità. Ci sono istanti di tempo in cui questa quantità cade fuori banda, istanti in cui comincia ad entrare in banda ed istanti in cui comincia ad uscire.

Dato che attraversiamo la banda dell’amplificatore, l’ampiezza della sua risposta va variando. Supponiamo che la f_l0 (t) va crescendo, amplificando le cose si ha la seguente situazione.

Man mano che passa il tempo f_l0 (t) cresce, f_x si considera costante , ed il valore assoluto diminuisce.

Si va pertanto da un valore f_i + B/2 ad un valore f_i - B/2.

Collegando l’uscita dell’amplificatore con un rivelatore ad inviluppo (cioè un pessimo convertitore di picco) si ottiene la forma d’onda .

Prendendo allora la parte positiva dell’inviluppo ottengo un segnale transitorio, se continuo a spazzolare ottengo un segnale periodico. Quest’ultimo non è altro che una replica della forma della banda passante dell’amplificatore ad f_i , posizionato però in un’ascissa dell’analizzatore di spettro che corrisponde al valore di f_l0 per il quale vale la relazione : | f_l0 (t) –f_x | = f_i +/- B/2.

Pertanto una sinusoide dà luogo ad una riga che non è altro che la banda passante statica dell’amplificatore a frequenza intermedia.

BATTIMENTO : Alternativo aumentare e diminuire dell’ampiezza di oscillazioni dovuto alla sovrapposizione di frequenze vicine.

Schema pag. 205

La sinusoide viene trasformata in una riga che è un transitorio di salita e di discesa che copre la banda passante statica dell’amplificatore a frequenza intermedia ogni volta che si ha la situazione

| f_l0 (t) –f_x | = f_i +/- B/2

La scansione di frequenza deve essere convenientemente maggiore della banda passante dell’amplificatore. A f_i - B/2 la banda è piccola rispetto la spazzolata vede una riga. Ho una sinusoide ad una ben definita frequenza .La frequenza dell’oscillatore locale è invece variabile nel tempo fra un valore massimo ed un valore minimo.

Sullo stesso asse posizioniamo l’ordinata che rappresenta f_x se da questa ordinata stacchiamo il segmento che rappresenta fi e gli colleghiamo intorno la su banda passante B,descriviamo graficamente il fenomeno.

Esaminando lo schema.

All’inizio è tutto fermo. All’istante t₀ si ha f_l0 (t) = f_x - B/2 allora l’amplificatore f_i inizia a rispondere

|f_l0 (t) –f_x | = f_i +/- B/2

Entriamo nell’amplificatore che avrà una certa banda passante da frequenze alte.

L’ampiezza da prima sarà piccola poi inizierà a crescere per poi decrescere. All’istante t₁ si ha il massimo della risposta: |f_l0 (t) –f_x | = f_i sono al centro della banda.

All’istante t₂ si esce dalla banda passante, nell’intervallo t_m si ha l’evoluzione della risposta salita e discesa, di cui noi prendiamo l’inviluppo

Il transitorio è tanto più simile ad una riga quanto più piccolo è il rapporto tra la banda passante dell’amplificatore a fi e l’intera dispersione f ,ossia quanto più piccolo è il rapporto tra tm e ts.

Grafico pag. 209

Se sull’asse dello schermo mando il dente di sega che ha provocato la scansione di frequenza f_l0 avrò una tensione triangolare quindi la posizione del transitorio è strettamente ed unicamente collegata al valore di f_x ; quindi se f_x si sposta su e giù la riga si sposta avanti e indietro. In questo modo si vede che lo schermo dell’A.S può essere tarato in frequenza i punti a sinistra corrispondono a f_l0 min i punti a destra a f_l0 max a mezzo della fi.

Ho supposto finora che la frequenza centrale dell’oscillatore fosse fissa.

L’A.S è quindi un ricevitore …eterodina (radioricevitore) con la differenza che l’oscillatore locale è a frequenza scandita invece che fissa.

I problemi che avevamo nell’oscilloscopio (x es. la sincronizzazione) vengono così moltiplicati perché devo considerare un ulteriore trasduzione legata alla frequenza. Infatti si deve andare inseguendo il segnale , così al momento dell’accensione non riesco a visualizzare nulla.

Oggi in effetti esistono sistemi di aggancio automatico che riescono ad acchiappare la frequenza che si deve inseguire.

Le prestazioni fondamentali dell’analizzatore di spettro sono:

Sensibilità: che è la minima ampiezza del segnale d’ingresso che da luogo ad una risposta discernibile

Risoluzione: che è la minima differenza di frequenza d’ingresso che da luogo a due risposte vicine ma ancora discernibili.

La fig. 53 vale per un segnale per un segnale che ha una sola frequenza d’ingresso.

Se invece in ingresso ho un segnale composto da due frequenze (per esempio ho un segnale che è la somma lineare di due segnali)dato che è modulato sia in ampiezza sia in frequenza sarà molto difficile da visualizzare nel dominio del tempo . Infatti nel dominio del tempo il segnale va variando mentre nel dominio della frequenza si può distinguere meglio.

Dal punto di vista della scansione di frequenza invece di ottenere un solo diagramma di risposta ne avrò 2, la seconda risposta sarà identica alla prima. Ho quindi 2 frequenze f_x1 ed f_x2 .

Se f_x2 tende ad f_x1 avrò una differenza di frequenza per la quale le due risposte risultano vicinissime ma ancora discernibili.

Fino ad arrivare ad un'unica riga per f_x1 = f_x2

Capacità di risposta a segnali di piccola ampiezza:

Il minimo scarto di frequenza tra due segnali applicati contemporaneamente applicati all’ingresso dell’A.S che da luogo a due risposte ancora discernibili.

L’analizzatore ideale dovrebbe scandire in qualunque campo di frequenza e segnali di qualunque ampiezza. Si hanno dei limiti, abbiamo appena visto cosa succede se due segnali sono a frequenze troppo vicine, in più se le due frequenze sono troppo lontane la risposta sarà limitata dalla capacità di modulare l’oscillatore locale.

La risoluzione nell’analizzatore di spettro è tanto migliore quanto minore è la banda dell’amplificatore fi, infatti minore è la banda occupata ,meno spazio occupa nella scansione ts .

Se voglio una buona sensibilità il guadagno dell’amplificatore a fi deve essere molto alto.

Dato che il prodotto del guadagno per l’ampiezza di banda da una costante , stringendo la banda posso aumentare il guadagno.

Sembrerebbe che la prestazione dell’analizzatore di spettro sia tanto migliore quanto più selettivo sia l’amplificatore . In realtà se la banda passante dell’amplificatore si restringe gradualmente ,il tm diventa progressivamente più piccolo: ci vorrà meno tempo affinché il segnale dell’oscillatore locale passi attraverso la banda passante.

Questo entra in conflitto con il tempo di risposta dell’amplificatore a frequenze intermedie.

La caratteristica fondamentale risulta: tr µ Q/w

Tr è tanto maggiore quanto più selettivo è il circuito.

Se aumento la selettività l’analizzatore andrà velocemente in crisi perché contemporaneamente a Tr aumenta Tm ( Tr è dell’ordine delle centinaia di m sec) , il rapporto fondamentale da considerare è Tr/Tm .

Qualitativamente se all’inizio Tr << Tm allora l’oscillatore locale passa lentamente per la banda passante, attraverso la frequenza intermedia ciò corrisponde ad accordare manualmente il circuito .Il circuito allora risponde con il suo funzionamento statico, per cui le varie ordinate della curva attenuata corrispondono alle ordinate dovute alla curva di risposta definita staticamente (dando una frequenza per volta).

Se l’amplificatore è reso più selettivo Tr/Tm cresce rapidamente perché Tr µ Q , ed aumenta, Tm µ B e diminuisce.

Una bassa B equivale a dire alto Q in un determinato campo di frequenze.

Ciò si ha in un qualunque sistema a scansione di frequenza : se voglio una buona selettività la scansione di frequenza diventa critica .

Se Ts diminuisce ( spazzola la frequenza in un tempo minore)diminuisce proporzionalmente Tm e considero invariati gli altri parametri, infatti:

Tm = B*Ts/F ma Tr = 0.7/B» 1/B

Tr/Tm = F/ TsB²

Se voglio che questo rapporto sia piccolo devo avere una piccola dispersione un lungo tempo di scansione ed una grande banda.

F, Ts, B sono caratteristiche dell’A.S in particolare F dipende dalla modulabilità dell’oscillatore locale (può essere variabile per la presenza del variatore: ci saranno diversi campi variazione utilizzando il comando frequency/div).

Quando Tr = Tm si accende una luce rossa che ci indica il limite del funzionamento.

Nel funzionamento statico la curva di risposta è una replica della curva di selettività dell’amplificatore con ampiezza proporzionale all’ampiezza di uscita.

Il fattore discriminante tra il comportamento statico e dinamico dell’analizzatore è dato da F/ TsB²

Se Tr << Tm ho un transitorio prevedibile in tutte in tutte le sue fasi con una scansione di frequenza tra un massimo ed un minimo.

Se questo rapporto tende a crescere ottengo la risposta dinamica che è più piccola, più aperta, più spostata. Aumentando la velocità e diminuendo il tempo di scansione la curva di risposta si schiaccia e si sposta.

Che la curva di risposta si abbassi è ragionevole in quanto la risposta dell’analizzatore è di tipo esponenziale (l’amplificatore dell’analizzatore è eccitato da una forma d’onda non a frequenza costante e risponde con un transitorio esponenziale). Se eccito il circuito con un Tm che diminuisce progressivamente (oppure con un Tr che aumenta) non lasciano il tempo all’amplificatore di salire al massimo

Che la risposta si allarghi è dovuto al fatto che la risposta dell’amplificatore dura più della domanda (bisogna dargli il tempo di salire e di scendere). In questo modo viene anche spostato il baricentro della curva rispetto l’intervallo di tempo nel quale possiamo attraversare la banda passante.

L’ampiezza dinamica è minore di quella statica

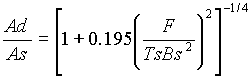ma si muove sull’altezza

la banda dinamica è maggiore di quella statica

schema pag 214

Non tutti i segnali possono essere visualizzati con l’A.S , ho un limite in termini di sensibilità e risoluzione. I segnali la cui ampiezza non supera un certo limite vengono annegati nel rumore dello strumento ,quindi non vengono rappresentati in maniera discernibile.

Non essendo i segnali che si presentano all’analizzatore solo di tipo sinusoidale ma anche di tipo complesso saranno maggiormente influenzati dal rumore :Il Rumore Bianco si presenta in termini di spettro come un fascio d’erba. Comunque non sono solo questi i problemi.

Sensibilità e risoluzione dipendono anche , in modo determinante dalla velocità di spazzolamento ciò può implicare che l’amplificatore intervenga con la sua curva di risposta dinamica anziché statica.

La curva di risposta statica si determina frequenza per frequenza: data una sollecitazione ad una determinata frequenza lasciamo il tempo all’amplificatore di raggiungere il regime su quella frequenza; ciò va bene per spazzolate lente oppure tempi lunghi.

Vogliamo esaminare un’onda complessa : onda a più frequenze di ampiezza diverse.

La più significativa tra le onde complesse è quella radaristica.

Lo spettro è centrato sulla frequenza della portante.

Ogni riga è l’inviluppo di un transitorio a frequenza intermedia

L’analizzatore di spettro in realtà non conserva l’informazione di fase (a differenza del volmetro vettoriale con cui ho una rivelazione sincrona) la rivelazione dell’inviluppo che da luogo alla riga sarà asincrona , in questo caso, e quindi lo spettro sarà tutto ad ordinate positive ( la fase non viene conservata).

E’ irrilevante sia il modo in cui la curva modulata in frequenza entra nella banda passante , sia la sua fase; importa solo l’inviluppo della curva di risposta.

1/t : distanza tra due zeri consecutivi t : durata dei pacchetti d’onda

1/T: distanza tra riga e riga T: intervallo tra i pacchetti d’onda

Suppongo di essere nelle condizioni per il quale è operativo il radar di avvistamento per oggetti metallici allora le condizioni affinché lo spettro possa essere rappresentato riga per riga sono:

f₀ > 1GHz (2-3-10)

t » 1m s

T » 1ms

L’intervallo tra impulso ed impulso deve essere grande per potere accettare l’impulso di ritorno con estrema precisione (devo ricordare che l’antenna è contemporaneamente di ricezione e trasmissione)

Esistono anche radar che sfruttano l’effetto Doppler.

Lo spettro che vogliamo rappresentare ha durata infinita e quindi non lo sappiamo analizzare. Voglio determinare la dispersione che possiamo accettare, come adeguata, per una forma di questo tipo.

Convenzionalmente considero che lo spettro sia adeguatamente conosciuto rappresentando il lobo centrale e due lobi laterali per parte(perché hanno a che fare con la banda passante)allora la dispersione accettabile sarà:

F= 6/t

Se la forma d’onda fosse modulata da impulsi perfettamente rettangolari e non vi fosse alcuna altra modulazione di frequenza all’interno dell’impulso , avrei uno spettro perfettamente simmetrico . In realtà, dato che il trasmettitore funziona in modo irregolare ho una non perfetta simmetria , ossia un’alterazione della banda passante ( un lobo si alza rispetto ai 3 db , ogni lobo ha in genere ampiezza minore di 3 db )

Per determinare la banda passante mi interessa il lobo centrale e i due lobi ad esso adiacenti, per essere certi che ci siano includo anche due lobi laterali per parte.

Distinguere righe poste ad una distanza 1/T si traduce in un limite sulla Bs .

L’ampiezza di due salite e discese è uguale alla banda passante statica .

Ogni transitorio è la replica della banda passante dell’amplificatore FI.

La banda passante è definita a metà potenza, non alla base.

Supponendo che le due righe siano incollate nella condizione limite di vicinanza nella quale non si ha sovrapposizione si vede che la Bs deve essere uguale ad un quarto di tutta l’ampiezza delle righe per avere un’adeguata risoluzione riga per riga, e per essere sicuri che alla base non si abbia sovrapposizione

Bs » 0.25/T

Possiamo metterci in condizione limite tra il fenomeno statico e dinamico:

Tr/Tm = F/ TsB² = 1 (1)

In queste condizioni si determina però una perdita di risoluzione e di ampiezza, ma è piccola.

Ho infatti individuato la Bs sapendo cosa sarà sufficiente, ossia la risoluzione effettiva sarà peggiore di quella relativa a Bs perché dipende anche dalla velocità di spazzata. Se considero la (1) mi metto nelle condizioni per cui il peggioramento che ci sarà non sia inaccettabile .

( nell’analizzatore posso scegliere diversi valori di Bs)

Dalla (1) e dai valori di T e t dati ,determino:

Ts=F/Bs² =96 sec

Anche la durata minima di Ts che da luogo ad un peggioramento è dell’ordine dei 100 sec ciò significa che per risolvere riga per riga lo spettro il tempo è troppo lungo . così rischiamo di perdere una delle caratteristiche fondamentali dell’analizzatore che mi permette di visualizzare un oscillogramma in tempo reale.

L’informazione sulla natura dello spettro deve essere molto veloce se no si rischia di danneggiare il tubo.

Possiamo generare segnali rappresentabili riga per riga giocando su T.

In questo caso in effetti non è necessario fare una risoluzione riga per riga , in quanto potrei misurare 1/T in un altro modo.

1/T = frequenza di ripetizione degli impulsi.

Analizzo lo spettro nel dominio della frequenza

In effetti mi interessa l’inviluppo dello spettro piuttosto che 1/T perché voglio determinare con precisione l’ampiezza dei lobi( le frequenze per cui lo spettro va a zero) per ricavare le informazioni sulla banda passante del segnale ( non legata alla singola riga ).

Lavorare con banda dell’amplificatore stretta è equivalente alla seguente operazione: suppongo di avere un cartoncino con un intaglio corrispondente alla banda e di farlo scorrere davanti al diagramma; distinguo le singole componenti se l’ampiezza è sufficientemente stretta . Bisogna andare lentamente altrimenti ‘impasto’ le righe.

Se utilizzo una finestra di frequenza più ampia mi porta ancora le righe ma riesco ad ottenere l’inviluppo. Posso così percepire l’informazione che viene dalla scolpitura in ampiezza dal pacchetto di righe che stanno dietro la finestra da me stabilita. Voglio esaminare l’intervallo di frequenza uguale ad 1/t con sufficiente finezza così da poter distinguere quando l’ampiezza è minima e massima. E’ ragionevole pensare che la Bs possa essere un decimo di 1/t ciò non è adeguato per una risoluzione riga per riga infatti con T = 1 msec e t = 1 m sec avrei mille righe in un lobo e dovrei visualizzare 6000 eventi sullo schermo. ( è già tanto se ne visualizzo 20 )

Voglio anche determinare il tipo di9 figura che si ottiene sullo schermo in queste condizioni.

La rappresentazione dello spettro avviene sempre per transitori indistinguibili dalle righe che si presentano quando risolviamo riga per riga .

Lo spettro si presenta sempre come un insieme di righe anche se risolviamo per inviluppo.

Bs = 0.25/T

Il tempo di risalita dell’amplificatore sarà:

1/Tr =0.25/T < 1/T allora Tr > T

1/T distanza in frequenza tra due impulsi

T tempo tra due impulsi

Quindi il tempo di risposta dell’analizzatore di spettro è maggiore del tempo impulso ed impulso; mentre si forma una riga passano circa quattro impulsi.

L’analizzatore non si accorge che la forma d’onda in ingresso è discontinua nel tempo perché la risposta si evolve al passare di molti impulsi . L’analizzatore funziona con continuità ed ha memoria del passato.

Bs = 0.1/t 1/Tr = Bs = 100/T allora Tr < T

1/t =1000* 1/T perché ho mille righe nell’intervallo 1/t per cui

t = T / 1000 allora Bs = 100 /T

L’analizzatore risponde con un transitorio per ogni impulso che arriva e si dimentica progressivamente di ciò che c’era prima. L’analizzatore funziona in modo impulsivo.

Nel diagramma in cui è rappresentata Vin in funzione di t si ha un onda radaristica :

l’evoluzione della f₀ nello scoppio è nascosta nello spessore del pennino . Lo spessore del pennino è circa 1/20 dell’intervallo tra lisca e lisca .

Essendo T/t » 20 abbiamo la possibilità di vedere nel tempo reale cosa succede con la risoluzione per riga e per inviluppo nello stesso tempo in cui si evolve il segnale

Vin

E’ il diagramma nel dominio del tempo della forma d’onda a radio

t frequenza modulata con impulsi rettangolari

nel diagramma superiore visualizzo la risoluzione per inviluppo, la scala dov’è rappresentato non ha importanza ( sono importanti la dispersione , la banda passante, ossia gli intervalli di frequenza, non è significativa f₀ che non compare nella trattazione).

Per ogni lobo ci sono 20 righe e 40 nel lobo centrale 6 lobi è la risoluzione adeguata.

Il diagramma è l’applicazione di figura 53 a pag. 209, quando invece di avere una frequenza d’ingresso ce ne sono tante si ha una variante in quanto nella fig. 53 si ha l’escursione di f_l0 e la riga si sviluppa nell’istante in cui fx – fi incontra f _l0 .

Avrei lo stesso effetto se invece di scandire f_l0 facessi il diagramma di f_l0 ± Fi (in questo caso in effetti dovrei considerare la somma)

Se impongo alla retta una traslazione verso l’alto non ho più bisogno di fare la sottrazione di fi e posso dire che la riga si forma nell’istante in cui la nuova retta incontra l’ordinata corrispondente ad fx, ottengo così la scansione in tempo reale di f_l0 + Fi

Nel diagramma inferiore ho una risoluzione riga per riga in cui ho la scansione di un solo lobo (30) righe).

Ho fissato Tm supponendo di lavorare riga per riga quindi Bs = 0.25/T = 1/Tr allora Tr = 4T , ed inoltre mi pongo in condizioni limite di funzionamento statico per cui Tr = Tm, allora Tm = 4T.

Tr è il tempo di risposta una riga si forma in un tempo di almeno 4T , lo zero del diagramma d’ingresso è arbitrario.

Partendo dallo zero del diagramma di Vin devo fare in modo che ciascun incrocio della retta che da la scansione di Ts non assuma un tempo di Tm affinché ci sia una salita ed una discesa.

La pendenza della retta di scansione deve essere sufficientemente bassa così da dare alla risposta il tempo di evolversi tra impulso ed impulso.

Se Tm >> T ho una risoluzione riga per riga.

Per descrivere un lobo ci vogliono 20 impulsi . Ho un ingresso impulsivo per cui per cui l’amplificatore è continuamente sollecitato da onde che danno luogo a continue salite e discese.

Ottengo una risposta continua che cambia in ampiezza ( l’analizzatore non si accorge di essere alimentato ad impulsi) . La risposta continua cambia in ampiezza perché cambia in ampiezza lo spettro , ossia la riga che di volta in volta diventa attiva. Se aumentassi la pendenza le righe si salderebbero l’una all’altra ( il limite si ha quando sono ancora distinguibili) Ho supposto che sia noto l’andamento della curva di risposta statica dell’amplificatore..

Se invece abbasso la pendenza le righe si allontanano in quanto c’è più tempo di quello necessario per formare una riga.

La condizione limite per fare saldare le righe è:

Tm = Tr = 4T.

Considero ora la risoluzione per inviluppo

In questo caso ho una risposta per ogni impulso , che comprende nel dominio del tempo 4 righe.

Posso lavorare con un dente di sega molto più pendente perché mi basta che siano distinti i pacchetti di righe e non le righe, soprattutto quelli che cadono nei punti tipici.

Prima comandava la riga di frequenza in questo caso comanda l’impulso infatti si vede che ogni riga ha la stessa posizione temporale di un impulso di sopra.

Ho una risposta la cui ampiezza corrisponde all’inviluppo del pezzetto di spettro che in quel momento è chiamato in causa. Le varie ampiezze cambiano perché varia f_l0 anche se gli impulsi sono tutti uguali.

Supponendo di scegliere una scala opportuna posso fare in modo che i 2 spettri (risoluzione per righe ed inviluppo) mi appaiano ugualmente separati sullo schermo dell’oscilloscopio.

Posso però distinguere le due risoluzioni in questo modo:

Se cambio la pendenza quando lo spettro è risolto riga per riga , il numero di righe non può cambiare perché in ogni caso devo avere una risposta per ogni riga ( le righe potranno avvicinarsi oppure allontanarsi per cui lo spettro impiega più tempo per fermarsi).

Nello spettro risolto per inviluppo cambia il numero di righe ,perché cambia il numero di impulsi catturati per ogni spazzolata dato che c’è una risposta ( una riga ) non per ogni frequenza ma per ogni impulso (spettro ad impulso ). All’aumentare della pendenza lo spettro sarà più denso e l’inviluppo sarà meglio definito ( aumenta il numero di righe).

In termini dell’informazione che voglio ottenere ossia in termini dell’individuazione del massimo o del minimo dei lobi dovrò operare la scelta migliore tra le due risoluzioni.

Nella risoluzione per inviluppo

Ts = F/ Bs² Tm = B* Ts /F

Dove Ts è il tempo minimo in cui lo spettro viene risolto staticamente , nel quale l’amplificatore non viene spazzolato troppo velocemente Tr = Tm = 1

Tr e Tm dipendono solo dall’analizzatore di spettro e non dalla forma d’onda da visualizzare e possono essere più o meno adeguati alla stessa forma d’onda .

Bs minima è la scelta fatta sull’analizzatore ( se Bs è grande ottengo un Ts minore staticamente).

Se al posto di Bs = 0.25/T metto Bs = 0.1/ T che è maggiore ,allora il tempo minimo per scandire lo spettro in condizioni statiche, Ts, diventa minore , dell’ordine dei 100 m sec.

Cambiare Bs implica Ts grande nella risoluzione riga per riga ( Bs minima ed F che non cambia) , e implica un Ts piccolo nella risoluzione per inviluppo.

Pag. 228

Se abbiamo una sola frequenza io ho una sola riga sullo schermo ,ciò non sempre è vero in quanto sullo schermo potrei non avere una riga per ogni frequenza .

Posso ricondurmi però a questo caso facendo in modo che l’analizzatore funzioni in modo statico .

Il problema è dato dal fatto che l’analizzatore funziona in modo non lineare, se applico un segnale ad una determinata frequenza in uscita avrò più frequenze ,.Anche se ho una sola frequenza avrò più righe.

Finora abbiamo supposto che il mescolatore abbia una caratteristica perfettamente quadratica quindi per ogni frequenza dell’oscillatore locale avrò la somma e la differenza (catturo la differenza con l’amplificatore).

Se la forma della curva di trasferimento non è quadratica in uscita avrò dei prodotti di modulazione di ordine superiore, ossia invece di ottenere semplicemente somme e differenze di frequenza ottengo una combinazione lineare del tipo

m f_l0 ± n fx m ed n interi

anche se in realtà potrei escludere le somme in quanto stanno in un campo di frequenza troppo alto per essere visualizzata, se scelgo fi più bassa della più bassa frequenza dell’oscillatore locale.

Quindi ogni volta che si ha la condizione:

|m f_l0 ± n fx| = Fi ± B/2

l’analizzatore risponde perché centra qualcosa nella banda passante .

Per ovviare a ciò dovrei rendere perfettamente quadratica la caratteristica del mescolatore . Di solito si ricorre a mescolatori a diodi perché il diodo ha una caratteristica che si avvicina a quella quadratica , nel primo tratto.

Otterrò sempre dei prodotti di modulazione però se progetto bene il mescolatore, mi aspetto che questi abbiano ampiezza molto inferiore a quella che compete il segnale che mi interessa : | f_l0 - fx|

Se la caratteristica è quasi quadratica le componenti somma e sottrazione hanno la massima ampiezza mentre le altre componenti avranno ampiezza molto più piccola in quanto sono dovute a deviazioni della curva quadratica ( progettando bene le deviazioni devono essere molto piccole).

Se ho segnali di ampiezza notevole, tanto notevole da doverli attenuare per non sovraccaricare il circuito di ingresso ,il problema non si pone. Infatti se i segnali sono dell’ordine del fondoscala posso ritenere che le risposte siano piccole nei confronti della massima ampiezza che io posso realizzare, vedere sullo schermo.

Il problema si ha quando si hanno segnali che contengono componenti di tutte le ampiezze per esempio se ho un segnale di tipo radaristico . La presenza di componenti armoniche limitano il campo di ampiezza spazzabile.

Oggi riusciamo ad esplorare un campo che è (-120 –140 dbm) (il nostro analizzatore (-70 - -140)

Il rapporto tra la massima ampiezza ( fondoscala) discernibile sullo schermo e la minima ampiezza fissata dalle risposte spurie; questo rapporto è fornito dal costruttore, maggiore è il numero ottenuto migliore è l’analizzatore.

A causa delle risposte spurie non posso vedere contemporaneamente segnali di piccola e di grande ampiezza.

Quando ho uno spettro composto da più frequenze , quindi sono interessato a leggere diversi livelli stabilisco un livello in db