Chapter 2 Section 5
Quadrilaterals
A Quadrilateral is a four-sided closed plane
figure.
Different types of Quadrilaterals:
|
Square |
Quadrilateral
with opposite sides parallel, all four sides congruent, and with four 90
degree angles |
|
Rectangle |
Quadrilateral
with opposite sides parallel and congruent with four 90 degree angles |
|
Parallelogram |
Quadrilateral
with opposite sides parallel |
|
Rhombus |
Quadrilateral
with opposite sides parallel and all four sides congruent |
|
Trapezoid |
A
quadrilateral with exactly one pair of parallel lines |
|
Isosceles trapezoid |
A
trapezoid with one pair of parallel line connected by two congruent lines |
|
Kite |
Convex
quadrilateral with no parallel sides, but two sets of adjacent congruent
sides |
|
Deltoid |
Concave
quadrilateral with no parallel sides, but two sets of adjacent congruent
sides |
|
Trapezium |
Quadrilateral
with no parallel sides |
Pictures of these quadrilaterals can be seen
at Quadrilateral-Wikipedia
Parallelogram: a quadrilateral with both pairs of opposite
side parallel
A parallelogram is named by naming its four
vertices in any order.
Our example is named ABCD or CDBA
Opposite side of a parallelogram are
congruent.
·
In our example side AC is congruent to side DB and side CD is congruent
to side BA.
Opposite angles of a parallelogram are
congruent.
·
In our example angle ACD is congruent to angle DBA and angle CDB is
congruent to angle BAC.
Parallelograms can be classified three ways
A rectangle is an equiangular parallelogram
A rhombus is an equilateral parallelogram
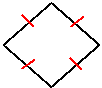
A square is a regular parallelogram
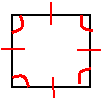
The diagonals of a parallelogram bisect each
other.
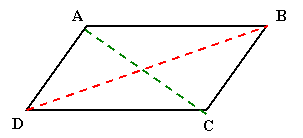
If ABCD is a parallelogram, then AC bisects
BD and BD bisects AC