< Previous | Home | Up | Table of Contents | Next >
Soft Uploading:
Tasks include:
There is a plethora of statistical and machine learning tools that may be applicable.
The compartmental model is the most realistic and accurate way to model a biological neuron. The assumption is that all relevant information processing can be emulated with this model. It should also serve as the yardstick against which other models' performance should be compared.
The following is adapted from Methods in Neuronal Modeling [Koch & Segev 1999] and Theoretical Neuroscience [Dayan & Abbott 2001].
Each compartment is assumed to be isopotential and spatially uniform in its properties. The mathematical formulation is a set of ordinary differential equations, one for each compartment. Each equation is derived from Kirchhoff's current law (ie, in each compartment, j, the net current through the membrane, im, must equal the longitudinal current that enters that compartment minus the longitudinal current that leaves it):
![]() .
.
The membrane current im (for the j-th compartment) can be expressed as:
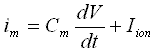 .
.
Applying Ohm's law and combining the above equations:
 .
.
Where the r's are axial resistances between compartments. The transcient solution to this equation depends critically on the description of Iion, which is the sum of 3 components:
List of modeling parameters: 
|
symbol |
meaning |
estimated number of measurements needed |
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Some simpler models are as follows:
Simple Threshold Units
One of the simplest model of a biological neuron is the threshold unit, where synaptic inputs are given by X[i] and synaptic strengths are given by W[i]. The neuron computes its output using

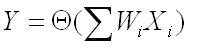
where Θ is a threshold function (binary, linear, sigmoidal, etc). Denote the number of synapses as n = #(synapses). Number of parameters in this model Nmodel = n.
An algorithm similar to the Perceptron learning algorithm is used to train this model:

Without optimization, number of multiplications per input trial = 2n. Time complexity ~ O(2N • n) where N = number of steps.
Simple Spike Response Model (SRM0)
The SRM0 model has n parameters.

η represents the action potential, t^ is the last firing time of the neuron, ε is the function for a single PSP, t(f) is the firing of each pre-synapse.
Simple Dendritic Tree Model
A more detailed level is to represent the dendritic tree explicitly. Assume dendrite diameters and ion-channel distributions etc can be statistically derived from the neuron's branching pattern. The tree structure can be represented by the branching pattern b[i] = number of branch points at each node i. Then each segment of the dendrite can be represented by L[i,j] as shown in the figure. Each synaptic weight W is given by a local synaptic strength (w) plus the synapes' position (α) on the segment where it belongs (L[i,j]). The final value of W (as in the product W • X) is a function of (w, α, L, b) which can be calculated using the compartmental model of dendrites.
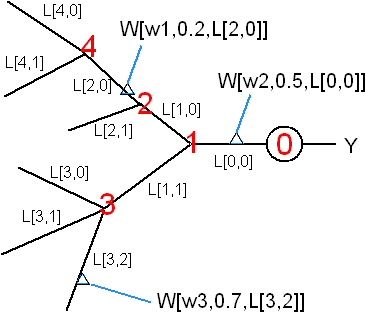
![]()
Total number of parameters in this model (excluding information about the branching pattern) Nmodel = 2n + #(dendritic segments) where n = #(synapses). If α (synapse position within a segment) can be absorbed into w (local synaptic strength), then 2n can be reduced to n. This model may be superior to the Sigma-Pi model in that it has fewer parameters and the parameters have physical meaning.
The general problem is known as adaptive modeling, ie the (semi-)automatic generation of models that approximate the compartmental models.
Reduction of dimensionality
P = set of physical parameters including: ion channel distribution and density, dendritic/axonal morphology, characteristics of voltage-gated ion channels, synaptic parameters (eg release probability or more elaborate details) etc etc...
The neuron's output is given by
Y(t) := Compartmental_Model(P, {Xt})
which we want to transform into
Y(t) := f(Q, {Xt})
where Q has fewer independent parameters. This involves 2 things: 1) automated experiments to determine all elements in P (parameter fitting / adaptive modeling); 2) optimization to simplify P to Q.
May be possible only after the optimal neuron models are obtained.
Time required for convergence depends on:
How to increase the rate of convergence? Increasing the resolution of (sub-threshold) voltage recording and the resolution in time domain may help.
Convergence fails after some time
For a simple binary threshold unit, the perceptron training algorithm gives the typical performance as follows:



As shown, the model's convergence flattens out like a pancake (with a residual value above zero) after an initial region of high performance. This is because random inputs are becoming less and less likely to fall on the error gap between the model and the real neuron. (The model is a hyperplane that divides the synaptic space which is an n-dimensional hypercube). Only inputs that fall on that gap can contribute to convergence.
{ is there any hope that sub-threshold and spike timing info can help this? depends on exact form of dendritic integration... whether it preserves voltage and timing... degree to which it preserves or blurs... therefore parameter fitting; we know... voltage is attenuated... which means it is close to noise... 1-10K synapses compressed to a space of 5-10mV + noise... each is down to ~1.4μV, timing is also blurred... extent of blur ? times... plus the number of parameters explode... but Perceptron is O(Nn)... increased parameters to such a point as to be unfeasible... because all parameters have to be trained... rate determining thing is probably background firing rate... }
< Previous | Home | Up | Table of Contents | Next >
14/Feb/2004 Yan King Yin