DERIVATION.

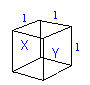
We consider a single particle in a cube, travleing in a straight line between two faces (X and Y), each time it hits either face, from the assumptions, it undergoes a perfectly elastic collision, and hence its change of momentum is m c to -m c, a total change of 2 m c. Force is equal to rate of change of momentum, so we now need to find how frequently it hits the side. It is traveling a velocity u and the cube is l accross, so there it travels 2 l before hitting the face again, this means it takes ^2l / _u. This makes the force on one side equal to m c² / _L, and the force per unit area (pressure) equal to m c² / _L3. Extending this for N molecules p = N m c^2' / _L3, where c^2' is the average of the sqaure of velocity. But N m / _L3 = ρ (density). Assuming that when the velocities of the molecules are divided into their perpendicular components the oscillations are evenly distributed amoung the 3 planes the pressure of a gas will be equal to a third of the density multiplied by the mean of the square of the velocity. i.e.

Notes:

• The distinction between the (mean velocity) squared and the mean of the squared velocity.